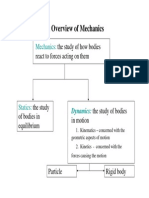
Chapter Two

Kinematics of particles
Introduction
Kinematics: is the branch of dynamics which describes
the motion of bodies without reference to the
forces that either causes the motion or are
generated as a result of the motion.
Kinematics is often referred to as the geometry of
motion
Examples of kinematics problems that engage
the attention of engineers.
The design of cams, gears, linkages, and other
machine elements to control or produce
certain desired motions, and
The calculation of flight trajectory for
aircraft, rockets and spacecraft.
If the particle is confined to a specified path, as with a bead
sliding along a fixed wire, its motion is said to be Constrained.
Example 1. - A small rock tied to the end of a string and whirled in a
circle undergoes constrained motion until the string
breaks
If there are no physical guides, the motion is
said to be unconstrained.
Example 2. - Airplane, rocket
The position of particle P at any time t can be
described by specifying its:
- Rectangular coordinates; X,Y,Z
- Cylindrical coordinates; r,,z
- Spherical coordinates; R, ,
- Also described by measurements along the tangent
t and normal n to the curve(path variable).
The motion of particles(or rigid bodies) may be
described by using coordinates measured from
fixed reference axis (absolute motion analysis)
or by using coordinates measured from moving
reference axis (relative motion analysis).
Rectilinear motion
Is a motion in which a particle moving along a
straight line(one-dimensional motion)
Consider a particle P moving along a straight
line.
Average velocity: for the time interval t, it is defined as
the ratio of the displacement s to the time interval t.
2.1
As t becomes smaller and approaches zero in the limit,
the average velocity approaches the instantaneous velocity
of the particle.
2.2
t
s
= V
av

= =

= = S
dt
ds
t
s
t t 0
av
0
lim V lim V
Average acceleration
For the time interval t, it is defined as the ratio of the
change in velocity v to the time interval t.
2.3
Instantaneous acceleration
2.4(a)
2.4(b)
t
v
a
av

= =

= v
dt
dv
t
v
t 0
lim a
s
dt
s d
dt
ds
dt
d
dt
dv
t
v
t
= =
|
.
|

\
|
= =

=

2
2
0
lim a
Note:-The acceleration is positive or negative
depending on whether the velocity increasing
or decreasing.
Considering equation 2.2 and 2.4(a) , we have
ds s s d s
s
s d
s
ds
dt
ads vdv
a
dv

= = =
=
= =
v
ds
dt
General representation of Relationship
among s, v, a & t.
1. Graph of s Vs t
By constructing tangent to the curve at any time t,
we obtain the slope, which is the velocity v=ds/dt
2. Graph of v Vs t
The slope dv/dt of the v-t curve at any instant gives the acceleration at
that instant.
The area under the v-t curve during time dt is vdt which is the
displacement ds
The area under the v-t curve is the net
displacement of the particle during the
interval from t1 to t2.
(area under v-t curve )

=
2
1
2
1
s
s
t
t
vdt ds
=
2 2
s s
3. Graph of a vs t
The area under the a-t curve during time dt is the net change in
velocity of the particle between t1 and t2.
v2 - v1=(area under a-t curve)

=
2
1
2
1
v
v
t
t
adt dv
4. Graph of a Vs s
The net area under the curve b/n position
coordinates s1 and s2 is
(areas under a-s curve)

=
2
1
2
1
v
v
s
s
ads vdv
= ) (
2
1
2
1
2
2
v v
5. Graph of v vs. s
ds CB vdv
v
CB
ds
dv
v
CB
ds
dv
= =
= =
1
tan
The graphical representations described are useful for:-
visualizing the relationships among the several motion quantities.
approximating results by graphical integration or differentiation
when a lack of knowledge of the matimatical relationship prevents
its expression as an explicit mathematical function .
experimental data and motions that involve discontinuous
relationship b/n variables.
Methods for determining the
velocity and displacement
functions
a) Constant acceleration, (a=const.)
- boundary conditions
at t=0 , s=s0 and v=v0
using integrating
dv adt
dt
dv
a = =
at v v
at v v adt dv
o
t
o
v
v
o
+ =
= =

0
Using
Using
( )
) s a(s v v
s s a
v v
as
v
ads vdv ads vdv
o
o
o
s
s
s
v
v
s
o
v
o
v
o o
0
2
2
2
2 2
2
2 2
+ =
=

=
= =

2
2
2
1
2
) (
0
at t v s s
at
t v s s
dt at v ds
vdt ds
dt
ds
v
o o
o o
t
o
o
s
s
+ + =
+ =
+ =
= =

These relations are necessarily restricted
to the special case where the acceleration
is constant.
The integration limits depend on the initial
and final conditions and for a given
problem may be different from those used
here.
Typically, conditions of motion are specified by the type
of acceleration experienced by the particle.
Determination of velocity and position requires two
successive integrations.
Three classes of motion may be defined for:
- acceleration given as a function of time, a = f(t)
- acceleration given as a function of position, a = f(x)
- acceleration given as a function of velocity, a = f(v)
b) Acceleration given as a function of time, a=f(t)
( ) ( )
( )
( ) ( ) ( )
( ) ( )
( )
( ) ( ) ( )


= = = =
= = = = =
t t t x
x
t t t v
v
dt t v x t x dt t v dx dt t v dx t v
dt
dx
dt t f v t v dt t f dv dt t f dv t f a
dt
dv
0
0
0
0
0
0
0
0
c) Acceleration given as a function of position, a = f(x)
( )
( ) ( ) ( )

= = =
= = = = =
x
x
x
x
v
v
dx x f v v dx x f dv v dx x f dv v
x f
dx
dv
v a
dt
dv
a
v
dx
dt
dt
dx
v
0 0 0
2
0 2
1
2
2
1
or or
d) Acceleration given as a function of velocity, a = f(v)
( )
( ) ( )
( )
( )
( ) ( )
( )

=
= = = =
=
= = = =
v
v
v
v
x
x
v
v
t v
v
v f
dv v
x x
v f
dv v
dx
v f
dv v
dx v f a
dx
dv
v
t
v f
dv
dt
v f
dv
dt
v f
dv
v f a
dt
dv
0
0 0
0
0
0
0
Example 1
Consider a particle moving in a straight line, and assuming
that its position is defined by the equation
Where, t is express in seconds and s is in meters.
Determine the velocity and acceleration of the particles at
any time t
3 2
6 t t s =
Example 2
The acceleration of a particle is given by ,
where a is in meters per second
squared and t is in seconds. Determine the
velocity and displacement as function time. The
initial displacement at t=0 is s
o
=-5m, and the
initial velocity is v
o
=30m/s.
30 4 = t a
Example 1
The position of a particle which moves along a straight
line is defined by the relation
,where x is expressed in m and t in
second.
Determine:
a) The time at which the velocity will be zero.
b) The position and distance traveled by the particle at
that time.
c) The acceleration of the particle at that time.
d) The distance traveled by the particle between 4s and
6s.
40 15 6
2 3
+ = t t t x
Example 2
A particle moves in a straight line with velocity
shown in the figure. Knowing that x=-12m at
t=0
Draw the a-t and x-t graphs, and
Determine:
a) The total distance traveled by the particle when
t=12s.
b) The two values of t for which the particle passes
the origin.
c) The max. value of the position coordinate of the
particle.
d) The value of t for which the particle is at a
distance of 15m from the origin.
Example 3
the rocket car starts from rest and
subjected to a constant acceleration of
until t=15sec. The brakes are then
applied which causes a decelerated at a
rate shown in the figure until the car
stops. Determine the max. speed of the
car and the time when the car stops.
2
6m/s a =
Example 4
A motorcycle patrolman starts from rest at A two seconds
after a car, speeding at the constant rate of 120km/h,
passes point A. if the patrolman accelerate at the rate of
6m/s
2
until he reaches his maximum permissible speed of
150km/h, which he maintains, calculate the distance s
from point A to the point at which he overtakes the car.
Example 5
The preliminary design for a rapid transient system calls
for the train velocity to vary with time as shown in the
plot as the train runs the 3.2km between stations A and B.
The slopes of the cubic transition curves(which are of
form a+bt+ct
2
+dt
3
) are zero at the end points.
Determine the total run time t between the stations and
the maximum acceleration.
Plane curvilinear motion
Curvilinear motion of a particle
When a particle moves along a curve other
than a straight line, we say that the particle
is in curvilinear motion.
Plane curvilinear motion
The analysis of motion of a particle along a
curved path that lies on a single plane.
Consider the continuous motion of a particle along a
plane curve.
- At time t, the particle is at position P, which is
located by the position vector r measured from
some convenient fixed origin o.
- At time , the particle is at P located by the
position vector .
- The vector r joining p and p represents the
change in the position vector during the time
interval t (displacement) .
t t +
r r +
The distance traveled by the particle as it
moves along the path from P to P is the scalar
length s measured along the path.
The displacement of the particle, that
represents the vector change of position and is
clearly independent of the choice of origin.
The average velocity of the
particle between P and P
defined as:
which is a vector whose
direction is that of .
The instantaneous velocity,
t
r
V
av

=
r
v

= =

= = r
dt
r d
t
r
v v
t
av
t
lim lim
0 0
Note: As t approaches zero, the direction of
approaches to the tangent of the path. Hence the
velocity V is always a vector tangent to the path.
The derivative of a vector
is itself a vector having both
a magnitude and a direction.
r

= = = s
dt
ds
v v
Note: there is a clear distinction between the
magnitude of the derivative and the derivative
of the magnitude.
- The magnitude of the derivative.
- The derivative of the magnitude
speed v v r
dt
r d
= = =

= = r
dt
dr
dt
r d
- The rate at which the length of the
position vector is changing.
The magnitude of the vector v is called the
speed of the particle.
t
s
t
pp
v
t t

=

lim lim
0
'
0
dt
ds
v =

r
r
Consider the following figure
- let the velocity at p be
- let the velocity at p be
v
v

Let us draw both vectors v and v from the same

origin o. The vector v joining Q and Q
represents the change in the velocity of the
particle during the time interval t.
v=v+v
Average acceleration, of the particle between
P and P is defined as , which is a vector and
whose direction is that of v.
Instantaneous acceleration,
t
v

t
v
a
av

=
a

= = =

= = r v
dt
v d
t
v
a a
av
lim lim
Note: The direction of the acceleration of a
particle in curvilinear motion is neither
tangent to the path nor normal to the
path.
Suppose we take the set of velocity vectors and trace
out a continuous curve; such a curve is called a
hodograph.
The acceleration vector is tangent to the hodograph,
but this does not produce vectors tangent to the path
of the particle.
Rectangular co-ordinates (x-y-z)
This is particularly useful for describing
motions where the x,y and z-components of
acceleration are independently generated.
When the position of a particle P is defined at
any instant by its rectangular coordinate x,y
and z, it is convenient to resolve the velocity
v and the acceleration a of the particle into
rectangular components.
Resolving the position vector r of the particle
into rectangular components,
r=xi+yj+zk
Differentiating
)

( k z j y i x
dt
d
dt
r d
v + + = =

k z j y i x v

+ + =
All of the following are equivalent:
)

( k z j y i x
dt
d
dt
r d
v + + = =

k
dt
dz
j
dt
dy
i
dt
dx

+ + =
k v j v i v
z y x

+ + =
k z j y i x

+ + =
Since the speed is defined as the magnitude of the velocity, we have:
2 2 2
z y x
v v v v + + =
Similarly,
)

( k v j v i v
dt
d
dt
v d
a
z y x
+ + = =

k
dt
dv
j
dt
dv
i
dt
dv
z
y
x

+ + =
k v j v i v
z y x

+ + =
k z j y i x

+ + =
The magnitude of the acceleration vector is:
2 2 2
z y x
a a a a + + =
From the above equations that the scalar
components of the velocity and acceleration
are

=
=
x a
x v
x
x

=
=
y a
y v
y
y

=
=
z a
z v
z
z
The use of rectangular components to
describe the position, the velocity and the
acceleration of a particle is particularly
effective when the component a
x
of the
acceleration depends only upon t,x and/or v
x,
similarly for a
y
and a
z.
The motion of the particle in the x direction,
its motion in the y direction, and its motion in
the z direction can be considered separately.
Projectile motion
An important application of two dimensional
kinematic theory is the problem of projectile
motion.
Assumptions
Neglect the aerodynamic drag, the earth
curvature and rotation,
The altitude range is so small enough so
that the acceleration due to gravity can be
considered constant, therefore;
Rectangular coordinates are useful for the
trajectory analysis.
In the case of the motion of a projectile, it
can be shown that the components of the
acceleration are
0 = =

x a
x
g y a
y
= =

0 = =

z a
z
Boundary conditions
at t=0 ; x=x
0
,y=y
0
; vx=vxo and vy=vy0
Position
Velocity
t v z z
gt t v y y
t v x x
o z o
y
x
+ =
+ =
+ =
2
0 0
0 0
2
1
) ( 2
2 2
0
0
o yo y
zo z
y y
x x
y y g v v
v z v
gt v y v
v x v
=
= =
= =
= =

In all these expressions,

the subscript zero
denotes initial conditions
But for two dimensional motion of the projectile,
2
0 0
0 0
2
1
gt t v y y
t v x x
y
x
+ =
+ =
) ( 2
2 2
0
0
o yo y
y y
x x
y y g v v
gt v y v
v x v
=
= =
= =

If the projectile is fired from the origin O, we have

x
o
=y
o
=0 and the equation of motion reduced to
2
0
0
2
1
gt t v y
t v x
y
x
=
=
gt v v
v v
y y
x x
=
=
0
0
Example
A projectile is fired from the edge of a 150m cliff with an initial
velocity of 180m/s at angle of 30
0
with the horizontal. Neglect
air resistance, find
a) the horizontal distance from gun to the point where the
projectile strikes the ground.
b) the greatest elevation above the ground reached by the
projectile.
Example
A projectile is launched from point A with the
initial conditions shown in the figure.
Determine the slant distance s that locates the
point B of impact and calculate the time of
flight.
Example
The muzzle velocity of a long-range rifle at A is
u=400m/s. Determine the two angles of
elevation that will permit the projectile to
hit the mountain target B.
Curvilinear motion
Normal and tangential coordinates
Normal and tangential coordinate
When a particle moves along a curved path, it
is sometimes convenient to describe its
motion using coordinates other than
Cartesian.
When the path of motion is known, normal (n)
and tangential (t) coordinates are often used.
They are path variables, which are
measurements made along the tangent t and
normal n to the path of the particle.
The coordinates are considered to move along
the path with the particle.
In the n-t coordinate system, the origin is
located on the particle (the origin moves with
the particle).
The t-axis is tangent to the path (curve) at
the instant considered, positive in the
direction of the particles motion.
The n-axis is perpendicular to the t-axis with
the positive direction toward the center of
curvature of the curve.
The coordinate n and t will now be used to
describe the velocity v and acceleration a.
Similarly to the unit vectors i and
j introduced for rectangular
coordinate system, unit vectors
for t-n coordinate system can be
used.
For this purpose we introduce
unit vector
e
t
in the t-direction
e
n
in the n-direction.
e
t
- directed toward the direction of
motion.
e
n
-directed toward the center of curvature
of the path.
During the differential
increment of time dt, the
particle moves a differential
distance ds along the curve
from A to A.
With the radius of curvature
of the path at this position
designated by , we see that
ds = d
velocity
The magnitude of the velocity is:-
Since it is unnecessary to consider the
differential change in between A and A,
dt
d
dt
d
dt
ds
v v

= = = =

) 1 ....( .......... ..........

t t
e e v v

= =
Acceleration
The acceleration a of the particle was defined
by:
Now differentiate the velocity by applying the
ordinary rule (chain rule) for the differentiation of
the product of a scalar and a vector.
( )
t
ve
dt
d
dt
dv
a = =

( )

+ =
+ = = =
t t
t
t t
e v e v a
dt
de
v e
dt
dv
ve
dt
d
dt
dv
a

Where the unit vector e

t
now has a derivative
because its direction changes.
. . . . . . . . . . . (1)
dt
de
v e
dt
dv
a
t
t
+ =

To find the derivative of consider the

following figure
Using vector addition
e
t
= e
t
+ e
t
Since the magnitude
| e
t
|= | e
t
| = 1
dt
de
t
The magnitude of e
t
| e
t
|= 2 sin /2
Dividing both sides by
As 0, is tangent to the path;i.e,
perpendicular to e
t
.

2
sin 2
t
e

t
e
Taking the limit as 0
The vector obtained in the limit is a unit
vector along the normal to the path of the
particle.
1
2
2
sin
lim lim
0 0
=

t
e
1 lim
0
= =

d
de e
t t
But
Dividing both sides by dt
But d = ds/
Then
n t
t
n
n
t
e d de
d
de
e
e
d
de
.
. 1

= =
=
n
t
e
dt
d
dt
de
.

=
n
t
n
t
e
v
dt
de
e
dt
ds
dt
de

= = .
1
Equation (1) becomes
We can write
where, and
t n t
t
e
dt
dv
e
v
a e
dt
dv
dt
de
v a . .
2
+ = + =

t t n n
e a e a a + =
2 2

= =

v
a
n

= = v a
t
2 2
t n
a a a a + = =
Note:
a
n
is always directed towards the center of
curvature of the path.
a
t
is directed towards the positive t-direction of
the motion if the speed v is increasing and
towards the negative t-direction if the speed v is
decreasing.
At the inflection point in the curve, the normal
acceleration, goes to zero since becomes
infinity.

2
v
Special case of motion
Circular motion
but =r and

2
v
a
n
=

= r v
2

= r a
n
n t
t
t
e r e r a
r a
dt
d
r r
dt
d
dt
dv
a
2

+ =
=
=
|
.
|

\
|
= =

The particle moves along a path expressed as

y = f(x). The radius of curvature, , at any
point on the path can be calculated from
2
2
2
3
2
) ( 1
dx
y d
dx
dy
xy
)
`

+
=
APPLICATIONS
Cars traveling along a
clover-leaf interchange
experience an acceleration
due to a change in speed as
well as due to a change in
direction of the velocity.
Example 1
Starting from rest, a motorboat
travels around a circular path of
r = 50 m at a speed that increases
with time, v = (0.2 t
2
) m/s.
Find the magnitudes of the boats
velocity and acceleration at the
instant t = 3 s.
Example 2
A jet plane travels along a vertical
parabolic path defined by the equation
y = 0. 4x
2
. At point A, the jet has a
speed of 200 m/s, which is increasing at
the rate of 0. 8 m/s
2
. Find the magnitude
of the planes acceleration when it is at
point A.
Example 3
A race traveling at a speed of 250km/h on the
straightway applies his brakes at point A and
reduce his speed at a uniform rate to 200km/h at
C in a distance of 300m.
Calculate the magnitude of the total acceleration
of the race car an instant after it passes point B.
Example 4
The motion of pin A in the fixed circular slot
is controlled by a guide B, which is being
elevated by its lead screw with a constant
upward velocity v
o
=2m/s for the interval of
its motion.
Calculate both the normal and tangential
components of acceleration of pin A as it
passes the position for which .
Curvilinear motion
Polar coordinate system (r- )
Polar coordinate(r- )
The third description for plane curvilinear
motion.
Where the particle is located by the radial
distance r from a fixed pole and by an angular
measurement to the radial line.
Polar coordinates are particularly useful when a
motion is constrained through the control of a
radial distance and an angular position,
or when an unconstrained motion is observed by
measurements of a radial distance and an angular
position.
An arbitrary fixed line,
such as the x-axis, is
used as a reference for
the measurement .
Unit vectors e
r
and e

are established in the

positive r and
directions, respectively.
The position vector to the particle at A has a
magnitude equal to the radial distance r and a
direction specified by the unit vector e
r
.
We express the location of the particle at A by
the vector
r
e r. r

=
r

Velocity
The velocity is obtained by differentiating the vector r.
Where the unit vector e
r
now has a derivative because
its direction changes.
We obtain the derivation in exactly the same way that
we derived for e
t
.

+ =
+ = = =
r r
r
r
r
e r e r v
dt
e d
r e
dt
dr
dt
e dr
dt
r d
v

. .
.
To find the derivative of consider the
following figure
Using vector addition
e
r
= e
r
+ e
r
e

= e

+ e

Since the magnitude

|e
r
| = |e
r
| = |e

|= |e

| = 1
dt
de
r
The magnitude of e
r
and e

| e
r
|= |e

| =2 sin /2
Dividing both sides by
As 0, is perpendicular to e
r
.

2
sin 2
e e
r

r
e
Note: As 0,
1. is directed towards
the positive e

direction.
2. is directed towards
the negative e
r
direction.
Then,

r
e

e
1
2
2
sin
lim lim lim
0 0 0
=

e e
r
Therefore;
1 lim
1 lim
0
0
=

de e
de e
r r
r r r
r
r
e d de e e
d
de
e d de e e
d
de


. . 1
. . 1

= = =
= = =
Dividing both sides by dt, we have
Therefore the velocity equation becomes;
r r
r r
e
dt
e d
e
dt
d
dt
e d
e
dt
e d
e
dt
d
dt
e d

.
.

= =
= =

e r e r
dt
e d
r e
dt
dr
v
r
r
r

+ = + = . .
Where
and

= r v
r

. r v
|
|
.
|

\
|
=
+ =

r
r
v
v
v v v

1
2 2
tan
The r-component of v is merely the rate at which
the vector r stretches.
The -component of v is due to the rotation of r.
Acceleration
Differentiating the expression for v to obtain
the acceleration a.
But from the previous derivation
dt
e d
r e
dt
d
r e
dt
dr
dt
e d
r e
dt
r d
a
e r e r
dt
d
dt
r d
dt
v d
a
r
r
r

+ + + + =
|
.
|

\
|
+ = = =
2
2
r
r
e
dt
de
and e
dt
de
. , .

= =

Substituting the above and simplifying

Where

e r r e r r a
e r e r e r e r e r a
r
r r


|
.
|

\
|
+ +
|
|
.
|

\
|
=
|
.
|

\
|
+ + + + =


2
2
|
.
|

\
|
+ =
|
|
.
|

\
|
=

r r a
r r a
r
2
2
|
|
.
|

\
|
=
+ =

r
r
a
a
a a a

1
2 2
tan
For motion in a circular path
Velocity
Where, because r=constant
Acceleration
where,

e r e r v
r

+ = . .
0 =

e r v

= .
0 = =

r r

e r e r a
r
|
.
|

\
|
+
|
|
.
|

\
|
=

2
Kinematics of particles
Relative motion
Relative motion
Relative motion analysis : is the motion analysis of
a particle using moving reference system
coordinate in reference to fixed reference
system.
In this portion we will confine our
attention to:-
moving reference systems that translate but
do not rotate.
The relative motion analysis is limited to plane
motion.
Note: in this section we need
1. Inertial(fixed) frame of reference.
2. Translating(not rotating) frame of reference.
Consider two particles A and B that may have
separate curvilinear motion in a given plane or in
parallel planes.
X,Y : inertial frame of reference
X,y : translating coordinate system
Using vector addition:
position vector of particle B is
Where: r
A
, r
B
absolute position vectors
r
B/A
relative position vector of particle B (B
relative to A or B with respect to A)
A B A B
r r r
/
+ =
Differentiating the above position vector once we
obtain the velocities and twice to obtain
accelerations. Thus,
- Velocity - Acceleration
A B A B
A B A B
v v v
dt
r d
dt
r d
dt
r d
/
/
+ =
+ =
A B A B
A B A B
a a a
dt
v d
dt
v d
dt
v d
/
/
+ =
+ =
Note: In relative motion analysis, we employed
the following two methods,
1. Trigonometric(vector diagram) A sketch of
the vector triangle is made to reveal the
trigonometry
2. Vector algebra using unit vector i and j,
express each of the vectors in vector form.
Example 1
A 350m long train travelling at a constant speed of 40m/s crosses
over a road as shown below. If an automobile A is traveling at
45m/s and is 400m from the crossing at the instant the front of the
train reaches the crossing, determine
a) The relative velocity of the train with respect to the automobile,
and
b) The distance from the automobile to the end of the last car of the
train at the instant.
Example 2
For the instant represented, car A has a speed of
100km/h, which is increasing at the rate of 8km/h
each second. Simultaneously, car B also has a speed of
100km/h as it rounds the turn and is slowing down at
the rate of 8km/h each second. Determine the
acceleration that car B appear to have an observer in
car A.
Example 3
For the instant represented, car A has an acceleration in
the direction of its motion and car B has a speed of
72km/h which is increasing. If the acceleration of B as
observed from A is zero for this instant,
Determine the acceleration of A and the rate at which the
speed of B is changing.
Example 4
Airplane A is flying horizontally with a constant speed
of 200km/h and is towing the glider B, which is
gaining altitude. If the tow cable has a length r=60m
and is increasing at the constant rate of 5 degrees
per second, determine the velocity and acceleration
of the glider for the instant when =15
Constrained motion of connected
particles
Constrained motion(dependent motion)
Sometimes the position of a particle will depend
upon the position of another or of several particles.
If the particles are connected together by an
inextensible ropes, the resulting motion is called
constrained motion
Considering the figure, cable AB is subdivided into three segments:
the length in contact with the
pulley, CD
the length CA
the length DB
It is assumed that, no matter how A and B move, the length in
contact with the pulley is constant.
We could write:
constant = = + +
AB B CD A
l s l s
Differentiating with respect to time,
Differentiating the velocity equation
0 v v
0
B A
= +
= +
dt
ds
dt
ds
B A
0 a a
B A
= +
Important points in this technique:
Each datum must be defined from a fixed position.
In many problems, there may be multiple lengths like l
CD
that dont
change as the system moves. Instead of giving each of these
lengths a separate label, we may just incorporate them into an
effective length:
where its understood that
l = cable length less the length in contact with the pulley = l
AB
l
CD
.
constant = = + l s s
B A
constant 2 = = + + l s h s
B A
considering the fig, we could write:
where l is the length of the cable less
the red segments that remain
unchanged in length as A and B move.
Differentiating,
0 2
0 2
= +
= +
B A
B A
a a
v v
constant ) ( 2 = = + + l s h h s
B A
we could also write the length of
the cable by taking another datum:
Differentiating,
0 2
0 2
= +
= +
B A
B A
a a
v v
Consider the fig.,
Since L, r
2
, r
1
and b is
constant, the first and
second time derivatives
are:-
b r y
r
x L + + + + =
1
2
2
2

y x
y x


2 0
2 0
+ =
+ =
Consider the
following figure
. ) (
. 2
const y y y y L
const y y L
D C C B B
D A A
+ + + =
+ + =
NB. Clearly, it is impossible for the
signs of all three terms to be positive
simultaneously.
Example 1
Cylinder B has a downward velocity of 0.6m/s and an
upward acceleration of 0.15m/s
2
.
Calculate the velocity and acceleration of block A.

= x v
A
Example 2
Collars A and B slides along the fixed rods are
connected by a cord length L. If collar A has a
velocity to the right, express the velocity
of B in terms of x, v
A
, and s.

= s v
B
Part III
Kinetics of particles
Kinetics of particles
It is the study of the relations existing between
the forces acting on body, the mass of the body,
and the motion of the body.
It is the study of the relation between
unbalanced forces and the resulting motion.
Newton s first law and third law are sufficient
for studying bodies at rest (statics) or bodies in
motion with no acceleration.
When a body accelerates ( change in velocity
magnitude or direction) Newton s second law is
required to relate the motion of the body to the
forces acting on it.
Kinetics problems
Force-mass-acceleration method
Work and energy principles
Impulse and momentum method
Force, mass and acceleration
Newton s Second Law: If the resultant force
acting on a particle is not zero the particle will
have an acceleration proportional to the
magnitude of resultant and in the direction of the
resultant.
The basic relation between force and
acceleration is found in Newton's second law of
motion and its verification is entirely
experimental.
Consider a particle subjected to constant forces
We conclude that the constant is a measure of
some property of the particle that does not
change.
const
a
F
a
F
a
F
= = = = ...
2
2
1
1
This property is the inertia of the particle
which is its resistance to rate of change of
velocity.
The mass m is used as a quantitative measure
of inertia, and therefore the experimental
relation becomes,
F=ma
The above relation provides a complete
formulation of Newton's second law; it expresses
not only that the magnitude F and a are
proportional but also that the vector F and a have
the same direction.
Types of dynamics problems
Acceleration is known from kinematics conditions
Determine the corresponding forces
Forces acting on the particle are specified
(Forces are constant or functions F( t, s, v, )
Determine the resulting motion
Equation of motion and solution of problems
When a particle of mass m acted upon by several
forces. The Newtons second law can be
expressed by the equation
To determine the acceleration we must use the
analysis used in kinematics, i.e
Rectilinear motion
Curvilinear motion

= ma F
Rectilinear Motion
If we choose the x-direction, as the direction
of the rectilinear motion of a particle of mass
m, the acceleration in the y and z direction
will be zero, i.e

=
=
=
0
0
z
y
x
x
F
F
ma F
Generally,
Where the acceleration and resultant force are
given by
Z
Z
y y
x
x
ma F
ma F
ma F
=
=
=

2 2 2
z y x
z y x
a a a a
k a j a i a a
+ + =
+ + =
( )
2 2
2
) ( ) (

+ + =
+ + =
z y x
z y x
F F F F
k F j F i F F
Curvilinear motion
In applying Newton's second law, we shall make
use of the three coordinate descriptions of
acceleration in curvilinear motion.
Rectangular coordinates
Where and

=
=
y y
x x
ma F
ma F

= x a
x

= y a
y
Normal and tangential coordinate
Where

=
=
t t
n n
ma F
ma F

= = = v a
v
a
t n
,
2 2

Polar coordinates
Where and

=
=

ma F
ma F
r r
2

= r r a
r

+ = r r a
n
2
Examples
Example 1
Block A has a mass of 30kg and block B has a mass of
15kg. The coefficient of friction between all plane
surfaces of contact are and .
Knowing that =30
0
and that the magnitude of the
force P applied to block A is 250N, determine
a) The acceleration of block A ,and
b) The tension in the cord
15 . 0 =
s

10 . 0 =
k

Example 2
A small vehicle enters the top A of the circular path
with a horizontal velocity v
o
and gathers speed as it
moves down the path.
Determine an expression for the angle to the
position where the vehicle leaves the path and
becomes a projectile. Evaluate your expression for
v
o
=0. Neglect friction and treat the vehicle as a
particle
Exercise(problem 3/69)
The slotted arm revolves in the horizontal plane about
the fixed vertical axis through point O. the 2kg slider C
is drawn toward O at the constant rate of 50mm/s by
pulling the cord S. at the instant for which r=225mm,
the arm has a counterclocke wise angular velocity
w=6rad/s and is slowing down at the rate of 2rad/s
2
.
For this instant, determine the tension T in the cord
and the magnitude N of the force exerted on the slider
by the sides of the smooth radial slot. Indicate which
side, A or B of the slot contacts the slider.
Exercise (problem 3/43)
The sliders A and B are connected by a light rigid
bar and move with negligible friction in the slots,
both of which lie in a horizontal plane. For the
positions shown, the velocity of A is 0.4m/s to
the right. Determine the acceleration of each
slider and the force in the bar at this instant.
Exercise (problem 3/36)
Determine the accelerations of bodies A and B
and the tension in the cable due to the application
of the 250N force. Neglect all friction and the
masses of the pulleys.