173 - pr 05 - physics of a massive vector boson: Add to QED a massive photon field B

of mass M, which
couples to electrons via,

3
; [massive-boson/massless-fermion coupling constant] H g B d x g

(1.1)

A massive photon in the initial or final state has three possible physical polarizations corresponding to the
three spacelike unit vectors in the bosons rest frame. These can be characterized invariantly in terms of the
bosons 4-momentumk

as the three vectors

( ) i

, satisfying,

( ) ( ) ( ) ( )
( ) ( ) ; 0;
i j ij j ij i
k e

= = = (1.2)

The four vectors
1
(
M
k

form a complete orthonormal basis. Because B

couples to the conserved current

,
the Ward identity implies that k

dotted into the amplitude for B-production gives zero thus we can replace:
( ) ( )* i j
i
g

. This gives a generalization to massive bosons of the Feynman trick for photon-
polarization-vectors and simplifies the calculation of B production cross sections. (Warning: This trick does not
work so simply for non-Abelian gauge fields). Lets do a few of these computations, using always the
approximation of ignoring the mass of the electron.


a) Compute the cross section for the process: e e B
+
. Diagram for this process and its time-reversed
counterpart (for consideration of decay, later) appears as,
(1.3)

Cross section necessitates a computation of amplitude, and we use QFT 02 106 [4.79], which reads,

3
3
2
1
2
(2 ) 4 (4)
( ) ( , { }
[4.79] (2 ) ( )
2 2
f
f
d p
A B f E
f
A B f
f
A B A B
p p p
d p p p
E E v v

= +

M
(1.4)

Corresponding amplitude is obviously
* *
2 1 2 1
( )[ ] ( ) ( ) v p g u p k gv u


= i i i M , where this time we have a
polarization-vector; its square summed over polarizations, using vv p = ,
*
g

= , 2

= 1, and
2 1 1 2
Tr[ ] p p p p

= 1 , then appears as,

2 1
2 1 2 1
2
2 * 2 2
1 1
2 2 1 1 2 1 4 4 4
spins
2 2 2 2
2 1 1 2 4 4
Tr[ ] Tr[ ]( ) Tr[ ]
Tr[ ( 2 )] ( 2) Tr[4 ] 2 Tr[ ] 2
p p
p p p p
g v v u u g p p g g
g g g g p p g p p

= = =
= = = =

1
M
(1.5)

Meanwhile: the cross section (1.4) is computed in the center of mass frame, which is characterized by,

2 2 2
1 1
1 2 2 2 2 2
; ; 2; ; ( ) ( ) ;
M M
f A B A B i f
E M E E M v v p p M = = = = = = = = p p 0 (1.6)

Thus, the cross section (1.4) is,

2
2
4 3 (4 3) 2 2
1
2 3
1 1
spins
2 2
1 1
(2 ) ( ) 2 ( ) ( )
2 2 2 2 2 2
i i i
g
d E M g M E M E M
M M M M M



= = = =

M (1.7)

Compute the lifetime of this B vector-particle assuming that it decays only to electrons. The lifetime is the
inverse of the decay rate. The decay rate is given by QFT 02 107 [4.86], appearing as,

3
2
4 (4)
3
3 3
2
4 (4) 1 2
1 2 3 3
spins
2 2
1 1
[4.86] ( { } (2 ) ( )
2 (2 ) 2
1
[ ] (2 ) ( )
2 (2 ) 2 2
f
A f B f
f A f
B
M M
d p
d M m p p p
m E
d p d p
T p E E
M

+
| |
=
|
|
\
1 1
=

M
(1.8)

Here, [ ] T M is the time reversed amplitude of (1.3), and it is computed using QFT 02 67 [3.133].

The sizes of the spin-spaces: Particle B is a spin-1 particle and the products are spin-1/2 particles. The vector-
particle B can have 0 0 0 1 = polarizations, and e+e- can have
1 1
2 2
(0 0) (0 0) ( ) ( ) 4 = =
polarizations, and the polarization degeneracy has the effect,

2
2 2
* 2 2 2
deg 1 2
spins spins spins deg
1 1 4
[ ] 4 4 2 ;
3 3 3
T g p p g M = = = =

M M M (1.9)

Putting (1.9) into (1.8) with
3 (3)
2 1 2
( )
B
d p = p p p 1 for decay in the CM-frame, we get a decay rate,

2 2 2
1
2 2 1 2 2 1 1 1 1 2
1 3 3 3 3 3 3
( ) 4 1 4 1 4
(2 ) ( 2 ) (2 )
2 (2 ) 3 2 (2 ) 3 12
lifetime
M d dp Mg
d g M M p g M T
M M

= = = =

p
(1.10)

Verify the relation discussed in Section 5.3, QFT 02 151 [5.58]. this relation specialized (well, not really)
to our case appears as,

2 2 2 2 2
3 ( ) ( )
[5.58] ( ) 4 ( ) ( ) 12 ( )
CM
B e e B e e
e e B E M e e B s M
M M

+ +
+ +

= = (1.11)

Computing
2 2
2
12 12
( ) ( )
M M
B e e s M


+
= and using
1
( ( )) ( )
i f
f x x x

, we get,

2 2 2 2
2 2 2
12 12 ( ) ( )
( ) ( )
12 2 0 2
i i
i
Mg E M E M g
E M g E M
M M E M

+ +
= = = =

(1.12)

(b) Compute the differential cross section in the center-of-mass system for the process: e e B
+
+ .

The differential cross section is given by,

1 2 1 2
2
2 2
2 2 2 2
helicities
1 1 1 1
1 1
[4.85] ;
64 cos 128 ( ) 128 ( )
CM
s s r r
CM
d d
d E d p k p k


= = =
+ +

M
M M (1.13)

By crossing-symmetry, you have contribution from the t and u Mandelstam-channels (c.f., QFT 02 -157). The
consequence of this: for any pair-annihilation process you have contributions from the diagrams given by QFT
02 168, as,
(1.14)

Correspondingly: for [ , ] 0

= ,
2
1
0 [photon-mass] k = = , the massive
2 2
2 B
k m = , and
2 2
1
p m = , the
Mandelstam variables
1 1
2p k t

= and
1 2
2p k u

= , and finally considering

2
1
, s p m >> (i.e., we neglect the
fermion masses) the amplitudes are,

1 1 1 2 * * * *
1 2 1 1 2 2 2 1 1 2 2 2
1 1 1 2
1 1 1 2 * * * *
2 1 1 2 2
2 2
2 2 2 2 1 1 2 2
1 1 1 2
1 2 2
( ) ( ) ( ) ( )
( ) ( )
; ;
2 0 2
(
B
p k m p k m
v g e u v e g u
p k p k
p k m p k m
gev u gev u
p k p k m
g
m m
m m m m
ev

+ +
= =

+ +
= =
+ + + +
+ =
i i i i M M
M M
1 1 2 1 * *
1 1 2
( ) 0 ( ) 0
)
k p k p
u
t u

+ +
+

(1.15)

On neglecting the fermion mass: We notice that
2
m cancels in the denominator of the two amplitudes, so
ignorance of the fermion-mass loses first-order physics,
1
( ) m O .

The amplitude in the differential cross section, then, is, seen in (1.4), which necessitates we compute,

2 2 2 2 2
* * *
1 2 1 2 1 2 1 2 1 2
helicities
( ) ( ) ; ; = + + = + + +

M M M M M M M M M MM M M (1.16)

Interlude of trace-taking: Preparing ourselves for an obnoxious interlude of working out these terms, we first
cite Casimirs trace-trick,

4
2
4
helicities
* 0 0
1 2 1 2 2
all spins
QFT02, [5.4] Tr[( ) ( ) ]Tr[( ) ( ) ];
QFT00, [7.125] [ ( ) ( )][ ( ) ( )] Tr ( ) ( ) ; ;
e e e e
a b a b b b a a
e
p m p m k m k m
q
u p u p u p u p p m p m



+ +
= + +
= + + (

M
(1.17)

Then, computing the amplitudes of (1.16) using (1.17) upon (1.15) and
( ) ( )* ( ) ( )*
spins
i j i j
i
g

=

,

1 1 2 1
1 1 1 1 1 2 1 1
2
2
2 2
* *
2 1 1 2 2 2 2 2
spins spins spins
1 1 2 1 1 1 2 1
1 2
( ) ( ) ( )
1 1 1
Tr[ ] Tr[ ( ) ]
4 4 4
1
Tr[( ( ) )( ( ) )]
4
Tr[
4
k p k p
t u
k p k k p k k p
t
v u
e g e g
k p k p k p k p
g g k k
t u t u
g g












= = = +

= + +
= +

M M M
1 2 1 2 2 1 1 1 1 2 2 1 1 2 1 2
2
2 2
( ) ( ) ( ) ( ) ( )
1 1 1
1 2 2 3
]
Tr[ ( ) ]
4
k k p k k p k k p k k p k k p k
ut
u
ut
t u
g g
T T T T




+

+
+ + + M
(1.18)

In which,

1 1 1 1 1 1 2 1 1 1 1 1 2
2 1 1 1 2 1 2 1 1 2 1 1 2
Tr Tr[ ( ) ( ) ] ( )( ) Tr[ ];
Tr Tr[ ( ) ( ) ] ( )( ) T
T k p k k p k k p k p k k
T k p k k p k k p k p k k

= =
= =
2 2 1 1 1 1 2
3 2 1 2 1 1 2
r[ ];
Tr ( )( ) Tr[ ];
( )( ) Tr[ ];
T k p k p k k
T k p k p k k

=
=
(1.19)

We already worked out what the trace of an 8-fold product of independent-gammas is (and we wish to not do it
again); please consult QFT 02 - 170 - pr 02 Bhabha scattering (1.16) to (1.19) and (1.26)
1
). The results are,

( ) ( )
2
2
32
1 1 1 2 1 2 1 1 2 1
( 2)
64
2 2 1 2 1 2 1 1 2 1
( 2)
Tr 32( )( ) Tr 32( )( );
(Tr Tr ) 64( ) ;
g g T k p k p ut g g T k p k p
g g T T k k k k k k k p s s t u

= = = =
+ = = + +
(1.20)

Putting (1.20) into (1.19), and subsequently into (1.18), we get an amplitude, in which we can use
2
( )
B
s t u M E

+ + = + , where we consider
B
E M

<< so
2
B
s t u M + + = , and
1 1 2 1
k p k p ut = , yielding,

2 2
2
2 2
1 1 2 1 2 2
spins
1 1 1 16 ( )
[( )32( )( ) ] 4 [2( ) ]
4 4
B
M s e g s s t u u t
k p k p e g
t u ut t u ut
+ +
= + + = + +

M (1.21)

Subsequently: use
2 2
2
( ) sin
B
t M s

= and
2 2 2
2 2
( ) cos cot
B
u M s t

= = , we get the cross section by putting
(1.21) into (1.13), and, non-dimensionalizing using
2
1 / 0
B
x M s = , we get,

2
2 2 2
/ 2 2 2
2 2 2 2 2 2
2
(1 / ) (1 )
2
2 2
1 (2cos 1) 4 1 cos 4
(1 / ) (1 )
[2( ) ]
cos 2 2 2sin cos 2 sin
B
B
M s
x
M s x
B B
M s g M s d e g u t g x
d s t u ut s s

+ + + +

= + + = = (1.22)
; (1.23)

Afterword: The good news: this calculation goes over almost unchanged to the real process:
0
e e Z
+
+ .
This allows one to measure the number of decays of the Z
0
into unobserved final states which is, in turn,
proportional to the number of neutrino species.

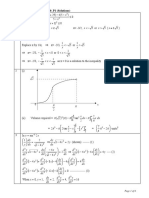
(c) Notice that the cross section of part b (1.22) diverges as 0, . Let us analyze the region near 0 = ,
where the dominant contribution comes from the t-channel diagram and corresponds intuitively to the emission
of a photon from the electron line before e+e- annihilation into a B-particle (see (1.14), righthand-diagram).

Let us rearrange the formula (1.22) in such a way as to support this interpretation. First: note that the
divergence as 0 is cut off by the electron mass. Let the electron momentum be
1
( , 0, 0, ) k E

= k and let the

photon momentum be
1
( , sin , 0, cos ) p xE xE xE

= with
2 2
e
E m = k . Under these conditions:
conservation says
2
((1 ) , sin , 0, cos ) p x E xE xE

= we have, and the Mandelstam variables appear as,

1
Please note that square brackets indicate Equation-numbers in the text, vs. the parentheses I use here which indicate equation
numbers in my homework. In short: look at Problem 5.2 worked in this assignment-submission.
-3 -2 -1 1 2 3
q
10
20
30
40
50
D_XS *sg
2
x=0.999
x=0.9
x=0.3
x=0.01
-3 -2 -1 1 2 3
q
-5
5
10
log @D_XS *sg
2
D
x=0.999
x=0.9
x=0.3
x=0.01

( )
( ) ( )
2
2 2 2 2
1 2 1 2 1 1
2 2
2
1 2
( ) ( ) 4 ; ( ) (1 ), sin , 0, cos ;
( ) (1 1 ) , 0 sin , 0, cos , sin , 0, cos ;
CM CM CM CM
s k k p p E t k p E x xE xE
u k p x E xE xE xE xE xE


= + = + = = =
= = = +
k
k k
(1.24)

Show that the denominator of the photon (book typo) propagator then never becomes smaller than
2
( / )
e
m s O
for all x. Correspondingly: the photon-propagator from QFT 00 244-246, in which ( / ) m s = O is the
tensor-element
2
/ ( )
t
G G g q g t

= = = i i , in which t is given by (1.24) and so we have,

2
2
2
2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2
1
4
2 2 2 2 2 2 2 2 2
1 1 1
4 4 4
4
(1 ) ( cos ) ( sin ) (1 ) ( ) ( )
2 2
/ 2 ( ) ( ) 1 2 ( ) (1 ) 2 1 2 (1 ) /
m
s
m E E E
m m m
E
t E x xE xE E x xE x E
E E x xE E m x E E m xE x m
t m x x x x x x m s

= = +
+ + +
= + = + > = =
k k O
(1.25)

Now: integrate (1.22) over forward-angles, cutting off the -integral at
2 2
~ /
e
m s , keeping only the leading
logarithmic term proportional to
2
log( / )
e
m s . Effecting this cut-off-integration upon (1.22) for cos = and
the
2
0
/ s m = , we get,

2
0 0
0
0
0 0
2
2 2 2
1 1
(1 ) 1
1 2 2
0 1 1
2 2 2 2
0 0
0 0 2 2
0 0
1 4
(1 ) (1 ) 1 1
sin ( ln )
cos 2 1 2 ( 1) 1
2 2 (1 ) 1 (1 ) 1
( 2ln (2 2 )) [ ln (1 )]
2 ( 1) ( 1)
x
x
d d g x g x x
d d d
d d s s x
g x x g x x g
s x s x

+ +
+
+
+ +
+ +
+ +
= = = =

+ +
= = =


2 2
0
0
0
1
ln ( )
1 2
x
s x

+
+

O
(1.26)

Show that in this approximation the cross section for forward photon emission can be written as,

2
2
(1 ) 0
1 (1 )
( ) ( ) ( ) lim ( ) ; ( ) log ;
2 CM
E x s x
e
x s
e e B f x e e B dx f x dx f x
x m

+ +
=
+
+ = =

(1.27)

where the annihilation cross section is evaluated for the collision of a positron of energy E and an electron of
energy (1 ) x E and the function ( ) f x being the Weiszacker-Williams distribution function, as given. Given the
four-momenta introduced in (1.24) and before, we have that ( ) e e B
+
is just the x = 0 case of the full cross
section ( ) e e B
+
+ . Computing the antiderivative of the RHS of (1.27) as instructed by the integral, and
putting (1.26) for x = 0 into (1.27) we get,

2 2 2 2 2 2
0 0
0 0
0 0
0 0
???
2 2 2 2
0
?
0
0
0 0
1 (1 ) 1 1 (1 )
lim ln ln ln ln lim
2 1 2 2 2
1
ln ln ln ln ( )
2 1
...
2
x x
x g x g x
dx dx
x s x s x
g g x
x e e B
s s x







+
+ + +
= =

+
= = = = +


(1.28)

Afterword: This function arises universally in processes in which a photon is emitted collinearly from an
electron line, independent of the subsequent dynamics. We will meet it again in another context in Problem 6.2.