Drill

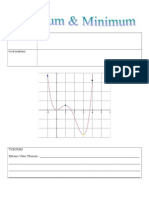
Look at the following graph. Notice that it is:

1. continuous on [-2, 2]
2. differentiable on (-2, 2)
3. and f(2) = f(-2)

Find the value of c, for which f (c) = 0

1

1. Draw two more graphs that have the same three properties as above, including at least one place where
f (c) = 0, but which look different.

2. Try to draw a graph that has the same three properties as above, but does NOT have a value c where f (c) =
0
3

Notes 4.2

First we have to talk another theorem

ROLLES THEOREM
_________________________ has three stipulations:
1. f is ______________________________________________________________________
2. f is ______________________________________________________________________
3. _________________________________________________________________________
If f satisfies the above three properties, then there is a number c in (a, b) such that
____________________________________________________________________________

MEAN VALUE THEOREM:

_________________________ has two stipulations:
1. f is _____________________________________________________________________________
2. f is _____________________________________________________________________________
If f satisfies the above three properties, then there is a number c in (a, b) such that
___________________________________________________________________________________

GRAPHICAL EXPLANATION:

EX 1: Verify that the function below satisfies the MVT, then find all numbers c that satisfy the conclusion of
the MVT: f(x) = x3 on [-2, 2]