Lecture XXI 61

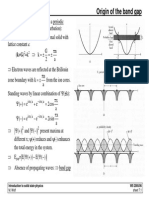
Lecture XXI: Cooper instability

In the nal section of the course, we will explore a pairing instability of the electron gas
which leads to condensate formation and the phenomenon of superconductivity.
History:
1911 discovery of superconductivity (Onnes)
1951 isotope eect clue to (conventional) mechanism
1956 Development of (correct) phenomenology (Ginzburg-Landau)
1957 BCS theory of conventional superconductivity (Bardeen-Cooper-Schrieer)
1976 Discovery of unconventional superconductivity in heavy fermions (Steglich)
1986 Discovery of high temperature superconductivity in cuprates (Bednorz-M uller)
???? awaiting theory?
(Conventional) mechanism: exchange of phonons can induce (space-nonlocal)
attractive pairwise interaction between electrons

=

H
0
[M[
2

kk

2
q
(
k

kq
)
2
c

kq
c

+q

c
k

c
k
Physically electrons can lower their energy by sharing lattice polarisation of another
By exploiting interaction, electron pairs can condense into macroscopic phase
coherent state with energy gap to quasi-particle excitations
To understand why, let us consider the argument marshalled by Cooper which lead to
the development of a consistent many-body theory.
Cooper instability
Consider two electrons propagating above a lled Fermi sea:
Is a weak pairwise interaction V (r
1
r
2
) sucient to create a bound state?
Consider variational state
(r
1
, r
2
) =
spin singlet
..
1

2
([
1
) [
2
) [
2
) [
1
))
spatial symm. g
k
= g
k
..

|k|k
F
g
k
e
ik(r
1
r
2
)
Applied to Schrodinger equation:

H = E

k
g
k
[2
k
+ V (r
1
r
2
)] e
ik(r
1
r
2
)
= E

k
g
k
e
ik(r
1
r
2
)
Lecture Notes October 2005
Lecture XXI 62
Fourier transforming equation: L
d
_
d(r
1
r
2
)e
ik

(r
1
r
2
)

V
kk
g
k
= (E 2
k
)g
k
, V
kk
=
1
L
d
_
dr V (r)e
i(kk

)r
If we assume V
kk
=
_

V
L
d
[
k

F
[, [
k

F
[ <
D
0 otherwise

V
L
d

g
k
= (E 2
k
)g
k

V
L
d

k
1
E 2
k

g
k
=

k
g
k

V
L
d

k
1
E 2
k
= 1
Using
1
L
d

k
=
_
d
d
k
(2)
d
=
_
() d (
F
)
_
d, where () =
1
[
k

k
[
is DoS
V
L
d

k
1
2
k
E
(
F
)V
_

F
+
D

F
d
2 E
=
(
F
)V
2
ln
_
2
F
+ 2
D
E
2
F
E
_
= 1
In limit of weak coupling, i.e. (
F
)V 1
E 2
F
2
D
e

2
(
F
)V
i.e. pair forms a bound state (no matter how small interaction!)
energy of bound state is non-perturbative in (
F
)V
Radius of pair wavefunction: g(r) =

k
g
k
e
ikr
, g
k
=
1
2
k
E
const.,
k
=

k
k

r
2
) =
_
d
d
r r
2
[g(r)[
2
_
d
d
r[g(r)[
2
=

k
[
k
g
k
[
2

k
[g
k
[
2

v
2
F
_

F
+
D

F
4d
(2E)
4
_

F
+
D

F
d
(2E)
2
=
4
3
v
2
F
(2
F
E)
2
if binding energy 2
F
E k
B
T
c
, T
c
10K, v
F
10
8
cm/s,
0
= r
2
)
1/2
10
4

A,
i.e. other electrons must be important
BCS wavefunction
Two electrons in a paired state has wavefunction
(r
1
r
2
) = ([
1
) [
2
) [
1
) [
2
))g(r
1
r
2
)
with zero centre of mass momentum
Drawing analogy with Bose condensate, let us examine variational state
(r
1
r
2N
) = ^
N

n=1
(r
2n1
r
2n
)
Lecture Notes October 2005
Lecture XXI 63
Is state compatible with Pauli principle? Using g(r
1
r
2
) =

k
g
k
e
ik(r
1
r
2
)
or, in Fourier representation
_
d
d
r
1
L
d
e
ik
1
r
1
_
d
d
r
2
L
d
e
ik
2
r
2
g(r
1
r
2
) =

k
g
k

k
1
,k

k
2
,k
or in second quantised form,
FT
_
g(r
1
r
2
)c

(r
1
)c

(r
2
)[)
_
=

k
g
k
c

k
c

k
[)
Then, of the terms in the expansion of
[) =
N

n=1
_

kn
g
kn
c

kn
c

kn
_
[)
those with all k
n
s dierent survive
Generally, more convenient to work in grand canonical ensemble
where one allows for (small) uctuations in the total particle density
[) =

k
(u
k
+ v
k
c

k
c

k
)[)
cf. coherent state
..
exp
_

k
g
k
c

k
c

k
_
[)
i.e. statistical independence of pair occupation
In non-interacting electron gas v
k
=
_
1 [k[ < k
F
0 [k[ > k
F
In interacting system, to determine the variational parameters v
k
,
one can use a variational principle, i.e. to minimise
[

H
F

N[)
BCS Hamiltonian
However, since we are interested in both the ground state energy, and the spectrum of
quasi-particle excitations, we will follow a dierent route and explore a simplied model
Hamiltonian

H =

k
c

k
c
k
V

kk

c
k
c
k
Lecture Notes October 2005