Quantum Chemistry Quantum Chemistry

QuantumChemistry Quantum Chemistry
Introduction Introduction
Statistical Averaging
Electromagnetic Spectrum Electromagnetic Spectrum
Black body Radiation
NC State Universityy
Overview Overview
Quantum Mechanics
Failure of classical physics p y
Wave equation
Rotational, vibrational and translational motion
Electronic structure
Spectroscopy
Statistical Mechanics
Partition function
Average energy
Entropy
Macroscopic viewof equilibrium Macroscopic view of equilibrium
For a chemical reaction in which X is the
reactant and Y is the product
X Y X Y
with free energy change AG
o
the equilibrium with free energy change AG
o
, the equilibrium
constant is
K =e
AG
o
/RT
=
[Y]
[X]
Microscopic viewof equilibrium Microscopic view of equilibrium
For a system where there are two energy
states, which we can call X and Y
YY
X
AE
X
with energy difference AE, the ratio of
population is
N
population is
where N and N are the numbers of
e
AE/kT
=
N
Y
N
X
where N
Y
and N
X
are the numbers of
particles in each state.
Boltzmanns constant Boltzmanns constant
Note that we k instead of R in the exponent.
k
B
is called Boltzmanns constant and it is
related to R by:
R
k =
R
N
A
B
where N
A
is Avagadros number.
k
B
T has units of J oules and is a measure of
the thermal energy of a molecule
RT has units of J oules/mole and is a measure
of the thermal energy of a mole
Microscopic probability Microscopic probability
When we look at the world in terms of energy
levels we can see that the probability of
being in a given level depends on temperature.
We define the probability of being in level j
as
number of molecules in state j
or
P
l
=
number of molecules in state j
total number of molecules
j
P
l
=
N
j
N +N
j
N
X
+N
Y
i
j
j
Microscopic probability Microscopic probability
We can calculate the probability of levels A
and B
P =
N
X
=
1
=
1
P
X
=
N
X
+N
Y
=
1 +N
Y
/N
X
=
1 +e
AE/kT
N N /N
AE/kT
P
Y
=
N
Y
N
X
+N
Y
=
N
Y
/N
X
1 +N
Y
/N
X
=
e
AE/kT
1 +e
AE/kT
Of course, P
X
+ P
Y
= 1
Average energy for
a two level system
We defined the relative energy of the two We defined the relative energy of the two
states as AE = E
Y
E
X
.
We can (arbitrarily) set the energy of state We can (arbitrarily) set the energy of state
X to zero, E
X
= 0.
Then the energy of state Y is E =AE Then the energy of state Y is E
Y
= AE.
The average energy of the system is:
<E >= P
j
E
j
E
i =1
=P
X
E
X
+P
Y
E
Y
e
AE/kT
E
e
AE/kT
AE =
e
1 +e
AE/kT
E
Y
=
e
1 +e
AE/kT
AE
Extension to many levels y
If we have a system with an infinite number
f ll d l l of equally spaced energy levels we can
calculate the probability and energy in the
same way.
jAE/kT
AE
P
j
=
e
jAE/kT
1 +e
AE/kT
++e
2AE/kT
++e
3AE/kT
+...
<E >= PE
E
AE
<E >= P
j
E
j
E
i =1
=
e
AE/kT
AE +2e
2AE/kT
AE +2e
3AE/kT
AE +...
1
AE/kT 2AE/kT 3AE/kT
3
1 +e
AE/kT
++e
2AE/kT
++e
3AE/kT
+...
Partition function for
l dd f l l ladder of energy levels
The denominator gives the average number of levels g g
that are accessible at a given temperature.
We can simplify it as follows:
Q =1 +e
AE/kT
+e
2AE/kT
+e
3AE/kT
+...
Let x =e
AE/kT
, then Q =1 +x +x
2
+x
3
+... , Q
Q 1 =x +x
2
+x
3
+x
3
+...
and
xQ =x +x
2
+x
3
+x
3
+...
since Q 1 =xQ
Q =
1
1 x
=
1
1 e
AE/kT
Calculating the energy
It is not obvious how to obtain the energy for this
system. We can consider the general formula and y g
make the substitution | = 1/kT.
<E >= P
j
E
j
E
<E > P
j
E
j
E
i =1
=
e
|AE
AE +2e
2|AE
AE +2e
3|AE
AE +...
1 +e
|AE
++e
2|AE
++e
3|AE
+
3
1 +e ++e ++e +...
=
cQ/c|
Q
For the energy ladder we have
1 e
|AE
e
|AE
AE
AE
<E >=
1 e
|AE
2
=
AE
e
|AE
1
High temperature limit
As the temperature approaches infinity all of the
levels become equally populated. The average
energy can be calculated assuming | = 1/kT << 1.
<E >=
AE
|AE
=
AE
1 |AE 1
=
1
|
=kT
Thus, kT is a classical energy for an averaged
E
e
|AE
1
1 |AE+.... 1 |
kT
Thus, kT is a classical energy for an averaged
system at high temperature. In units of joules/mole
<E >=RT
The energy of a gas is related to its PV
m
product
(V i th l l ) th
<E >=RT
(V
m
is the molar volume) thus,
PV
m
=RT
The wavelength and the frequency
f l t ti di ti of electromagnetic radiation
The wavelength is the distance between the
peaks in a traveling wave.
I l i l h i li ht i th t t l In classical physics light is a wave that travels
with velocity c. The frequency is v = c/.
The wavenumber v =v /c The
~
~
The wavenumber v v /c. The
wavenumber has units of cm
-1
.
~
The electromagnetic spectrum
increasing
v decreasing
The wavelength and frequency are inversely related
g
The wavelength and frequency are inversely related.
Frequency and wavelength are
inversely related inversely related
decreasing
v increasing
From the
Brittanica Encyclopedia
The electric field vector
The electric field vector is most important for
spectroscopy. The oscillation of the electric vector
i t t ith th h l d t d interacts with the charge clouds on atoms and
molecules to give rise to an oscillating dipole.
It is this oscillating dipole that gives rise to It is this oscillating dipole that gives rise to
spectroscopic transitions.
Poynting vector
Electric vector
Two extreme view of an oscillating dipole
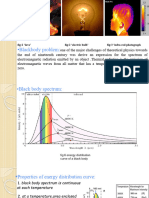
Black body Radiation Black body Radiation
An ideal emitter of radiation is called a black
body.
O f f Observation: that peak of the energy of
emission shifts to shorter wavelengths as the
temperature is increased temperature is increased.
Wien displacement law: Wien displacement law:
max
T = 2.88 x 10
6
nm-K.
Dilemma for Classical Physics Dilemma for Classical Physics
The maximum in energy for the black body
spectrumis not explained by classical physics spectrum is not explained by classical physics.
The cavity modes of the black body are
predicted to be predicted to be
=
8t k
B
T
4
Wh i th di t d it Thi f ti
4
Where is the radiant energy density. This function
increases without bound as 0. This law is known
as the Rayleigh-J eans law.
UV Catastrophe UV Catastrophe
=
8tk
B
T
The Planck Distribution Law The Planck Distribution Law

Planck assumed quantization of cavity
modes: E = nhv. (n=0,1,2..)
The constant h determines that only those
modes with an energy specified by the
i t i b it d precise amounts given can be excited.
The population of the levels will favor lower
( t b ) d energy (quantum number) modes over
higher energies.
Planck Assumption implies that average p p g
energy is temperature dependent
In classical physics the average energy in an
energy level is < E > = kT.
Quantized levels imply that the average energy in
each oscillator is < E > = hv/(e
hv/kT
- 1).
Si l it thi Since c = v we can also write this as
< E > = hc/(e
hc/kT
- 1).
To obtain the Planck formula simply replace kT To obtain the Planck formula simply replace kT
by the < E > = hc/ (e
hc/kT
- 1)
expression implied by quantization. expression implied by quantization.
Plancks Innovation
Classical radiation
All frequencies
Quantized radiation
Only frequencies nhv All frequencies
are possible
Only frequencies nhv
are allowed
Mathematical Form of
the Planck Law
The energy levels will be populated according to
a thermal weighting. The higher levels will be
l l t d th th l l l less populated than the lower levels.
In the Planck theory the energy density
becomes: becomes:
=
8t hc 1
=
5
e
hc / k
B
T
1
UV Catastrophe UV Catastrophe
=
8tk
B
T
Resolution of UV Catastrophe
8 h 1
=
8thc
5
1
e
hc / k
B
T
1
=
8tk
B
T
Planck Distribution Law Planck Distribution Law

Consistency with Experiment Consistency with Experiment
The temperature behavior of the Rayleigh- The temperature behavior of the Rayleigh
J eans law is recovered because
e
hc/kT
1 ~ hc/kT as T
The integral of the total energy is proportional
to T
4
which gives the Stefan-Boltzmann law,
W = oT
4
.
W is the flux or energy/area.
Th Wi di l t l i d f The Wien displacement law is recovered from
differentiation of . Setting d/d = 0 gives
the maximumin the distribution law. the maximum in the distribution law.
Wien displacement law
0
c
c 8t hc 1
0 =
c
c
=
c
c
8t hc
5
1
e
hc / k
B
T
1
Stefan-Boltzmann law
8 h 1
W = d
0
=
8t hc
5
1
e
hc / k
B
T
1
d
0
=oT
4
Consequences of Planck Law Consequences of Planck Law
Classical physics fails to describe black-
body radiation. A model that includes y
quantized modes of electromagnetic
radiation succeeds.
Plancks constant h = 6.626 x 10
-34
J s is
a fundamental constant the determines a fundamental constant the determines
the scale of energy quantization.
The Sun is a Black Body The Sun is a Black Body
The sun and stars are black bodies The sun and stars are black bodies
The peak of the emission spectrum
depends on temperature as indicated depends on temperature as indicated
by the Wien displacement law.
What is the radiant power of the sun?
Use the Stefan-Boltzman law
W= o T
4
(W is the flux or power per unit area) ( p p )
o = 5.6704 10
-8
kg s
-3
K
-4
(Watts/m
2
/K
4
)
Assuming that the temperature at the surface is 5500 K
and the diameter is 1 4 x 10
6
km and the diameter is 1.4 x 10 km.
The way that the Sun's diameter is measured is The way that the Sun s diameter is measured is
by taking angular diameter measurements and then
translating them to linear diameter measurements.
The angular diameter of the Sun can be measured using
a telescope during a total solar eclipse or by timing a telescope during a total solar eclipse or by timing
Mercury when it is in transit in front of the Sun. The first series
of measurements were taken in the early 1700's by Jean Picard in Paris, France.
What is the radiant power of the sun?
First calculate the area and then the flux (power).
The area is A = 4tR
2
A = 4(3.1416)(7 x 10
8
)
2
A=6 16 x 10
18
m
2
A = 6.16 x 10 m
The flux is
W T
4
W= o T
4
W = 5.6704 10
-8
(5500)
4
W = 5.19 x 10
7
Watts/m
2
The total power is
P =WA=(5 19 x 10
7
Watts/m
2
)(6 16 x 10
18
m
2
) P = WA= (5.19 x 10 Watts/m)(6.16 x 10 m )
P = 3.2 x 10
26
Watts
What is the radiant power at the surface
of the earth?
We use the distance from We use the distance from
the earth to the sun
to obtain the
fl t th th flux at the earth.
The earth is
R
e
= 1.5 x 10
8
km
from the sun.
The area
irradiated is
A 4 R
2
A
e
= 4tR
e
2
A
e
= 2.83 x 10
23
m
2
What is the radiant flux at the surface
The flux in space above the earth is called the insolation
of the earth?
The flux in space above the earth is called the insolation.
The insolation is the power coming from the sun divided
by the total area at the radius of the earth.
W P/A (3 2 10
26
W tt )/(2 83 10
23 2
) W
e
= P/A
e
= (3.2 x 10
26
Watts)/(2.83 x 10
23
m
2
)
W
e
= 1.13 x 10
3
Watts/m
2
This is very close to the measured
value for radiation in space
above the earth above the earth.
How much energy does the earth absorb?
The earth has a cross-sectional area of The earth has a cross sectional area of
A
c
= tR
earth
2
A
c
= (3.1416)(1.3 x 10
7
m)
2
A 5 3 10
14 2
A
c
= 5.3 x 10
14
m
2
P
abs
= W
e
A
c abs e c
P
abs
= (1.13 x 10
3
Watts/m
2
)(5.3 x 10
14
m
2
)
P
abs
= 6 x 10
17
Watts
What is the temperature at the surface
P
b
=P
it
=6 x 10
17
Watts
of the earth?
P
abs
P
emit
6 x 10 Watts
P
emit
= o T
earth
4
A
earth
[A
earth
= 4t R
earth
2
= 2.1 x 10
15
m
2
]
T
earth
= (P
emit
/o A
earth
)
1/4
T (6 10
17
/5 6704 10
8
/2 1 10
15
)
1/4
T
earth
= (6 x 10
17
/5.6704 10
-8
/2.1 x 10
15
)
1/4
T
earth
= 266 K
This is close, but it is a little frosty.
Why is this?
P.S. What is 266 K in
o
C?
What is 266 K in
o
F?
What is the temperature at the surface
P
b
=P
it
=6 x 10
17
Watts
of the earth?
P
abs
P
emit
6 x 10 Watts
P
emit
= o T
earth
4
A
earth
[A
earth
= 4t R
earth
2
= 2.1 x 10
15
m
2
]
T
earth
= (P
emit
/o A
earth
)
1/4
T (6 10
17
/5 6704 10
8
/2 1 10
15
)
1/4
T
earth
= (6 x 10
17
/5.6704 10
-8
/2.1 x 10
15
)
1/4
T
earth
= 266 K
This is close, but it is a little frosty.
Why is this?
We ignored the fact that
the earth has an atmosphere!
Th t h fl t b k The atmosphere reflects back
some of the radiated heat.
What is the role of the atmosphere?
1. Some molecules in the atmosphere absorb incident light.
Ozone absorbs UV light and prevents harmful radiation g p
from reaching the surface of the earth.
2 Molecules can also absorb emitted or radiated light 2. Molecules can also absorb emitted or radiated light.
What is the wavelength of such light? It can be obtained
from the Wien displacement law.
max
T = 2.88 x 10
6
nm-K
Thus for the sun withT =5500 K =523 nm Thus, for the sun with T = 5500 K,
max
= 523 nm
For the earth with T = 266 K,
max
= 10,800 nm = 10.8 m
f The suns emission is peaked in the visible region of the
Electromagnetic spectrum and the earth emits in the infrared.
Absorption by gases in the atmosphere
P
&
O

f
i
g

4
.
2
)
5500
o
K
266
o
K
s
s
i
o
n

b
y

(
s
o
u
r
c
e
:

P
a
n
d

e
m
i
s
b
s
o
r
p
t
i
o
n

s
e
s
l
e
c
t
i
v
e

a
b
p
h
e
r
i
c

g
a
3
.
5

S
e
l
a
t
m
o
s
p
Electronic Vibrational Rotational
The Wa e Particle D alit The Wave-Particle Duality
Th f t th t th D B li l th The fact that the DeBroglie wavelength
explains the quantization of the
h d t i h l hydrogen atom is a phenomenal
success.
Other wave-like behavior of particles
includes electron diffraction.
Particle-like behavior of waves is shown
in the photoelectric effect p
Photoelectric Effect
Electrons are ejected
froma metal surface by
e
-
from a metal surface by
absorption of a photon.
Depends on frequency,
hv
e
p q y
not on intensity.
Threshold frequency
corresponds to hv =u
Metal Surface
Kinetic
Energy
corresponds to hv
0
= u
u is the work function.
It is essentially equal to
hv
hv
u
u
gy
y q
the ionization potential
of the metal.
Insufficient energy
for photoejection
Photoejection occurs
Photoelectric Effect Photoelectric Effect
The kinetic energy of the ejected particle is given The kinetic energy of the ejected particle is given
by:
1/2 mv
2
= hv - u
The threshold energy is u, the work function.
This demonstrates the particle-like behavior of This demonstrates the particle like behavior of
photons.
A wave-like behavior would be indicated if the a e e be a o oud be dcated t e
intensity produced the effect.
Debroglie relation g
Light waves behave like particles in the
h t l t i ff t photoelectric effect.
Particles can also behave like waves. For
l l t diff t ( t f example, electrons can diffract (a property of
light waves).
Debroglie proposed a relationship between Debroglie proposed a relationship between
particle momentum and wavelength:
p =h/ p = h/
A light particle is called a photon. The
momentumis p =E/c Since c =v and E =hv momentum is p E/c. Since c v and E hv
this also gives p = h/.
Properties of exponentials Properties of exponentials
10
A
10
B
10
A+B
10
A
10
B
= 10
A+B
10
A
/10
B
=10
A-B
10
A
/10
B
= 10
A B
I f ti i l ith Inverse function is logarithm
l (10
A
) A log
10
(10
A
) = A
10
log
10
(B)
B 10
log
10
(B)
= B
Exponential to the base e Exponential to the base e
e
A
e
B
= e
A+B
e
A
/e
B
= e
A-B
Inverse function
is natural logarithm
ln(e
A
) = A
e
ln(B)
= B
Converting from
one base to another
10
A
= e
x
What is x?
A
ln(10
A
) = ln(e
x
) Take natural ln
of both sides
Aln(10) =x Solvefor x Aln(10) x Solve for x
x=23025A x = 2.3025A
Derivative: rate of change Derivative: rate of change
A c Ay cy
Ax cx
=
Slope Infinitesimal
Rate of change
Example function: parabola
Slope = - 80
x = - 40
Slope = - 40
x = - 20
Slope = 0
x = 0
Slope = 40
x = 20
Slope = 80
x = 40
What is the pattern? Slope = 2x
Plot the slope as the green points.
It is indeed a line with slope 2x.
Derivatives and Integrals
of the logarithm
Derivative dln(x)/dx = 1/x.
Integral definition of natural logarithm:
da
x
exp(x) is inverse of ln(x).
ln(x) =
da
a
1
exp(x) is inverse of ln(x).
The integral is the inverse of the derivative The integral is the inverse of the derivative.
Plot of the natural logarithm Plot of the natural logarithm
Slope of the tangent line at 1/4 Slope of the tangent line at 1/4
The derivative is the slope The derivative is the slope
x=1/4 , slope = 4
Slope of the tangent line at 1/2 Slope of the tangent line at 1/2
x=1/2 , slope = 2
Slope of the tangent line at 1 Slope of the tangent line at 1
x=1 , slope = 1
Slope of the tangent line at 2 Slope of the tangent line at 2
x=2 , slope = 1/2
Plot of the slopes of the tangents Plot of the slopes of the tangents
Plot of slope vs. x
Derivative dln(x)/dx =1/x Derivative dln(x)/dx = 1/x
f(x) = 1/x
g(x) = ln(x)
Integral of da/a:
the area under the curve
l (2)
da
2
ln(2) =
da
a
1
g(x) = ln(x)
f(a) = 1/a
Integral of da/a:
th ti f th the negative of the
area under the curve
ln(1/2) =
da
1/2
=
da
1
ln(1/2)
a
1
a
1/2
g(x) = ln(x)
f(a) = 1/a
Derivation of the Schrdinger Equation g q
The Schrdinger equation is a wave equation.
J ust as you might imagine the solution of such an equation J ust as you might imagine the solution of such an equation
in free space is a wave. Mathematically we can express a
wave as a sine or cosine function. These functions are
ll f ll d h oscillating functions. We will derive the wave equation in
free space starting with one of its solutions: sin(x).
Before we begin it is important to realize that bound states
may provide different solutions of the wave equation than
those we find for free space Bound states include those we find for free space. Bound states include
rotational and vibrational states as well as atomic wave
functions. These are important cases that will be treated
h f d t l d t di f th i i f once we have fundamental understanding of the origin of
the wave equation or Schrdinger equation.
The derivative
The derivative of a function is the instantaneous rate of change.
The derivative of a function is the slope The derivative of a function is the slope.
We can demonstrate the derivative graphically.
W id th f ti f( ) i ( ) h b l We consider the function f(x) = sin(x) shown below.
The derivative of sin(x) ( )
At sin(0) the slope is 1 as shown by the blue line.
At sin(t/4) the slope is 1/\2 as shown by the blue line.
At sin(t/2) the slope is 0 as shown by the blue line.
At sin(3t/4) the slope is -1/\2 as shown by the blue line.
Th l f ll li h f l d bl k The slopes of all lines thus far are plotted as black squares.
At sin(t) the slope is -1 as shown by the blue line.
We see from of the black squares (slopes) that the
d i i f i ( ) i ( ) derivative of sin(x) is cos(x).
d
sin(x) = cos(x)
d
dx
The derivative of cos(x) ( )
d
cos(x) =-sin(x)
d
dx
The second derivative of sin(x) ( )
d
d
sin(x) =-sin(x)
d
dx
d
dx
The second derivative of sin(x) ( )
d
2
sin(x) =-sin(x)
d
2
dx
2
Sin(x) is an eigenfunction ( ) g
If we define as an operator G then we have:
d
2
dx
2
-
sin(x) =sin(x)
d
2
-
dx
2
sin(x) sin(x)
dx
2
which can be written as:
Gsin(x) =sin(x)
This is a simple example of an operator equation that
is closely related to the Schrdinger equation. is closely related to the Schrdinger equation.
Sin(kx) is also an eigenfunction ( ) g
We can make the problem more general by including
a constant k This constant is called a wavevector a constant k. This constant is called a wavevector.
It determines the period of the sin function. Now we must
take the derivative of the sin function and also the
sin(kx) kcos(kx)
d
function kx inside the parentheses (chain rule).
sin(kx) =-kcos(kx)
dx
-
d
2
sin(kx) =k
2
sin(kx)
d
2
dx
2
-
Here we call the value k
2
the eigenvalue.
Sin(kx) is an eigenfunction ( ) g
of the Schrdinger equation
The example we are using here can easily be expressed
as the Schrodinger equation for wave in space. We only
have to add a constant. have to add a constant.
sin(kx) = sin(kx)
d
2
-
h
2 -
h
2
k
2 -
In this equation h is Plancks constant divided by 2t and
sin(kx) sin(kx)
dx
2
2m 2m
-
In this equation h is Plancks constant divided by 2t and
m is the mass of the particle that is traveling through space.
The eigenfunction is still sin(kx), but the eigenvalue in
this equation is actually the energy this equation is actually the energy.
The Schrdinger equation g q
Based on these considerations we can write a compact
formfor the Schrdinger equation form for the Schrdinger equation.
H+ =E+
d
2
d
2
-
h
2
2m
-
H =
Energy operator, Hamiltonian
dx
2
2m
h
2
k
2 -
E =
h
2
k
2
2m
Energy eigenvalue, Energy
+=sin(kx)
Wavefunction
The momentum
The momentum is related to the kinetic energy. Classically
The kinetic energy is:
E = mv
2
1
E = mv
2
The momentum is:
2
p = mv
So the classical relationship is: p
p
2
E =
2m 2m
If we compare this to the quantum mechanical energy:
h hk
E
h
2
k
2 -
we see that: p = hk
E =
2m
The general solution to the g
Schrdinger equation in free space
The preceding considerations are true in free space.
Since a cosine function has the same form as a sine
function, but is shifted in phase, the general solution function, but is shifted in phase, the general solution
is a linear combination of cosine and sine functions.
+ Asin(kx) +Bcos(kx)
Wavefunction
The coefficients A and B are arbitrary in free space.
+=Asin(kx) + Bcos(kx)
Wavefunction
However, if the wave equation is solved in the presence
of a potential then there will be boundary conditions. of a potential then there will be boundary conditions.

Quantum Chemistry Quantum Chemistry

Diunggah oleh

Informasi Dokumen

Judul Asli

Hak Cipta

Format Tersedia

Bagikan dokumen Ini

Bagikan atau Tanam Dokumen

Opsi Berbagi

Apakah menurut Anda dokumen ini bermanfaat?

Apakah konten ini tidak pantas?

Hak Cipta:

Format Tersedia

Quantum Chemistry Quantum Chemistry

Diunggah oleh

Hak Cipta:

Format Tersedia

QuantumChemistry Quantum Chemistry

The Planck Distribution Law The Planck Distribution Law

Planck Distribution Law Planck Distribution Law

Anda mungkin juga menyukai