Homework #10

Section 4.3: Problems #2(d, g, and h) and #5

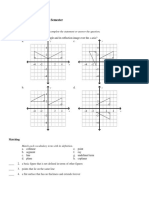
Problem #2: Which of the functions are one-to-one? Prove each of your answers.
(d) : f ,
3
) ( x x f =

Method (Direct Proof)
Statements Reasons
(1) ) ( ) ( v f u f = ; u and v are Assumed.
(2)
3 3
v u = From (1); using substitution into
3
) ( x x f = .
(3) v u = From (2); taking cube root of both sides.
f is one-to-one From (1) thru (3); by definition
1
.

1. Definition: A function B A f : is one-to-one iff whenever ) ( ) ( v f u f = , then v u = .
------------------------------------------------------------------------------------------------------------------------------------------
(g) : f , x x f sin ) ( =

Method (Counterexample)
Let: 0 = u so 0 ) 0 sin( ) 0 ( ) ( = = = f u f
t = v so 0 ) sin( ) ( ) ( = = = t t f v f
Therefore ) ( ) ( v f u f = , but v u = .
f is not one-to-one.
------------------------------------------------------------------------------------------------------------------------------------------
(h) : f , y x y x f = ) , (

Method (Counterexample)
Let: 1 , 0
1 1
= = v u so 1 1 0 ) 1 , 0 ( ) , (
1 1
= = = f v u f
0 , 1
2 2
= = v u so 1 0 1 ) 0 , 1 ( ) , (
2 2
= = = f v u f
Therefore ) , ( ) , (
2 2 1 1
v u f v u f = , but
1 1
v u = and
2 2
v u = .
f is not one-to-one.






Problem #5: Prove that if B A f
onto
: , and C B g
onto
: , then C A f g
onto
: (Theorem 4.3.1).

Method (Direct Proof)
Statements Reasons
(1) B A f
onto
: Given.
(2) C B g
onto
: Given.
(3) There exists some B b A a e e , , and C ce Assumed.
(4) c b g = ) ( From (2) and (3); since g is onto.
(5) b a f = ) ( From (1) and (3); since f is onto.
(6) )) ( ( ) )( ( a f g a f g = From (3) and definition of a composite.
(7) ) ( )) ( ( b g a f g = From (5) and (6); substitution.
(8) c b g = ) ( From (4) and (7); substitution.
(9) There exists some A ae that maps onto some From (6) thru (8).
arbitrary C ce
C A f g
onto
: From (1) thru (9).























Section 5.1: Problems #1, #3, and #12

Problem #1: Prove Theorem 5.1.1. That is, show that the relation ~ is reflexive, symmetric, and
transitive on the class of all sets.
Reflexive: Let S be any set; S S I
onto
S
1 1
:

, so S S ~ .
Symmetric: For sets S and T , assume T S ~ . Then there is a bijection T S f
onto
1 1
:

. Then S T f
onto
1 1
1
:

,
so S T ~ .
Transitive: Let V T S , , be sets such that T S ~ and V T ~ . Then there are bijections T S f
onto
1 1
:

and
V T g
onto
1 1
:

, so . :
1 1
V S f g
onto

Therefore V S ~ .
------------------------------------------------------------------------------------------------------------------------------------------
Problem #3: Complete the proof that any two open intervals ) , ( b a and ) , ( d c are equivalent by showing
that c a x
a b
c d
x f +
|
.
|

\
|

= ) ( ) ( maps one-to-one and onto ) , ( d c .

One-To-One
Assume ) , ( , b a y x e and ) ( ) ( y f x f = . Then ) ( ) ( a y
a b
c d
a x
a b
c d

|
.
|

\
|

=
|
.
|

\
|

, so y x = . Therefore
f is one-to-one.

Onto
Assume ) , ( , d c y x e . Then ) , ( ) ( b a a c y
c d
a b
e +
|
.
|

\
|

and y a c y
c d
a b
f =
|
.
|

\
|
+

) ( .
------------------------------------------------------------------------------------------------------------------------------------------
Problem #12: Prove that if Ais finite and B is infinite, then A B is infinite.

Method (Contradiction)
Statements Reasons
(1) Ais finite. Given.
(2) B is infinite. Given.
(3) A B is finite. Assumed; A B is NOT infinite.
(4) ) ( A B A B = is finite. From (1) and (3); Theorem 5.1.7
2

A B is infinite. From (1) thru (4); Contradiction in (2) and (4).

2. Theorem 5.1.7 (c): If
n
A A A ,..., ,
2 1
are finite sets, then
i
n
i
A
1 =
is finite.


Section 5.2: Problem #8

Problem #8: Give an example of denumerable sets Aand B , neither of which is a subset of the other,
such that
(a) B A is denumerable.
Let = A } 1 { + and = B } 2 { +
(b) B A is finite.
For an intersection to be finite, B A_ , A B _ , or B A~ ; therefore there are no sets that can
satisfy this with the condition that neither be a subset of the other.
(c) B A is denumerable.
Let = A and } 1 { = B
(d) B A is finite and nonempty.