Bohr Model
Diunggah oleh
thinkiitHak Cipta
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniBohr Model
Diunggah oleh
thinkiitChapter # 43 Bohr Model and Physics of the Atom
Page # 1
manishkumarphysics.in
SOLVED EXAMPLES
43.1 Calculate the energy of a He
+
ion in its first excited state.
Sol. The energy is E
n
=
2
2
n
RhcZ
=
2
2
n
Z ) eV 6 . 13 (
For a He
+
ion, Z = 2 and for the first excited state, n = 2 so that the energy of He ion in the first excited state
is 13.6 eV.
43.2 Calculate the wavelength of radiation emitted when He
+
makes a transition from the state n = 3 to the state
n = 2.
Sol. The wavelength is given by
|
.
|
\
|
=
2 2
2
m
1
n
1
RZ
1
=
R
9
5
9
1
4
1
R 4 = |
.
|
\
|
or, =
R 5
9
=
1 7
m 10 00737 . 1 5
9
= 164.0 nm.
43.3 The excitation energy of hydrogen-like ion in its first excited state in 40.8 eV. Find the energy needed to
remove the electron fromthe ion.
Sol. The excitation energy in the first excited state is
E = RhcZ
2
|
.
|
\
|
2 2
2
1
1
1
= (13.6 eV) Z
2
4
3
Equating this to 40.8 eV, we get Z = 2. So, the ion in question is He
+
. The energy of the ion in the ground
state is
E =
2
2
1
RhcZ
= 4 (13.6 eV)
= 54.4 eV.
Thus 54.4 eV is required to remove the electron from the ion.
QUESTIONS FOR SHORT ANSWER
1. Howmany wavelengths are emitted by atomic hydrogen in visible range (380 nm 780 nm)? In the range 50
nm to 100 nm ?
2. The first excited energy of a He
+
ion is the same as the ground state energy of hydrogen. Is it always true that
one of the energies of any hydrogen-like ion will be the same as the ground state energy of a hydrogen atom
?
3. Which wavelengths will be emitted by a sample of atomic hydrogen gas (in ground state) if electrons of
energy 12.2 eV collide with the atoms of the gas ?
4. When white radiation is passed through a sample of hydrogen gas at roomtemperature, absorption lines are
observed in Lyman series only. Explain.
5. Balmer series was observed and analysed before the other series. Can you suggest a reason for such an
order?
6. What will be the energy corresponding to the first excited state of a hydrogen atom if the potential energy of
the atom is taken to be 10 eV when the electron is widely separated from the proton? Can we still write
widely separated from the proton? Can we still write E
n
= E
1
/n
2
? r
n
= a
0
n
2
?
7. The difference in the frequencies of series limit of Lyman series and Balmer series is equal to the frequency
Chapter # 43 Bohr Model and Physics of the Atom
Page # 2
manishkumarphysics.in
of the first line of the Lyman series.. Explain.
8. The numerical value of ionization energy in eV equals the ionization potential in volts. Does the equality hold
if these quantities are measured in some other units?
9. We have stimulated emission and spotaneous emission. Do we also have stimulated absorption and spon-
taneous absorption?
10. An atom is in its excited state. Does the probability of its coming to ground state depend on whether the
radiation is already present or not? If yes, does it also depend on the wavelength of the radiation present?
Objective - I
1. The minimum orbital angular momentum of the electron in a hydrogen atom is -
ti:i- nii = :n+i- +i ---n +-ii +iii = n t -
(A) h (B) h/2 (C*) h/2t (D) h/
2. Three photons coming from excite3d atomic-hydrogen sample are picked up. Their energies are 12.1 V,
sample 10.2eV and 1.9eV. These photons must come from
(A) a single atom (B) two atoms (C) three atom
(D*) either two atoms or three atoms
--i l- nil+ti: i - + l-<zi = ~i- in -i- +i i-i +i -- l+i i-i t :-+i -i ( 12.1 eV, 10.2eV
~i 1.9eV t +i i- ~i t t . l-lz-- = -
(A) (+ ~+ n nii = (B) <i nii~i =
(C) -i- nii~i = (D*) i -i <i nii ~i = i -i- nii~i =
3. Suppose, the electron in a hydrogen atom makes transition from n = 3 to n = 2 in 10
8
s. The order of the
torque acting on the electron in this period, using the relation between troque and angular momentum as
discussed in the chapter on rotational mechanics is
ni-i l+ ti:i- nii n n = 3 = n = 2 -+ :n+i- +i =+ni 10
8
=+ n ti-i t := +in n :n+i-
nn t . n ~ii i +i +i l +i ni-. i i - i lzi+i + ~i n li - nii i ( +i ii = n + ~iii ti ni -
(A) 10
-34
N-m (B*) 10
-24
N-m (C) 10
-42
N-m (D) 10
-8
N-m
4. In which of the following transitions will the wavelength be minimum ?
(A) n = 5 to n = 4 (B) n = 4 to n = 3 (C) n = 3 to n = 2 (D*) n = 2 to n = 1
l--- =+nii n = l+=n -n< ---n tini -
(A) n = 5 = n = 4 (B) n = 4 = n = 3 (C) n = 3 = n = 2 (D*) n = 2 = n = 1
5. In which of the following systems will the radius of the first orbit (n=1) be minimum ?
(A) hydrogen atom (B) deuterium atom
(C) singly ionized helium (D*) doubly ionized lithium
l--- n = l+=n in +-ii (n=1) +i lzii - --n t -
(A) ti:i- nii (B) lln nii
(C) (+ii ~il-- tilnn (D*) l,~il-- lnlin
6. In which of the following systems will the wavelength corresponding to n=2 to n=1 be minimum ?
(A) hydrogen atom (B) deuterium atom
(C) singly ionized helium (D*) doubly ionized lithium
l--- n = l+=+ ln n=2 = n=1 + =n- -n< ---n t -
(A) ti:i- nii (B) lln nii
(C) (+ii ~il-- tilnn (D*) l,~il-- lnlin
Chapter # 43 Bohr Model and Physics of the Atom
Page # 3
manishkumarphysics.in
7. Which of the following curves may represent the speed of the electron in a hydrogen atomas a function of the
principal quantum number ?
l--- +i n = +i -=i ti: i - nii +i :n + i- +i -in +i n +in = i n + +n- n +- + =+-i
t -
(c*)
8. As one considers orbits with higher values of n in a hudrogen atom, the electric potential energy of the atom
(A) decreases (B*) increases (C) remains the same (D) does not increase
l< +i: ti: i- nii n n + --- ni-i + ln+-ii~i l-i +-i t. -i nii +i - l-il- -i -
(A) +n ti-i t (B*) c-i t (C) =ni- t-i t (D) c-i -ti t
9. The energy of an atom (or ion) in its ground state is - 54.4eV. It may be
(A) hydrogen (B) deuterium (C*) He (D) Li
l+=i nii (i ~i-) +i n n ~-ii n -i - 54.4eVt t ti =+-i t -
(A) ti:i- (B) lln (C*) He (D) Li
10. The radius of the shortest orbit in a one-electron system is 18 pm. It may be
(A) hydrogen (B) deuterium (C) He (D*) Li
(+n :n + i- l-+i n == zi i +-ii +i lzii 18 pm (l+i ni) t t ti =+-i t -
(A) ti:i- (B) lln (C) He (D*) Li
11. Ahydrogen atom in ground state absorbs 10.2eVof energy. The orbital angular momentumof the electron is
increased by
ti: i - nii n n ~-ii n 10.2eV-i ~zii li- +-i t :n + i- + +-ii +iii = n n lz ti -i t -
(A*) 1.05 x 10
-34
J-s (B) 2.11 x 10
-34
J-s (C) 3.16 x 10
-34
J-s (D) 4.22 x 10
-34
J-s
12. Which of the following parameters are the same for all hydrogen-like atoms and ions in their ground states ?
(A) radius of the orbitq (B) speed of the electron
(C) energy of the atom (D*) orbital angular momentum of the electron
ti: i - = =n-- nii~i ~i ~i-i +i nn ~-ii~i + ln l--- ilzii n = +i-=i (+ =ni- ti -i t -
(A) +-ii +i lzii (B) :n+i- +i -in
(C) nii +i -i (D*) :n +i- +i +-ii +i ii = n
13. In a laser tube, all the photons
(A) have same wavelength (B) have same energy
(C) move in same direction (D*) move with same speed
(+ n= -ni n. =i +ii-i -
(A) +i -n< =ni- ti-i t (B) +i -i =ni- ti-i t
(C) nl- +i l<zii =ni- ti -i t (D*) -in (+ =ni- ti -i t
Objective - II
1. In a laboratory experiment on emission from atomic hydrogen in a discharge tube, only a small number of
lines are abserved whereas a large number of lines are present in the hydrogen spectrum of a star. This is
because in a laboratory
(A) the amount of hydrogen taken in much smaller than that present in the star.
(B*) the temperature of hydrogen is much smaller than that of the star
(C) the pressure of hydrogen is much smaller than that of the star
(D) the gravitational pull is much smaller than that in the star.
Chapter # 43 Bohr Model and Physics of the Atom
Page # 4
manishkumarphysics.in
inziini n l=- -ln+i + in n nil+ ti:i- + -=- n . +n +z ti =i n ii l-i- ti-i
t . l+ -ii + ti: i - - + n n ii~i +i = i t - ~li+ ti -i t :=+i +ii t t l+ t - ~li+ ti -i t
:=+i +ii t t l+ i nziini n -
(A) ni ni ti: i - +i nizii. -ii +i -n-i n t - +n ti-i t
(B*) ti: i- +i -i. -ii +i -n-i n t- +n ti-i t
(C) ti:i- +i <i. -ii +i - n-i n t- +n ti -i t
(D) ni ~i+i i -ii +i - n-i n t - +n ti -i t
2. An electron with kinetic energy 5 eV is incident on a hydrogen atom in its ground state. The collision
(A*) must be elastic (B) may be partially elastic
(C) must be completely inelastic (D) may be completely inelastic
ti: i- nii +i n n ~-ii n := 5 eV nl- -i +i (+ :n + i- ~il-- ti -i t ++ -
(A*) l-lz-- = i-i ti ni (B) ~i lzi+ = i-i ti =+-i t
(C) i-i ~ i-i ti =+-i t (D) i-i ~ i-i ti =+-i t
3. Which of the following products in a hydrogen atom are independent of the principal quantum n ? The
symbols have their usual meanings
ti:i- nii + ln l--- ni-+ni n = +i-= n +in =i n l-i -ti +- t` =+-i +i =ini-
~i t -
(A*) un (B*) Er (C) En (D) ur
4. Let An be the area enclosed by the nth orbit in a hydrogen atom. The graph of
n
(A
n
/ A
1
) against
n
(n)
(A*) will pass through the origin (B*) will be a straight line with slope 4
(C) will be a monotonically increasing nonlinear curve (D) will be a circle
ni-i l+ ti:i- nii n n
th
+-ii +i -i zi+n
n
(A
n
/ A
1
) against
n
(n) -
(A*) nn l-< = nni (B*) (+ =n ii tini. l=+i cin 4
(C) (+n = c- ini ~li+ + tini (D) (+ -i ti ni
Sol. r
n
= n
2
r
1
ln
|
|
.
|
\
|
1
n
A
A
= ln
|
|
.
|
\
|
t
t
2
1
2
n
r
r
= ln n
4
= 4 ln (n)
4ln(n)
ln (A /A )
n 1
5. Ionization energy of a hydrogen-like ion B. Let r, u, E and L represent the radius of the orbit, speed of the
electron, energy of the atom and orbital angular momentum of the electron respectively. In ground state
ti:i - = ~i- A+i ~il-+i -i. (+ ~- ti: i- = ~i- B +i -i = ~li+ t ni-i l+ +-ii +i
lzii. :n + i- +i +-ii +i ii = n +nzi r, u, E ~i L,ii +- l+ i- t n n ~-ii n -
(A) r
A
> r
B
(B*) u
A
> u
B
(C) E
A
> E
B
(D) L
A
> L
B
6. When a photon stimulates the emission of another photon, the two photons have
(A*) same energy (B*) same direction (C*) same phase (D*) same wavelength
+ii- l+=i ~- +ii- + -=- +i -i-- +-i t. -i <i-i +ii- +i -
(A*) -i =ni- ti-i t (B*) l<zii =ni- ti-i t (C*) +ni =ni- ti-i t (D*) -n< =ni- ti-i t
WORKED OUT EXAMPLES
1. Find the radius of Li
++
ions in its ground state assuming Bohrs model to be valid.
it + nin +i = ni-- t( Li
++
~i- +i lzii +i ni-i +il( HCV_Ch-43_WOE_1
Sol. For hydrogen -like ions, the radius of the nth orbit is
a
n
=
Z
a n
0
2
For Li
++
, Z = 3 and in ground state n = 1. The radius is
a
1
=
3
pm 53
~ 18 pm.
2. A particular hydrogen-like ion emits radiation of frequency 2.467 10
15
Hz when it makes transition from
n = 2 to n = 1. What will be the frequency of the radiation emitted in a transition from n = 3 to n = 1?
Chapter # 43 Bohr Model and Physics of the Atom
Page # 5
manishkumarphysics.in
Sol. The frequency of radiation emitted is given by
v =
c
= K
|
|
.
|
\
|
2
2
2
1
n
1
n
1
Thus, 2.467 10
15
Hz = K
|
.
|
\
|
2 2
2
1
1
1
or, K =
3
4
2.467 10
15
Hz.
The frequency of the radiation emitted in the transition n = 3 to n = 1 is
v = K (
2 2
3
1
1
1
=
9
8
K =
9
8
3
4
2.467 10
15
Hz
= 2.92 10
15
Hz
3. Calculate the two highest wavelengths of the radiation emitted when hydrogen atoms make transitions from
higher states to n = 2 states.
Sol. The highest wavelength corresponds to the lowest energy of transition. This will be the case for the transition
n = 3 to n = 2. The second highest wavelength corresponds to the transition n = 4 to n = 2.
The energy of the state n is E
n
=
2
1
n
E
.
Thus, E
2
=
4
eV 6 . 13
= 3.4 eV
E
3
=
9
eV 6 . 13
= 1.5 eV
and E
4
=
16
eV 6 . 13
= 0.85 eV..
The highest wavelength is
1
=
E
hc
A
=
) eV 5 . 1 eV 4 . 3 (
nm eV 1242
= 654 nm.
The second highest wavelength is
2
=
) eV 85 . 0 eV 4 . 3 (
nm eV 1242
= 487 nm.
4. What is the wavelength of the radiation emitted when the electron in a hydrogen atoms jumps from n = to
n = 2?
Sol. The energy of n = 2 state is
E
2
=
4
eV 6 . 13
= 3.4 eV..
The energy of n = state is zero.
The wavelength emitted in the given transition is
l =
E
hc
A
=
eV 4 . 3
nm eV 1242
= 365 nm.
5. (a) Find the wavelength of the radiation required to excite the electron in Li
++
from the first to the third Bohr
orbit. (b) How many spectral linea are observed in the emission spectrum of the above excited system?
Sol. (a) The energy in the first orbit = E
1
= Z
2
E
0
where E
0
= 13.6 eV is the energy of a hydrogen atom in ground
state thus for Li
++
,
E
1
= 9E
0
= 9 ( 13.6 eV).
The energy in the third orbit is
Chapter # 43 Bohr Model and Physics of the Atom
Page # 6
manishkumarphysics.in
E
3
=
9
E
n
E
1
2
1
=
= 13.6 eV..
Thus, E
3
E
1
= 8 13.6 eV = 108.8 eV.
The wavelength of radiation required to excite Li
++
from the first orbit to the third orbit is given by
9
E
n
E
E
1
2
1
3
= =
= 13.6 eV..
Thus, E
3
E
1
= 8 13.6 eV = 108.8 eV.
The wavelength of radiation required to excite Li
++
from the first orbit to the third orbit is given by
1 3
E E
hc
=
or,
1 3
E E
hc
=
=
nm 4 . 11
eV 8 . 108
nm eV 1242
~
(b) The spectral lines emitted are due to the transitions n = 3 n = 2, n = 3 n = 1 and
n = 2 n = 1. Thus, there will be three spectral lines in the spectrum.
6. Find the wavelengths present in the radiation emitted when hydrogen atoms excited to n = 3 states return to
their ground states.
Sol. A hydrogen atom may return directly to the ground state or it may go to n = 2 and from there to the ground
state. Thus, wavelengths corresponding to n = 3 n = 1, n = 3 n = 2 are present in the radiation.
The energies in n = 1, 2 and 3 states are
E
1
= 13.6 eV
E
2
=
4
6 . 13
eV = 3.4 eV
and E
3
=
9
6 . 13
eV = 1.5 eV
The wavelength emitted in the transition n = 3 to the ground state is
=
E
hc
A
=
eV 5 . 1 eV 6 . 13
nm eV 1242
= 103 nm.
Similarly, the wavelength emitted in the transition n = 3 to n = 2 is 654 nm and that emitted in the transition
n = 2 to n = 1 is 122 nm. The wavelengths present in the radiation are, therefore, 103 nm, 122 nm and 654
nm.
7. Howmay different wavelengths may be observed in the spectrum from a hydrogen sample if the atoms are
excited to states with principal quantum number n ?
Sol. From the nth state, the atom may go to (n 1)th state, ...., 2nd state or 1st state. So there are
(n 1) possible transitions starting from the nth state. The atoms reaching (n 1)th state may make (n 2)
different transitions. Similarly for other lower states. The total number of possible transitions is
(n 1) + (n 2) + (n 3) +............2 + 1
=
2
) 1 n ( n
8. Monochromatic radiation of wavelength is incident on a hydrogen sample in ground state. Hydrogen atoms
absorb a fraction of light and subsequently emit radiation of six different wavelengths. Find the value
Sol. As the hydrogen atoms emit radiation of six different wavelengths, some of themmust have been excited to
n = 4. The energy in n = 4 state is
E
4
=
2
1
4
E
=
16
V e 6 . 13
= 0.85 eV
The energy needed to take a hydrogen atom from its ground state to n = 4 is
13.6 eV 0.85 eV = 12.75 eV
The photons of the incident radiation should have 12.75 eV of energy. So,
Chapter # 43 Bohr Model and Physics of the Atom
Page # 7
manishkumarphysics.in
hc
= 12.75 eV
or, =
eV 75 . 12
hc
=
eV 75 . 12
nm - eV 1242
= 97.5 nm.
9. The energy needed to detach the electron of a hydrogenlike ion in ground state is 4 rydberg. (a) What is the
wavelength of the radiation emitted when the electron jumps from the first excited state to the ground state
? (b) What is the radius of the first orbit for this atom ?
Sol. (a) In energy units, 1 rydberg = 13.6 eV. The energy needed to detach the electron is 4 13.6 eV. The energy
in the ground state is, therefore, E
1
= 4 13.6 eV. The energy of the first excited state (n = 2) is E
2
=
4
E
1
= 13.6 eV = 40.8 eV. The wavelength of the radiation emitted is
=
E
hc
A
(b) The energy of a hydrogen-like ion in ground state is E = Z
2
E
0
where Z = atomic number and E
0
= 13.6
eV. Thus, Z = 2. The radius of the first orbit is
Z
a
0
where a
0
= 53 pm. Thus,
r =
2
pm 53
= 26.5 pm
10. Ahydrogen sample is prepared in a particular excited stateA. Photons of energy 2.55 eV get absorbed into
the sample to take some of the electrons to a further excited state B. Find the quantum numbers of the
states A and B.
Sol. The allowed energies of hydrogen atoms are
E
1
= 13.6 eV
E
2
= 3.4 eV
E
3
= 1.5 eV
E
4
= 0.85 eV
E
5
= 0.54 eV
We see that a different of 2.55 eV can only be absorbed in transition n = 2 to n = 4. So the state A has
quantum number 2 and the state B has quantum number 4.
11. (a) Find the maximum wavelength
0
of light which can ionize a hydrogen atom in its ground state. (b) Light
of wavelength
0
is incident on a hydrogen atom which is in its first excited state. Find the kinetic energy of
the electron coming out.
Sol. (a) To ionize a hydrogen atom in ground state, a minimum of 13.6 eV energy should be given to it. Aphoton
of light should have this much of energy in order to ionize a hydrogen atom. Thus,
0
hc
= 13.6 eV
or, l
0
=
eV 6 . 13
nm - eV 1242
= 91.3 nm,
(b) The energy of the hydrogen atom in its first excited state is
4
eV 6 . 13
= 3.4 eV. Thus,
3.4 eV of energy is needed to take the electron out of the atom. The energy of a photon of the light of
wavelength
0
is 13.6 eV. Thus, the electron coming out will have a kinetic energy 13.6 eV 3.4 eV = 10.2
eV.
12. Derive an expression for the magnetic field at the site of the nucleus in a hydrogen atom due to the circular
motion of the electron. Assume that the atomis in its ground state and give the answer in terms of fundamen-
tal constants.
Sol. Wehave
r
mv
2
=
2
0
2
r 4
e
tc
Chapter # 43 Bohr Model and Physics of the Atom
Page # 8
manishkumarphysics.in
or v
2
r =
m 4
e
0
2
tc
............(i)
From Bohrs quantization rule, in ground rule, in ground state,
vr =
m 2
h
t
.........(ii)
From (i) and (ii),
v =
h 2
e
0
2
c
..........(iii)
and r =
2
2
0
me
h
t
c
...........(iv)
As the electron moves along a circle, it crosses any point on the circle
r 2
v
t
times per unit time. The charge
crossing per unit time, that is the current, is i =
r 2
eV
t
. The magnetic field at the centre due to this circular
current is
B =
2
0 0
v 4
ev
r 2
i
t
From(iii) and (iv),
B =
4 2
0
4 2 2
0
2
0
h
e m
h 2
e
4
e
c
t
c t
=
5 3
0
2 7
0
h 4
m e
c
t
13. A lithium atom has three electrons, Assume the following simple picture of the atom. Two electrons move
close to the nucleus making up a spherical cloud around it and the third moves outside this cloud in a circular
orbit. Bohrs model can be used for the motion of this third electron but n = 1 states ar not available to it.
Calculate the ionization energy of lithium in ground state using the above picture.
Sol. In this picture, the third electron moves in the field of a total charge + 3e 2e = + e. Thus, the energies are
the same as that of hydrogen atoms. The lowest energy is :
E
2
=
4
E
1
=
4
eV 6 . 13
= 3.4 eV
Thus, the ionization energy of the atom in this picture is 3.4 eV.
14. Aparticle known as -meason, has a charge equal to that of an electron and mass 208 times the mass of the
electron. It moves in a circular orbit around a nucleus of charge +3e. Take the mass of the nucleus to be
infinite. Assuming that the Bohrs model is applicable to this system, (a) derive an expression for the radius
of the nth Bohr orbit, (b) find the value of n for which the radius of the orbit is approximately the same as that
of the first Bohr orbit for a hydrogen atom and (c) find the wavelength of the radiation emitted when the
meson jumps from the third orbit to the first orbit.
Sol. (a) We have,
2
0
2 2
r 4
Ze
r
mv
tc
=
or,
m 4
Ze
r v
0
2
2
tc
==
...(i)
The quantization rule is vr =
m 2
nh
t
The radius is r =
r v
) vr (
2
2
=
2
0
Ze
m 4tc
Chapter # 43 Bohr Model and Physics of the Atom
Page # 9
manishkumarphysics.in
=
2
0
2 2
me Z
h n
t
c
....(ii)
For the given system, Z = 3 and m = 208 m
e
.
Thus
2
e
0
2 2
e m 624
h n
r
t
c
=
(b) From (ii), the radius of the first Bohr orbit for the hydrogen atom is
2
e
0
2
h
e m
h
r
t
c
=
For r
= r
h
,
2
e
0
2 2
e m 624
h n
t
c
=
2
e
0
2
e m
h
t
c
or, n
2
. = 624
or, n = 25
(c) From (i), the kinetic energy of the atom is
2
mv
2
=
r 8
Ze
0
2
tc
and the potential energy is
r 4
Ze
0
2
tc
The total energy is E
n
=
r 8
Ze
0
2
tc
Using (ii),
E
n
=
2 2 2
0
4 2
h n 8
me Z
tc
t
=
2 2 2
0
4
e
h n 8
m 208 9
c
=
2
n
1872
|
|
.
|
\
|
c
2 2
0
4
e
h 8
e m
But
|
|
.
|
\
|
c
2 2
0
4
e
h 8
e m
is the ground state energy of hydrogen atom and hence is equal to 13.6 eV..
From (iii), E
n
=
2
n
1872
13.6 eV =
2
n
eV 2 . 25459
Thus, E
1
= 25459.2 eV and E
3
=
9
E
1
= 2828.8 eV. The energy difference is E
3
E
1
= 22630.4eV..
The wavelength emitted is
=
E
hc
A
=
eV 4 . 22630
nm eV 1242
= 55 pm.
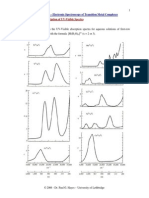
15. Find the wavelengths in a hydrogen spectrum between the range 500 nm to 700 nm.
Sol. The energy of a photon of wavelength 500 nmis
hc
=
nm 500
nm eV 1242
= 1.77 eV
The energy difference between the states involved in the transition should, therefore, be between 1.77 eVand
2.44 eV.
Chapter # 43 Bohr Model and Physics of the Atom
Page # 10
manishkumarphysics.in
n = 4, E = 0.85 eV
n = 3, E = 1.5 eV
n = 2, E = 3.4 eV
n = 1, E = 13.6 eV
Figure shows same of the energies of hydrogen states. It is clear that only those transitions which end at n
= 2 may emit photons of energy between 1.77 eV the proper range. The energy of the photon emitted in the
transition n = 3 to n = 2 is DE = (3.4 1.5) eV = 1.9 eV. The wavelength is
=
E
hc
A
=
eV 9 . 1
nm eV 1242
= 654 nm.
16. A beam of ultraviolet radiation having wavelength between 100 nm and 200 nm is incident on a sample of
atomic hydrogen gas. Assuming that the atoms are in ground state, which wavelength will have lowintensity
in the transmitted beam? If the energy of a photon is equal to the difference between the energies of an
excited being absorbed by an atom in the ground state.
Sol. The energy of a photon corresponding to = 100 nm is
nm 100
nm eV 1242
= 12.42 eV
and that corresponding to l = 200 nm is 6.21 eV.
The energy needed to take the atom from the ground state to the first excited state is
E
2
E
1
= 13.6 eV 3.4 eV = 10.2 eV,
to the second excited state is
E
3
E
1
= 13.6 eV 1.5 eV = 12.1 eV.
to the third excited state is
E
4
E
1
= 13.6 eV 0.85 eV = 12.75 eV etc.
Thus, 10.2 eV photons and 12.1 eV photons have large probability of being absorbed from the given range
6.21 eV to 12.42 eV. The corresponding wavelengths are
1
=
eV 1 . 10
nm eV 1242
= 122 nm.
and
1
=
eV 1 . 12
nm eV 1242
= 103 nm.
These wavelengths will have lowintensity in the transmitted beam.
17. Aneutron moving with speed v makes a head-on collision with a hydrogen atom in ground state kept at rest.
Find the minimum kinetic energy of the neutron for which inelastic (completely or partially) collision may take
place. The mass of neutron = mass of hydrogen = 1.67 10
27
kg.
Sol. Suppose the neutron and the hydrogen atom move at speed v
1
and v
2
after the collision. The collision will be
inelastic if a part of the kinetic energy is used to excite the atom. Suppose an energy AE is used in this way.
Using conservation of linear momentum and energy.
mv = mv
1
+ mv
2
....(i)
and
2
1
mv
2
=
2
1
mv
1
2
+
2
1
mv
2
2
+ AE ....(ii)
From(i), v
2
= v
1
2
+ v
2
2
+ 2v
1
v
2
,
From(ii), v
2
= v
1
2
+ v
2
2
+
m
E 2A
Thus, 2v
1
v
2
=
m
E 2A
Hence, (v
1
v
2
)
2
4v
1
v
2
= v
2
m
E 4A
As v
1
v
2
must be real,
v
2
m
E 4A
> 0
Chapter # 43 Bohr Model and Physics of the Atom
Page # 11
manishkumarphysics.in
or,
2
1
mv
2
> 2AE.
The minimum energy that can be absorbed by the hydrogen atom in ground state to go in an excited state is
10.2 eV. Thus, the minimum kinetic energy of the neutron needed for an inelastic collision is
eV 4 . 20 eV 2 . 10 2 mv
2
1
2
min
= =
18. Light corresponding to the transition n = 4 to n = 2 in hydrogen atoms falls on cesium metal (work function
= 1.9 eV). Find the maximum kinetic energy of the photoelectrons emitted.
Sol. The energy of the photons emitted in transition n = 4 to n = 2 is
hv = 13.6 eV (
2 2
4
1
2
1
= 2.55 eV..
The maximum kinetic energy of the photoelectrons is
= 2.55 eV 1.9 eV = 0.65 eV.
19. A small particle of mass m moves in such a way that the potential energy U =
2
1
m
2
e
2
r
2
where e is a
constant and r is the distance of the particle from the origin. Assuming Bohrs model of quantization of
angular momentum and circular orbits, show that radius of the nth allowed orbit is proportional to n .
Sol. The force at a distance r is
F =
dr
dU
= me
2
r.. ....(i)
Suppose the particle moves along a circle of radius r. The net force on it should be mv
2
/r along the radius.
Comparing with (i),
r
mv
2
= me
2
r
or, v = er ....(ii)
The quantization of angular momentumgives
mvr =
t 2
nh
or, v =
mr 2
nh
t
...(iii)
Thus, the radius of the nth orbit is proportional to
n
.
EXERCISE
1. The Bohr radius is given by a
o
=
2
2
o
me
h
t
c
Verify that the RHS has dimensions of length.
i t lzii a
o
=
2
2
o
me
h
t
c
,ii +- +i i-i t i - +il l+ <i i ~i +i ilzii +i lni( n-i: +i t
Ans :
2. Find the wavelength of the radiation emitted by hydrogen in the transitions (a) n = 3 to n = 2, (b)n = 5
to n = 4 and (c) n = 10 to n = 9.
ti:i- + ,ii l--- =+nii n -=l- ll+ii +i -n< ai- +il (a) n = 3 = n = 2,
(b) n = 5 = n = 4 ~i (c) n = 10 = n = 9
Ans: (a) 654 nm (b) 4050 nm (c) 38860
3. Calculate the smallest wavelength of radiation that may be emitted by (a) hydrogen, (b) He
+
and
Chapter # 43 Bohr Model and Physics of the Atom
Page # 12
manishkumarphysics.in
(c) Li
++
l--- + ,ii -=l- ti =+- in ll+ii +i ---n -< +i ni-i +il (a) ti:i- , (b) He
+
~i
(c) Li
++
Ans: (a) 91 nm (b) 23 nm (c) 10 nm
4. Evaluate Rydberg constant by putting the values of the fundamental constants in its expression.
ln l--i+ + + + nni- l--i+i +i ni- l--iil- ++. :=+i ni- ai- +il
Ans : 1.097 10 7 m
1
5 Find the binding energy of a hydrogen atom in the state n = 2.
n = 2 ~-ii n ti:i- nii +i i--i ai- +il
Ans : 3.4 eV
6. Find the radius and energy of a He
+
ion in the states (a) n = 1, (b) n = 4 and (c) n = 10.
He
+
~i- +i l--- ~-ii~i n lzii ~i -i ai- +il (a) n = 1, (b) n = 4 and (c) n = 10.
Ans : (a) 0.265 A, 54.4 eV (b) 4.24 A , 3.4 eV
7. A hydrogen atom emits ultraviolet radiation of wavelength 102.5 nm. What are the quantum numbers of
the states involved in the transition ?
(+ ti:i- nii 102.5 nm --ini -n< + in-i ll+i -=l- +-i t =+ni n iin n- in
~-ii~i +i +in = i( +i t `
Ans : 1 and 3
8. (a) Find the first excitation potential of He
+
ion (b) Find the ionization potential of Li
++
ion.
(a) He
+
~i- +i in --i - li ai- +il (b) Li
++
~i- +i ~i-- li ai- +il
Ans : (a) 40.8 V (b) 122.4 V
9. A group of hydrogen atoms are prepared in n = 4 states. List the wavelength that are emitted as the
atoms make transitions and return to n = 2 states .
ti: i - nii~i +i (+ =n t n = 4 ~-ii n -i l+i i-i t nii~i n = +ni = ~i n = 2 ~-ii~i n
ni- + +ii -=l- -n<i +i =-i -i:
Ans : 487 nm, 654 nm 1910 nm
10. A positive ion hydrogen just one electron ejects it if a photon of wavelength 228 of less is absorbed
by it identify the ion.
(+ i-i- + i= + n (+ :n + i - t . l< t 228 i :== +n - n< +i +i i - ~zii li- +-i t . -i :n + i -
-=l- + <-i t ~i- +i t-il-
Ans : He
+
11. Find the maximum coulomb force that can act on the electron due to the nucleus in a hydrogen atom.
ti:i- nii~i n -ili+ + +ii :n+ i- nn- ini ~li+-n +nini n ai- +il
Ans: 8.2 10
8
N
12. A hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with
excitation energy 10.2 eV (a) identify the quantum numbers n of the upper and the lower energy states
involved in the transition. (b) Find the wavelength of the emitted radiation.
0.85 eV i--i ~-ii +i ti: i - nii --i - -i 10.2 eV ini ~-ii n = +ni +-i t (a) := = +ni
n ziilnn - ini ~i -i- ini -i ~-ii~i +i +in = i( -i: (b) -=l - ll+i +i - n< ai-
+il
Ans: (a) 4, 2 (b) 487 nm
13. Whenever a photon is emitted by hydrogen in Balmer series it is followed by another photon in Lyman
series. What wavelength does this latter photon correspond to ?
ii ti: i - + ,ii in ii n +i i - -=l - l+i i-i t . ni:n- ii +i (+ ~- +i i- ii i-- ti -i t
i< in +ii- + =n- - n< +i t`
Ans: 122 nm
14. A hydrogen atom in stage n = 6 makes two successive transitions and reaches the ground state. In the
first transition a photon of 1.13 eV is emitted in the second transition (b) What is the value of n in the
intermediate state?
n = 6 ~-ii +i ti: i - nii <i +nin- = +ni ++ n n ~-ii n t --i t in = +ni n 1.13 eV +i +i i -
Chapter # 43 Bohr Model and Physics of the Atom
Page # 13
manishkumarphysics.in
-=l - ti -i t (a) l,-i = +ni n -=l - +i i - +i -i ai- +il (b) i- +i ~-ii + ln n +i ni- l+--i
t `
Ans: 121.eV , 3
15. What is the energy of a hydrogen atom in the first excited state if the potential energy is taken to be
zero in the ground state ?
l< n n ~-ii n l-il- -i zi - ni- ni i -i ti:i - nii +i in --il- ~-ii n -i l+--i ti ni`
Ans: 23.8 eV
15. What is the energy radiation of wavelengths 46.0 nm, 82.8 nm and 103.5 nm only. Assume that the atoms
have only two excited states and the difference between consecutive energy levels decreases as energy is
increased. Taking the energy of the highest energy state to be zero, find the energies of the ground state and
the first excited state.
l< nn ~-ii n l-il- -i zi - ni- ni i -i ti: i - nii +i in --i l- ~-ii n -i c- + =ii
<i +nin- -i --i +i ~ - +n ti -i t ----n -i ~-ii +i -i zi - ni-- t ( n n ~-ii ( in --i l-
~-ii +i -i ( ai- +il
Ans. 23.8 eV
16. A hot gas emits radiation of wavelengths 46.0 nm 82.8 nm and 103.5 nm only. Assume that the atoms
have only two excited states and the difference between consecutive energy levels decreases as energy
is increased. Taking the energy of the ground state and the first excited state.
(+ nn n= = +n 46.0 nm , 82.8 nm ~i 103.5 nm -n<i + ll+i -=l- ti- t ni- nil l+
nii ~i n + n <i ti --i l- ~-ii( t ~i -i c - + =ii <i +nin- -i . --i +i ~ - +n ti -i t ----n
-i ~-ii +i -i zi - ni-- t ( nn ~-ii ( in --i l- ~-ii +i -i( ai- +il
Ans: 27 eV , 12 eV
17. Agas of hydrogen like ions is prepared in a particular excited state Ait emits photons having wavelength
equal to the wavelength of the first line of the lyman series together with photons of five other wavelength
identify the gas and find the principal quantum number of the state A.
ti: i - = nii ~i +i (+ n = (+ llzi --i l- ~-ii An - i +i i-i t t ni:n- ii +i in ii
+ - - - n< + +ii-i + =ii i - ~- - n< i + +i i- -=l- +-i t n = +i t-il- ~i ~-ii A
+i n +in =i ai- +il
Ans: He
+
4,
18. Find the maximum angular speed of the electrons of a hydrogen atom in a stationary orbit.
ti:i- nii +i -iii +-ii n :n +i- +i ~li+-n +i ii -in ai- +il
Ans: 4.1 10
16
rad/s
19. A spectroscopic instrument can resolve two nearby wavelength and + A id /A is smaller than
8000 .This is used to study the spectral lines of the Balmer series of hydrogen Approximately how
many lines will be resolved by the instrument ?
(+ - + i-+il+ -+i <i =ni ini - n< i ~i + A +i li l<- + =+-i t . l< /A +i ni- 8000
= +n ti :=+i ti: i - +i in ii +i - + ni ii~i + ~- + ln +- l+i i-i t := -+i +
,ii =l--+- l+--i ii( lil<- +i i =+ni`
Ans: 38
20. Suppose in certain conditions only those transitions are allowed to hydrogen atoms in which the
principal quantum number n change by 2 (a) Find the smallest wavelength emitted by hydrogen (b) List
the wavelengths emitted by hydrogen in the visible range (380 nm to 780)
ni- nil l+. l+-ti llzi ll-il-i n ti: i - nii + + n ti = +ni = i t . l-n n +in = i
n n 2 +i l-- ti-i t (a) ti:i- ,ii --=l- ---n -n< ai- +il (b) ti:i- ,ii <z i=
(380 nm = 780nm) n -=l- -n<i +i =-i -i:
Ans: (a) 103 nm (b) 487 nm
21. According to Maxwells theory of electrodynamics an electrons going in a circle should emit radiation
of frequency equal to its frequency of revolution .What should be the wavelengths of the radiation
emdiation by a hydrogen atom in ground state if this rule is followed ?
- nl-+i (electrodynamics) + ln n += n + l=zi-- + ~- =i -ii+i i nn- +- ini :n + i -. i i -
+i ~i l-i + - - ~i l-i + ll+i -=l - + ni l< := l-n +i in- ti -i t . -i n n ~-ii + ti: i - nii
= -=l- ll+i +i -n< l+--i tini`
Chapter # 43 Bohr Model and Physics of the Atom
Page # 14
manishkumarphysics.in
Ans: 45.7nm
22. The average lometic energy of molecules in a gas at temperature T is KT .Find the temperature at
which the average kinetic energy of the molecules of hydrogen equals the binding energy of its atoms
will hydrogen remain in molecular form at this temperature ?Take K = 8.62 10
5
eV/K
l+=i n = + ~i ~i +i T -i ~i =- nl- -i 1.5 kT ti -i t t -i ai- +il l= ti: i - ~i ~i +i
~i =- nl- -i +i ni- :=+ nii ~i +i i- -i + i ti i +i := -i ti: i - ~il+ n
tni` Take K = 8.62 10
5
eV/K
Ans: 1.05 10
5
K
23. Find the temperature at which the average thermal kinetic energy is equal to the energy needed to take
a hydrogen atom from its ground state to n = 3 state. Hydrogen can now emit red light of wavelengths
653.1nm Because of Maxwellian distributions of speeds, a hydrogen sample emits red light at
temperature much lower than that obtained from this problem. Assume that hydrogen molecules
dissociate into atoms.
t -i ai- +il l= ~i =- -ni nl- -i +i ni-. ti: i - nii +i n n ~-ii = n = 3 ~-ii -+n
i- + ln ~iz+ -i + - - ti i ~ ti: i - 653.1 - -i ni - n< +i nin +izi -=l - + =+-i
t n += n + n l-i l-n + ~- =i. i-- l+ n -+- -i = t - +n -i ti ti: i - ~i . nii ~i n
li+- ti i- t
Ans: 9.4 10
4
K
24. Average lifetime of a hydrogen atom excited n = 2 state is 10
8
s. Find the number of revolutions made
by the electrons on the average before it jumps to ground state.
n = 2 ~-ii + --i - + ln ti: i - nii +i ~i =- ~i +in 10
8
= + t :n + i- ,ii n n ~-ii n + <-
= tn nni n -++i +i ~i =- =i ai- +il
Ans: 8.2 10
6
25. Calculate the magnetic dipole moment corresponding to the motion of the electrons in the ground state
of a hydrogen atom.
ti: i - nii +i nn~-ii n :n+i- +i nl- + =n- --+i l,i ~iii +i ni-i +il
Ans: 9.2 10
26. Show that the ratio of the magnetic dipole moment to the angular momentum ( = mnr) is universal
constant for hydrogen like atoms and ions. Find its value.
+- +il l+ ti: i - = nii ~i ( ~i-i + ln - -+i l,i ~ii i ~i +i ii = n ( = mnr) +i ~- i-
(+ =i lzi+ l--i+ t :=+i ni- ai- +il
Ans: kg / C 10 8 . 8
m 2
e
10
27. A beam of light having wavelengths distributed uniformly between 450 nm to 550 passes through a
sample of hydrogen gas. Which wavelength will have the least intensity in the transmitted beam ?
ti: i - n = = (+ +izi n -i t l=n 450 nm = 550nm -+ - n< (+ =ni- l-i t inln-
nl+= -n< +i -i-i ---n tini`
Ans: 487 nm
28. Radiation coming from transitions n = 2 to n = 1 of hydrogen atoms falls on helium ions in n = 1 and n
=2 states. What are the possible transitions of helium ions as they absorb energy from the radiation?
ti: i - nii n n = 2 = n = 1 = +ni +ii ~i- in ll+i n = 1 ~i n =2 ~-ii~i in tilnn ~i-i
~il-- ti - t l< tilnn ~i- :- ll+ii = -i ~zii li- +- t . -i :-n = i =+ni +i ti =+- t `
Ans: n = 2 to n = 3 and n = 2 to n = 4
29. Ahydrogen atom in ground state absorbs a photon of ultraviolet radiation of wavelength 50 nmAssuming
that the entire photon energy is taken up by the electron with what kinetic energy will the electrons be
ejected ?
(+ ti: i - nii n n ~-ii n 50 nm - n< + i n-i ll+i +i +i i - ~zii li- +-i t ni- nil l+
+ii- +i =-i -i :n+i- ,ii nti + ni i-i t. :n+i- l+--i nl- -i + =ii -=l- tini`
Ans : 11.24 eV
Chapter # 43 Bohr Model and Physics of the Atom
Page # 15
manishkumarphysics.in
30. A parallel beam of light of wavelength 100nm passes through a sample of atomic hydrogen gas in
ground state (a) Assume that when a photon supplies some of its energy to a hydrogen atom the rest
of the energy by the excited hydrogen atoms in the direction of the incident beam what wavelengths
may be observed in the transmitted beam ? (b) A radiation detector is placed neat the gas to detect
radiation coming perpendicular to the incident beam .Find the wavelengths of radiation that may be
detected by the detector.
100nm - n< +i +izi n n ~-ii +i nil+ ti: i - n = = n -i t (a) ni- nil l+ (+ +i i -
~-i + z -i ti: i- nii +i <i- +-i t. zii -i (+ ~- +ii- +i l<zii n ti nl- +-i t --i l-
nii ,ii ~il-- +i l<zii n -=l - +izi +i -n ni-- t ( inln- n +i -=i - n< i +i l-i- l+i
i ni` (b) ~il-- + n-- l<zii n ~i- in ll+ii +i = =l-- +- + ln (+ ll+i = =-+ +i n =
+ =ni ii i-i t ==-+ ,ii = =l-- ll+ii +i -n<i +i ni- ai- +il
Ans: (a) 100 nm , 560 nm 3880 (b) 103 nm, 121 nm 654 nm
31. A beam of monochromatic light of wavelength ejects photoelectrons from a cesium surface (| = 1.9
eV) These photoelectrons are made to collide with hydrogen atoms in ground state .Find the maximum
value of for which (a) hydrogen atoms may be ionised (b) hydrogen atoms may get excited from the
ground state to the first excited state and (c) the excited hydrogen atoms may emit visible light.
-n< +i (+ ii +izi =iln (| = 1.9 eV) +i =-t = +ii:n+i-i +i -=l- +-i t :-
+i i :n + i -i +i n n ~-ii in ti: i - nii ~i = ++ +ii i-i t +i t ~li+-n ni- ai- +il .
l=+ ln (a) ti:i - nii ~il-- ti =+-i t . (b) ti:i- nii nn ~-ii = in --il- ~-ii -+
--il- ti =+- t -ii (c) --il- ti:i- nii <z +izi -=l- + =+- t
Ans: (a) 80 nm( (b) 102 nm (c) 89 nm
32. Electrons are emitted from an electron gun at almost zero velocity and accelerated by an electric field
E through a distance of 1.0 m The electrons are now scattered by an atomic hydrogen sample in
ground state. What should be the minimum value of E so that red light of wavelength 656 .3 may be
emitted by the hydrogen ?
(+ :n+ i-n- = :n+ i- nnin zi - n = -=l - ti- t . ~i 1.0 m <i -+ l - -izi E = l- ti - t
~ iii :n + i - n n ~-ii + nil+ ti: i - l-<zi = +ili - ti - t E +i - --n ni- l+--i ti l+ ti: i -
= 656.3nm -n< +i nin +izi -=l- ti`
Ans: 12.1 V/m
33. A neutron having kinetic energy 12.5 eV collides with a hydrogen atom at rest Neglect the difference in
mass between the neutron and the hydrogen atom and assume that the neutron does not leaves its line
of motion Find the possible kinetic energies of the neutron after the event.
12.5 eV nl- -i +i - i -. lini-ii n l-i- (+ ti: i - + < ni- ~-- +i -n ni- nil ~i t ni-
nil l+ - i- :=+i nn- ii +i -ti zi -i t := i-i + z-i- -i- +i =i nl- -i( ai- +il
Ans: zero
34. A hydrogen atom moving at speed v colloids with another hydrogen atom kept at rest Find the minimum
value of v for which one of the atoms may get ionized the mass of a hydrogen atom = 1.67 10
27
kg.
v -in = nl-ziin (+ ti: i - nii lini-ii n l-i- (+ ~- ti: i - nii = +i-i t v +i t - --n
ni- ai- +il. l=+ ln ti:i- nii~i n = (+ ~il-- ti =+ ti:i- nii +i <ni- = 1.67
10
27
l+ni
Ans: 7.2 10
4
m/s
35. A neutron moving with a speed v strikes a hydrogen atom in ground state moving towards it with the
same speed .Find the minimum speed of the neutron for which inelastic (completely of partially) collision
may get ionized The mass of neutron = mass of hydrogen = 1.67 10
27
kg
v -in = nl-ziin (+ - i - :=+i ~i =ni- -in = nl-ziin n n ~-ii in ti: i - nii = +i-i t - i-
+i t - --n -in ai- +il . l=+ ln ~ i-i ( i -i i ~i lzi+) ++ ti =+ - i- +i t - --n -in
ai- +il . l=+ ln ~i-i (i-i i ~i lzi+) ++ ti =+ - i- +i < ni- = ti:i - +i < ni- =
1.67 10
27
l+ni
Ans: 3.13 10
4
m/s
Chapter # 43 Bohr Model and Physics of the Atom
Page # 16
manishkumarphysics.in
36. When a photons is emitted by a hydrogen atom, the photon carries a momentum with it(a) Calculate
the momentum carried by the photon when a hydrogen atom emits light of wavelength 656.3nm
(b) With what speed does the atom recoil during this transition ?Take the mass of the hydrogen
atom =1.67 10
27
kg (c) Find the kinetic energy of recoil of the atom
l+=i ti:i - nii = +i i- -=l - ti-i t . -i +ii- ~- =ii = n n i-i t (a) ti:i - nii
656.3 nm -n< +i +izi -=l- +-i t. -i +ii- ,ii n in=n +i ni-i +il (b) := =+ni n
nii n nii +i l--i -in +i ti ni` ni- nil l+ ti:i - nii +i < ni- 1.67 10
27
l+n i t (c)
l--il- nii +i nl- -i ai- +il
Ans : (a) 1.0 10 27 kg m/s (b) 0.6 m/s
37. When a photon is emitted from an atom the atom recoils. The kinetic energy of recoil and the energy
of the photon come from the difference in energies between the states involved in the energies between
the states involved transition suppose a hydrogen atom changes its state from n = 3 to n = 2 Calculate
the fractional change in the wavelength of light emitted, due to the recoil
l+=i nii = +ii- -=l- ti-i t. -i nii l--i l- ti-i t l--i + ln nl- -i ~i +i i- +i
-i = +ni n iin n - ini -i ~-ii~i +i -i ~i + ~-- = i-- ti -i t ni- nil l+ (+ ti: i - nii
:=+i ~-ii n = 3 = n = 2 -+ ll-- +-i t l--i + +ii -=l- +izi +i -n< n l+= nii+ =
l-- tini. ni-i +il
Ans: 10 9
38. The light emitted in the transition n = 3 to n = 2 in hydrogen is called H
o
light. Find the maximum work
function a metal can have so that Ho light can emit photoelectrons from it.
ti:i- nii n n = 3 = n = 2 =+ni = -=l- +izi H
o
+izi :== +ii:n+i- -=l- + =+
Ans: 1.9 eV
39. Light from Balmer series of hydrogen is able to eject photoelectrons from a metal .What can be the
maximum work function of the metal?
ti: i - +i in ii +i +izi l+=i ii- = +i i :n + i-i +i -=l - +- + ln =-in t ii- +i ~li+-n
+i+n- l+--i ti =+-i t`
Ans: 3.4 eV
40. Radiation from hydrogen discharge tube falls on a cesium plate. Find the maximum possible kinetic
energy of the photoelectrons .Work function of cesium is 1.9 eV.
ti: i - l= - -ln+i n -=l - ll+i =iln -n ~il-- ti - t +i i :n + i -i +i ~li+-n = i nl-
-i ai- +il =iln+i +i+n- 1.9 eV t
Ans: 11.7 eV
41. A filter transmits only the radiation of wavelength greater than 440 nm. Radiation from a hydrogen
discharge tube goes through such a filter and is incident on a metal of work function 2.0 eV Find the
stopping potential which can stop the photoelectrons.
l+=i l+- 440 nm = ~li+ -n< in ll+i inln- ti- t ti:i - l=- -ln+i = -=l - ll+i
( = ti l+- = n - + z-i- 2.0 eV +i +n- ini ii- +i =-t ~il-- ti - t l-i i+ li +i t ni-
ai- +il. i +ii:n+i-i +i i+ =+
Ans: 0.55
42. The earth revolves round the sun due to gravitational attraction Suppose that the sun and the earth are
point particles with their existing masses and that Bohar s quantization rule for angular momentum is
valid in the case of gravitation (a) Calculate the minimum radius the earth can have for its orbit (b) What
is the value of the principal quantum number v for the present radius ? Mass of the earth = 6.0 10
24
kg mass of the sun 2.0 10
30
kg earth sun distance = 1.5 10
11
m.
i n i+i i n + +ii = + -ii ~i l+ni +-i t ni- nil l+ i ( = :-+ < ni-i in l-< -
+i t -ii i t +i +i ii = n + +il+i +i l-n n i+i i + ln ii nin ti -i t (a) i +i +-ii +
ln = i - --n lzii +i ni-i +il (b) lzii + ~ii in ni- + ln n +in = i +i ni- l+--i ti ni`
i +i <ni- = 6.0 10
24
kg , = +i <ni- = 2.0 10
30
kg , i= +i <i = 1.5 10
11
m
Chapter # 43 Bohr Model and Physics of the Atom
Page # 17
manishkumarphysics.in
Ans: (a) 2.3 10
138
m (b) 2.5 10
74
43. Consider a neutron and an electrons bound to each other due to gravitational force .Assuming Bohar s
quantization rule for angular momentum to be valied in this case derive an expression for the energy of
the neutron - electron system.
ni- nil l+ (+ :n + i- ( (+ - i- n i+i i n + +ii - i t ( t ni- nil l+ := l-il- n
i t +i +i ii = n +il+i l-n nin ti -i t . - i-:n + i- l-+i + ln -i +i + l-nln- +il
Ans:
2 2
3
e
2
n
2
n h 2
m m G 2t
44. A uniform magnetic field B exists in a region An electron projected perpendicular to the field goes in a
circle Assuming Bohars quantization rule for angular momentum calculate (a) the smallest possible
radius of the electron (b) the radius of the n
th
orbit and (c) the minimum possible speed of the electron.
l+=i -ii- =n - -+i -i zi B lni- t -i zi + n-- -i l- (+ :n + i- -ii+i i nn- +-i t
i t +i +i ii = n +il+i l-n ni-- t (. ni-i +il : (a) :n + i - +i = i - --n lzii (b) ni +-ii +i
lzii. -ii (c) :n+ i- +i =i - --n -in
Ans: (a)
2
m 2
heB
) c (
eB 2
nh
) b (
eB 2
h
t
t t
45. Suppose in an imaginary world the angular momentum is quantized to be even integral multiples of h/
2p What is the longest possible wavelength emitted by hydrogen atoms in visible range in such a world
according to Bohrs model?
ni- nil l+ l+=i +i-l-+ < l-i n +i ii = n h/2t + =n n ii + ln +il|- t ( =i < l-i n i t l-
+ ~-=i ti:i- nii~i ,ii <z i= n -=l- -n< +i ~li+-n =i ni- l+--i ti =+-i t`
Ans: 487 nm
46. Consider an excited hydrogen atom in state n moving with a velocity v (v << c ).It emits a photons in the
direction of its motion and changes its state to a lower state mApply momentum and energy conservation
principles to calculate the frequency v of the emitted radiation compare this wite the frequency v
o
emitted if the atom were at rest.
v (v << c ) n = nl-ziin ( n ~-ii n --i l- ti: i - nii l-i +il t :=+i nl- +i l<zii n (+
+i i- -=l - +-i t . ~i :=+i ~-ii (+ l--- ~-ii m -+ ll- - + n -i t -=l - ll+i +i ~i l-i
+i ni-i +- + ln = n -ii -i + = -ii l-ni +i nin +il l< nii l-i ti -i -i -=l - ~i l-i v
o
+ =ii :=+i -n-i +il
Ans: v = v
o
|
.
|
\
|
+
c
v
1
Anda mungkin juga menyukai
- Magnetic FieldDokumen21 halamanMagnetic FieldthinkiitBelum ada peringkat
- X RaysDokumen9 halamanX RaysthinkiitBelum ada peringkat
- Atomic StructureDokumen22 halamanAtomic StructureYash AkhauriBelum ada peringkat
- Cairo University 3rd Year Chemistry ExamDokumen3 halamanCairo University 3rd Year Chemistry ExamKhaled AbeedBelum ada peringkat
- Kinetic Theory of GasesDokumen28 halamanKinetic Theory of Gasesthinkiit0% (1)
- Heat and TemperatureDokumen13 halamanHeat and TemperaturethinkiitBelum ada peringkat
- Electric Current in ConductorsDokumen31 halamanElectric Current in ConductorsthinkiitBelum ada peringkat
- Mordern Physics Type 1ggggggggggggggggggggggggggggDokumen20 halamanMordern Physics Type 1ggggggggggggggggggggggggggggvishal110085Belum ada peringkat
- CPP Atomic Structure MCQsDokumen3 halamanCPP Atomic Structure MCQsMohit Khanna100% (1)
- Light WavesDokumen15 halamanLight WavesthinkiitBelum ada peringkat
- Atomic Structure DPP #2 NSEJS23-24 @QOTDforOlympiadsDokumen1 halamanAtomic Structure DPP #2 NSEJS23-24 @QOTDforOlympiadsAnmol RajBelum ada peringkat
- Delhi Public School Bangalore North Academic Session 2022-23 Worksheet-Answer KeyDokumen6 halamanDelhi Public School Bangalore North Academic Session 2022-23 Worksheet-Answer KeyShashwatBelum ada peringkat
- Modern Physics Part 2Dokumen11 halamanModern Physics Part 2Shivam Jaggi100% (1)
- Bansal Classes Chemistry Study Material For IIT JEEDokumen445 halamanBansal Classes Chemistry Study Material For IIT JEESankar Kumarasamy100% (4)
- Nuclear Physics Practice Problems & Reactions (40chDokumen10 halamanNuclear Physics Practice Problems & Reactions (40chChudaman MahajanBelum ada peringkat
- MCQsDokumen8 halamanMCQsFuck uBelum ada peringkat
- DPT-4 Chem & Zoo Neet 03.01.2024Dokumen8 halamanDPT-4 Chem & Zoo Neet 03.01.2024pinnaacleclasses salemBelum ada peringkat
- Xenon Chemistry Revision Sheet With AnswersDokumen4 halamanXenon Chemistry Revision Sheet With AnswersRachna JainBelum ada peringkat
- Magnetic Field Due To CurrentDokumen21 halamanMagnetic Field Due To Currentthinkiit100% (2)
- WBJEE MQB Physical Inorg Chemistry-20210701173850152602Dokumen33 halamanWBJEE MQB Physical Inorg Chemistry-20210701173850152602Sanjana DuttaBelum ada peringkat
- 7 CHEMISTRY Atomic StructureDokumen3 halaman7 CHEMISTRY Atomic StructureHasan shaikhBelum ada peringkat
- New HW Chapter 7Dokumen5 halamanNew HW Chapter 7hamadaturkman10Belum ada peringkat
- Structure of Atom - MCQsDokumen4 halamanStructure of Atom - MCQsmanish561Belum ada peringkat
- Heat TransferDokumen26 halamanHeat TransferthinkiitBelum ada peringkat
- Practice Questions For Ch. 7: Identify The Choice That Best Completes The Statement or Answers The QuestionDokumen26 halamanPractice Questions For Ch. 7: Identify The Choice That Best Completes The Statement or Answers The QuestionPaolo PepsBelum ada peringkat
- Chemical Principles 5th Edition Atkins Test BankDokumen15 halamanChemical Principles 5th Edition Atkins Test BankRobertSmithfpdzw100% (16)
- WBJEE MQB Physical Inorg Chemistry 1-20210703175752204159Dokumen33 halamanWBJEE MQB Physical Inorg Chemistry 1-20210703175752204159PRIYANSHBelum ada peringkat
- No Ans Regular Assignment of Atomic Structure XI Chapter 2Dokumen4 halamanNo Ans Regular Assignment of Atomic Structure XI Chapter 2manojwarlaniBelum ada peringkat
- JEE Atomic Structure Formula SheetsDokumen11 halamanJEE Atomic Structure Formula SheetsbsarkarBelum ada peringkat
- Race-26 - Atomic StructureDokumen3 halamanRace-26 - Atomic StructureItish maanBelum ada peringkat
- CLASS 11 CHEMISTRY MCQ CHAPTER Structure of AtomDokumen24 halamanCLASS 11 CHEMISTRY MCQ CHAPTER Structure of Atomsriram.j.athreyaBelum ada peringkat
- Modern PhysicsDokumen28 halamanModern PhysicsShubham KarandeBelum ada peringkat
- Chemistry Exam 1Dokumen6 halamanChemistry Exam 1jshalda1Belum ada peringkat
- ENEL2PAH1 - Physical Electronics 1Dokumen5 halamanENEL2PAH1 - Physical Electronics 1qanaqBelum ada peringkat
- 1 Atomic Structure PDFDokumen20 halaman1 Atomic Structure PDFanilkumarsharma1969Belum ada peringkat
- Hsslive-Xi-Chem-Prvs-Qn-2. Structure of Atom Q & ADokumen13 halamanHsslive-Xi-Chem-Prvs-Qn-2. Structure of Atom Q & Aaromalssatheesh02Belum ada peringkat
- Chemistry Revision SheetDokumen65 halamanChemistry Revision Sheetadvaitkshirasgar786Belum ada peringkat
- Premier Institute for the preparation of IIT-JEE / AIPMT chemistry homeworkDokumen9 halamanPremier Institute for the preparation of IIT-JEE / AIPMT chemistry homeworkUday Prakash SahuBelum ada peringkat
- Chapter 4 Exam Review KEYDokumen14 halamanChapter 4 Exam Review KEYERVIN DANCABelum ada peringkat
- MCQ AssignmentDokumen4 halamanMCQ AssignmentKamal KishoreBelum ada peringkat
- BS109 Sem-1 Feb 2022Dokumen4 halamanBS109 Sem-1 Feb 2022Mohammad NadirBelum ada peringkat
- CH 7 PTDokumen14 halamanCH 7 PTaaron.hartmanBelum ada peringkat
- Jee Mains 2009 Question PaperDokumen28 halamanJee Mains 2009 Question PaperYASHBelum ada peringkat
- Chapter 7 Practice Test AtomStrctrPeriodicTrend GOOD-KEY1Dokumen5 halamanChapter 7 Practice Test AtomStrctrPeriodicTrend GOOD-KEY1Senthereng MoaisiBelum ada peringkat
- Inorganic Chap#3 And#4 Hom Take ExamDokumen22 halamanInorganic Chap#3 And#4 Hom Take Examwold100% (1)
- Sample Paper - Sat: Time: 1:00 Hours Each Question Carries One MarkDokumen9 halamanSample Paper - Sat: Time: 1:00 Hours Each Question Carries One MarkAmit GuptaBelum ada peringkat
- Assignment 1 AtomicDokumen7 halamanAssignment 1 AtomicAman9692Belum ada peringkat
- Unit 1 Chapter 3 ReviewDokumen8 halamanUnit 1 Chapter 3 ReviewUday Prakash SahuBelum ada peringkat
- Chemistry Practice PaperDokumen7 halamanChemistry Practice PaperUmang ChapranaBelum ada peringkat
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesDari EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesBelum ada peringkat
- Introduction to Non-Linear Mechanics. (AM-11), Volume 11Dari EverandIntroduction to Non-Linear Mechanics. (AM-11), Volume 11Belum ada peringkat
- Answers to Selected Problems in Multivariable Calculus with Linear Algebra and SeriesDari EverandAnswers to Selected Problems in Multivariable Calculus with Linear Algebra and SeriesPenilaian: 1.5 dari 5 bintang1.5/5 (2)
- Workbook to Accompany Physics for Students of Science and EngineeringDari EverandWorkbook to Accompany Physics for Students of Science and EngineeringBelum ada peringkat
- A Course of Mathematics for Engineers and ScientistsDari EverandA Course of Mathematics for Engineers and ScientistsBelum ada peringkat
- De Moiver's Theorem (Trigonometry) Mathematics Question BankDari EverandDe Moiver's Theorem (Trigonometry) Mathematics Question BankBelum ada peringkat
- Trigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsDari EverandTrigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsPenilaian: 5 dari 5 bintang5/5 (1)
- 16 - Biomolecules (New) PDFDokumen16 halaman16 - Biomolecules (New) PDFthinkiitBelum ada peringkat
- 13 - Alcohol, Phynol, Ether (New) PDFDokumen37 halaman13 - Alcohol, Phynol, Ether (New) PDFthinkiit100% (2)
- 15 Probability PDFDokumen16 halaman15 Probability PDFthinkiit100% (2)
- 14 - Linear Programming PDFDokumen13 halaman14 - Linear Programming PDFthinkiitBelum ada peringkat
- 10 - Areas of Bounded Regions PDFDokumen8 halaman10 - Areas of Bounded Regions PDFthinkiitBelum ada peringkat
- 13 - Three-Dimensional Geometry PDFDokumen20 halaman13 - Three-Dimensional Geometry PDFthinkiitBelum ada peringkat
- 12 Vectors PDFDokumen14 halaman12 Vectors PDFthinkiitBelum ada peringkat
- 7 - Continuity and Differentiability PDFDokumen16 halaman7 - Continuity and Differentiability PDFthinkiitBelum ada peringkat
- 11 - Differential Equations PDFDokumen9 halaman11 - Differential Equations PDFthinkiitBelum ada peringkat
- 17 - Polymers (New) PDFDokumen17 halaman17 - Polymers (New) PDFthinkiit100% (3)
- 9 Integrals PDFDokumen19 halaman9 Integrals PDFthinkiitBelum ada peringkat
- 3 - Relations and Functions PDFDokumen21 halaman3 - Relations and Functions PDFthinkiit100% (1)
- 8 - Applications of Derivatives PDFDokumen15 halaman8 - Applications of Derivatives PDFthinkiitBelum ada peringkat
- 6 Determinants PDFDokumen11 halaman6 Determinants PDFthinkiitBelum ada peringkat
- 14 - Aldehydes, Ketones and Carboxylic Acids (New) PDFDokumen33 halaman14 - Aldehydes, Ketones and Carboxylic Acids (New) PDFthinkiit67% (3)
- 5 Matrices PDFDokumen14 halaman5 Matrices PDFthinkiitBelum ada peringkat
- 2 - Inverse Trigonometic FunctionsDokumen19 halaman2 - Inverse Trigonometic FunctionsHarsh RaviBelum ada peringkat
- Surface ChemistryDokumen12 halamanSurface ChemistryMecho HillBelum ada peringkat
- 18 - Chemistry in Everyday Life (New) PDFDokumen17 halaman18 - Chemistry in Everyday Life (New) PDFthinkiit60% (10)
- 15 - Amines (New) PDFDokumen25 halaman15 - Amines (New) PDFthinkiitBelum ada peringkat
- 11 - Co - Ordination Compounds PDFDokumen24 halaman11 - Co - Ordination Compounds PDFthinkiit100% (1)
- 12 - Haloareans and Halo Alkanes (New) PDFDokumen14 halaman12 - Haloareans and Halo Alkanes (New) PDFthinkiit100% (1)
- 9 - P-Block Elements PDFDokumen27 halaman9 - P-Block Elements PDFthinkiit86% (7)
- 6 - Chemical Kinetics PDFDokumen16 halaman6 - Chemical Kinetics PDFthinkiit100% (1)
- 10 - D - and F - Block Elements PDFDokumen18 halaman10 - D - and F - Block Elements PDFthinkiit100% (19)
- 8 - General Principles & Processes of Elements PDFDokumen12 halaman8 - General Principles & Processes of Elements PDFthinkiitBelum ada peringkat
- 5 - Electrochemistry PDFDokumen15 halaman5 - Electrochemistry PDFthinkiit100% (1)
- 3 - Solid State PDFDokumen15 halaman3 - Solid State PDFthinkiitBelum ada peringkat
- 4 Solution PDFDokumen14 halaman4 Solution PDFthinkiitBelum ada peringkat
- 10 - Communication Systems PDFDokumen12 halaman10 - Communication Systems PDFthinkiitBelum ada peringkat
- B Force On A Moving Charge MC Questions PDFDokumen7 halamanB Force On A Moving Charge MC Questions PDFLynn Hollenbeck BreindelBelum ada peringkat
- Historical Development of The Atom by Calvin O. DavidDokumen24 halamanHistorical Development of The Atom by Calvin O. Davidgilbert datuBelum ada peringkat
- Physics FieldsDokumen731 halamanPhysics FieldsDaisyBelum ada peringkat
- CH08 PDFDokumen25 halamanCH08 PDFpestaBelum ada peringkat
- Integralcalcvol ExfinDokumen1 halamanIntegralcalcvol ExfinMaria Deborah BaluranBelum ada peringkat
- Tangential and Normal Components AnalysisDokumen15 halamanTangential and Normal Components AnalysisOmar DoskyBelum ada peringkat
- Physics 110A: Electromagnetism: 1 Introduction and OverviewDokumen4 halamanPhysics 110A: Electromagnetism: 1 Introduction and OverviewJoshua LinBelum ada peringkat
- Atomic Structure 1Dokumen5 halamanAtomic Structure 1api-489824458100% (1)
- 6 Electronic SpectroscopyvDokumen19 halaman6 Electronic SpectroscopyvKeri Gobin SamarooBelum ada peringkat
- Hilton H. - Plane Algebraic CurvesDokumen410 halamanHilton H. - Plane Algebraic CurvesFyodor ZakBelum ada peringkat
- Strauss PDEs Section 1.1 Exercise 1Dokumen37 halamanStrauss PDEs Section 1.1 Exercise 1maria100% (2)
- Anika Et Al. - 2020 - Roughness Effect in An Initially Laminar Channel FDokumen26 halamanAnika Et Al. - 2020 - Roughness Effect in An Initially Laminar Channel FOliver HouBelum ada peringkat
- (I. Ciufolini, V. Gorini, U. Moschella, P Fre) Gra PDFDokumen422 halaman(I. Ciufolini, V. Gorini, U. Moschella, P Fre) Gra PDFprivateBelum ada peringkat
- Check If A Year Is Leap Year or Not: C++ Program To Display Fibonacci SeriesDokumen4 halamanCheck If A Year Is Leap Year or Not: C++ Program To Display Fibonacci SeriesMitesh VyasBelum ada peringkat
- Quantum Markov Modeling For Healthcare: Carla Silva, Marcus Dahlem, Ins DutraDokumen4 halamanQuantum Markov Modeling For Healthcare: Carla Silva, Marcus Dahlem, Ins DutraAdam MamboBelum ada peringkat
- Green's Functions in Mathematical PhysicsDokumen10 halamanGreen's Functions in Mathematical PhysicsZow NiakBelum ada peringkat
- SRT 8Dokumen3 halamanSRT 8Jeisson VanegasBelum ada peringkat
- Incompatible Mode AbaqusDokumen7 halamanIncompatible Mode AbaqusXuandung VuBelum ada peringkat
- If Y Is A Proper Finite Dimensional Subspace of Normed Space X, Then Dist (X, Y) 1Dokumen3 halamanIf Y Is A Proper Finite Dimensional Subspace of Normed Space X, Then Dist (X, Y) 1Rishabh SarmaBelum ada peringkat
- 2017HIT121 Supplementary QuestionsDokumen2 halaman2017HIT121 Supplementary QuestionsKeith Tanaka MagakaBelum ada peringkat
- Section 1: Introduction To VectorsDokumen4 halamanSection 1: Introduction To Vectorslupus359Belum ada peringkat
- First Year Calculus: WwlchenDokumen15 halamanFirst Year Calculus: WwlchennigerianhacksBelum ada peringkat
- 03.3. Keseimbangan Partikel IIDokumen11 halaman03.3. Keseimbangan Partikel IIBagus PerdanaBelum ada peringkat
- ch02 2Dokumen7 halamanch02 2Siow Shung Churn75% (4)
- The Following Are The Scientist Who Discover The Big Bang TheoryDokumen3 halamanThe Following Are The Scientist Who Discover The Big Bang TheoryFrances Nicole ArceBelum ada peringkat
- 3 Applications of Partial Differentiation: 3.1 Stationary PointsDokumen29 halaman3 Applications of Partial Differentiation: 3.1 Stationary PointsJustin Lansa BoyleBelum ada peringkat
- Non Linear Dynamics PDFDokumen8 halamanNon Linear Dynamics PDFMukesh KarunanethyBelum ada peringkat
- PQT Chapter 2 - Atomic Structure - Part 1Dokumen12 halamanPQT Chapter 2 - Atomic Structure - Part 1Vũ Nguyễn QuangBelum ada peringkat
- 4 Jacob Lewis Bourjaily: Q D W DDokumen2 halaman4 Jacob Lewis Bourjaily: Q D W DNori FuentesBelum ada peringkat