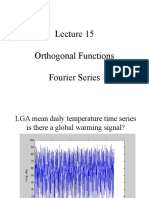
Lecture 4 - Solving dierential equations

dy
dt
+ p(t)y = g(t)
In the previous lectures, we learned to solve dierential equations of the form
dy
dt
= ay b. If we allow
nonconstant functions in the place of constants a and b, then we get equations of the form
dy
dt
= p(t)y + g(t) and these can, of course, be easily rearranged into the form
dy
dt
+ p(t)y = g(t). In this
lecture, we will learn to solve dierential equations of this form. This will allow us to obtain a solution to
the dierential equation concerning electrical circuits we encountered at the end of the previous lecture.
The key to solving dierential equations of this form will be the the product rule of derivatives. The
product rule tells us how to nd the derivative of a function when it is a product of two functions and we
already know the derivatives of both of them. Let us recall the product rule.
Product Rule of Derivatives:
If f(t) = g(t)h(t), then
df
dt
=
dg
dt
h(t) + g(t)
dh
dt
Slogan: derivative of rst second + rst derivative of second
It follows from the product rule that:

dg
dt
h(t) + g(t)
dh
dt
dt = g(t)h(t) + C.
Problem: Solve the dierential equation
dy
dt
+
1
2
y =
1
2
e
t/3
,
and nd lim
t
y.
Solution: As in the method to solve equations of the form
dy
dt
= ay b, we need to manipulate our
dierential equation into a form where we can integrate both sides! The trick here will be to nd a function
(t) such that when we multiply every term of our equation by (t)
dy
dt
(t) +
1
2
y(t) =
1
2
(t)e
t/3
we will be able to integrate the left hand side using the product rule as above!
Notice that IF it so happens that
d
dt
=
1
2
(t), then the left side is the result of the product rule!
We get:

dy
dt
(t) +
1
2
y(t) dt =

dy
dt
(t) + y
d
dt
dt = y(t) + C.
The right side integration is straightforward.
Step 1: Find the dierential equation for (t).
d
dt
=
1
2
(t)
Step 2: Solve the equation to nd (t).
We already learned to solve equations of this kind:
d
dt
(t)
=
1
2

d
dt
(t)
dt =

1
2
dt
ln|(t)| =
1
2
t + E
|(t)| = Fe
t/2
(t) = Ge
t/2
Since such a (t) will work for ANY G, we might as well pick the G that gives us the simplest expression,
namely G = 1.
(t) = e
t/2
Step 3: Multiply both sides of the equation by (t) = e
t/2
.
dy
dt
e
t/2
+
1
2
e
t/2
y =
1
2
e
t/3
e
t/2
=
1
2
e
5t/6
1
2
Step 4: Integrate both sides!

dy
dt
e
t/2
+
1
2
e
t/2
y dt =

1
2
e
5t/6
dt
Right side:

1
2
e
5t/6
dt =
1
2

6
5
e
5t/6
+ C =
3
5
e
5t/6
+ C
Left side:

dy
dt
e
t/2
+
1
2
e
t/2
y dt = ye
t/2
+ D
So ye
t/2
+ D =
3
5
e
5t/6
+ C.
Step 5: Solve for y.
ye
t/2
=
3
5
e
5t/6
+ E
y =
3
5
e
5t/6
+ E
e
t/2
=
3
5
e
t/3
+ Ee
t/2
y =
3
5
e
t/3
+ Ee
t/2
It remains to nd lim
t
3
5
e
t/3
+ Ee
t/2
.
As t , the term Ee
t/2
0.
So lim
t
3
5
e
t/3
+ Ee
t/2
= lim
t
3
5
e
t/3
= .
Problem: Solve the dierential equation
t
dy
dt
+ 2y = 4t
2
,
with the initial condition y(1) = 2.
Solution:
First we notice that the equation is not in the form
dy
dt
+ p(t)y = g(t). So we need to perform algebraic
manipulations to bring it into that form.
Step 0: Bring the equation into the form
dy
dt
+ p(t)y = g(t).
dy
dt
+
1
t
2y =
1
t
4t
2
(t = 0)
The condition t = 0 will be important to the nal solution!
dy
dt
+
2
t
y = 4t
Step 1: Find the dierential equation for (t).
dy
dt
(t) + y
d
dt
= (t)4t
dy
dt
(t) +
2
t
y(t) = (t)4t
So
d
dt
=
2
t
(t).
Step 2: Solve the equation to nd (t).
The equation
d
dt
=
2
t
(t) does NOT have the form y

= ay b because a is not constant! But nevertheless

the same method works for equations of the form y

= p(t)y as well. It only fails to work once we add a

nonzero g(t) term!
d
dt
(t)
=
2
t

d
dt
(t)
dt =

2
t
dt
ln|(t)| + C = 2 ln|t| + D
ln|(t)| = 2 ln|t| + E = ln|t|
2
+ E
e
ln |(t)|
= e
ln |t|
2
+E
|(t)| = e
ln |t|
2
e
E
= F|t|
2
= Ft
2
(t) = Gt
2
Choosing G = 1 as before, we get:
(t) = t
2
3
Step 3: Multiply both sides of the equation by (t) = t
2
.
dy
dt
t
2
+
2
t
t
2
y = t
2
4t
dy
dt
t
2
+ 2ty = 4t
3
Step 4: Integrate both sides!

dy
dt
t
2
+ 2ty dt =

4t
3
dt
Right side:

4t
3
dt = t
4
+ C
Left side:

dy
dt
t
2
+
2t
y
dt = yt
2
+ D
So yt
2
+ D = t
4
+ C.
Step 5: Solve for y.
yt
2
= t
4
+ E
y =
t
4
+ E
t
2
y = t
2
+ E/t
2
(t = 0)
The restriction t = 0 comes from the beginning of the problem!
Finally, we solve for E using the initial condition y(1) = 2.
y(1) = 1
2
+ E/1
2
= 1 + E = 2
E = 1
y = t
2
+ 1/t
2
(t > 0)
The reason we impose the restriction t > 0 instead of t = 0 is that we always want a solution on an interval
of the line including our initial condition. Our initial condition is t = 1 and we know that t = 0. So the
interval t > 0 is the maximum chunk of the line avoiding the forbidden value of t and including the initial
condition.
Problem: Solve the dierential equation
dy
dt
2y = 4 t,
and nd lim
t
y.
Solution:
Step 1: Find the dierential equation for (t).
dy
dt
(t) + y
d
dt
= (t)(4 t)
dy
dt
(t) 2y(t) = (t)(4 t)
Therefore
d
dt
= 2(t).
Step 2: Solve the equation to nd (t).
d
dt
(t)
= 2

d
dt
(t)
dt =

2 dt
(t) = Ge
2t
Choosing G = 1 as before, we get:
(t) = e
2t
Step 3: Multiply both sides of the equation by (t) = e
2t
.
dy
dt
e
2t
2e
2t
y = e
2t
(4 t)
Step 4: Integrate both sides!

dy
dt
e
2t
2e
2t
y dt =

e
2t
(4 t) dt
Right side: we use integration by parts.
4
Let us briey review where the formula for integration by parts comes from.

f(t)g

(t) + f

(t)g(t) dt = f(t)g(t)

f(t)g

(t) dt +

f

(t)g(t) dt = f(t)g(t)
Integration by Parts formula:

f(t)g

(t) dt = f(t)g(t)

(t)g(t) dt

e
2t
(4 t) dt:
f(t) = 4 t g

(t) = e
2t
f

(t) = 1 g(t) =
1
2
e
2t

e
2t
(4 t) dt =
1
2
e
2t
(4 t)

1
2
e
2t
dt =
1
2
e
2t
(4 t)
1
2
(
1
2
e
2t
) =
1
2
e
2t
(4 t) +
1
4
e
2t
+ C
Left side:

dy
dt
e
2t
2e
2t
(t)y dt = ye
2t
+ D
So ye
2t
+ D =
1
2
e
2t
(4 t) +
1
4
e
2t
+ C
Step 5: Solve for y.
ye
2t
=
1
2
e
2t
(4 t) +
1
4
e
2t
+ E
y =

1
2
e
2t
(4 t) +
1
4
e
2t
+ E
e
2t
y =
1
2
(4 t) +
1
4
+ Ee
2t
=
1
2
4 +
1
2
t +
1
4
+ Ee
2t
=
7
4
+
1
2
t + Ee
2t
y =
7
4
+
1
2
t + Ee
2t
It remains to nd lim
t

7
4
+
1
2
t + Ee
2t
.
If E > 0, then lim
t

7
4
+
1
2
t + Ee
2t
=
if E < 0, then lim
t

7
4
+
1
2
t + Ee
2t
=
if E = 0, then y =
7
4
+
1
2
t and lim
t

7
4
+
1
2
t =
General Formula:
Solve
dy
dt
+ p(t)y = g(t).
Step 1: Find the dierential equation for (t).
dy
dt
(t) +
d
dt
y = g(t)
dy
dt
(t) + p(t)(t)y = g(t)(t)
So
d
dt
= p(t)(t).
Step 2: Solve the equation to nd (t).
d
dt
(t)
= p(t)

d
dt
(t)
dt =

p(t) dt
ln|(t)| + C =

p(t) dt
ln|(t)| =

p(t) dt + D
(t) = e
R
p(t) dt+D
= e
D
e
R
p(t) dt
= Ee
R
p(t) dt
The simplest possible such (t) has E = 1.
So we chose:
(t) = e
R
p(t) dt
Step 3: Multiply both sides of the equation by (t) = e
R
p(t) dt
.
dy
dt
e
R
p(t) dt
+ e
R
p(t) dt
p(t)y = e
R
p(t) dt
g(t)
Step 4: Integrate both sides!
5

dy
dt
e
R
p(t) dt
+ e
R
p(t) dt
p(t)y dt =

e
R
p(t) dt
g(t) dt
ye
R
p(t) dt
+ C =

e
R
p(t) dt
g(t) dt
Step 5: Solve for y.
ye
R
p(t) dt
=

e
R
p(t) dt
g(t) dt + D
y =

e
R
p(t) dt
g(t) dt
e
R
p(t) dt
+
D
e
R
p(t) dt
Problem: Solve the dierential equation
2
dy
dt
+ ty = 2,
with the initial condition y(0) = 1.
Solution: First we need to bring the equation into the form
dy
dt
+ p(t)y = g(t).
dy
dt
+
t
2
y = 1
Using the general formula:
(t) = e
R
t/2 dt
= e
t
2
/4
y =

e
t
2
/4
dt
e
t
2
/4
+
E
e
t
2
/4
y = e
t
2
/4
(

e
t
2
/4
dt + E)
So it remains to nd

e
t
2
/4
dt, but the problem is that the antiderivative of e
t
2
/4
is not expressible in
terms of the standard functions that we operate with. Therefore the function F(t) =

e
t
2
/4
dt can only be
approximated numerically! But even to approximate it numerically we MUST have some bounds on the
integral (see Lecture 1)!
From the problem, we have an initial condition for y and this will give us bounds for the integral! Let us
see how.
y = e
t
2
/4
(F(t) + E) (F(t) =

e
t
2
/4
dt)
y(0) = e
0
(F(0) + E) = F(0) + E = 1
E = 1 F(0)
y = e
t
2
/4
(F(t) + 1 F(0))
y = e
t
2
/4
(F(t) F(0) + 1)
But F(t) F(0) =

t
0
e
s
2
/4
ds!
Notice that we changed the variable under the integral from t to s. The reason for that is very simple:
otherwise t is used in too many places and it gets confusing. Once you have a denite integral (meaning it
has bounds), you can use any letter to designate the independent variable of the function you are
integrating because the end result is a number anyway.
y = e
t
2
/4
(

t
0
e
s
2
/4
ds + 1)
For example: y(5) = e
25/4
(

5
0
e
s
2
/4
ds + 1) where we will use areas of rectangles to approximate the
integral

5
0
e
s
2
/4
ds.