www.jntuworld.

com

www.jwjobs.net

Analog Communications

Unit 4
Lecture Notes 30

Spectrum Analysis of sinusoidal FM wave

The FM wave for sinusoidal modulation is given by

s (t ) = Ac cos[2f c t + sin 2f m t ]

(1)

Using a well-known trigonometric identity, we may expand this relation as

s (t ) = Ac cos(2f c t ) cos[ sin( 2f m t )] Ac sin( 2f c t ) sin [ sin( 2f m t )]

(2)

From this expanded from, we see that the in-phase and quadrature components of the FM
waves s(t) for the case of sinusoidal modulation are as follows.
s1 (t ) = Ac cos[ sin 2f m t ]

(3)

s Q (t ) = Ac sin [ sin 2f m t ]

(4)

Hence, the complex envelope of the FM wave equals

s1 (t ) = s1 (t ) + js Q (t )
= Ac exp[J sin (2f m t )]

(5)

The complex envelope s(t) retains complete information about the modulation process.
Indeed, we may readily express the FM wave s(t) in terms of the complex envelope s(t)
by writing
s (t ) = Re[ Ac exp( j 2f c t ) + j sin( 2f m t )]
= Re[s (t ) exp( j 2f c t

)]

(6)

T. Kalpana,ECE,GMRIT

www.jntuworld.com

www.jntuworld.com

www.jwjobs.net

Analog Communications

Unit 4
Lecture Notes 30

From Eq 5, the complex envelope is a periodic function of time, with a fundamental

frequency equal to the modulation frequency f m .Therefore it can be expanded as the
form of a complex Fourier series as follows

s (t ) =

exp( j 2nf m t )

(7)

n =

Where the complex Fourier coefficient Cn equals

cn = f m

12 f
m
1
2 fm

s (t ) exp( j 2nf m t ) dt

12 f
m
c
1
2 fm

= fm A

(8)
exp[ j sin( 2nf m t ) j 2 n f m t ] dt

For convenience, we define the variable

x = 2f m t

(9)

In terms of which we may rewrite Eq 8 as

cn =

Ac
2

exp[ j( sin x nx )] dx

(10)

The integral on the right side of Eq 10 is recognized as the nth order Bessel function of
the first kind and argument . This function is commonly denoted by the symbol Jn()
that is

cn =

1
2

exp[ j( sin x nx )] dx

T. Kalpana,ECE,GMRIT

www.jntuworld.com

(11)

www.jntuworld.com

www.jwjobs.net

Analog Communications

Unit 4
Lecture Notes 30

Hence, we may rewrite Eq 10 as

c n = Ac j n ( )

(12)

Substituting Eq 12 in 7 , we get, in terms of the Bessel function Jn(), the following

expansion for the complex envelope of the FM wave

s (t ) = Ac

j ( ) exp( j 2nf t )
n

(13)

n =

Next, substituting Eq 13 in eq.6, we get

s (t ) = Ac Re j n ( ) exp[ j 2 ( f c + nf m )t ]
n =

(14)

Interchanging the order of summation and evaluating the real part of the right side of Eq
14, we get

s (t ) = Ac j n ( ) cos[2 ( f c + nf m )t ]
n=

(15)

This is the desired from for the Fourier series representation of the single-stone FM wave
s(t) for an arbitrary value of . The discrete spectrum of s(t) is obtained by taking the
Fourier transforms of both sides of Eq (15)thus

S(f)=Ac

j ( ) [( ( f f
n

nf m ) +( ( f + f c + nf m ) ]

(16)

n =

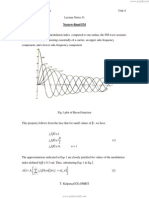
Fig.1 shows the plot between the Bessel function versus the modulation index for n 0, 1,
2, 3, 4. These plots show that for fixed n, alternates between positive and negative values

T. Kalpana,ECE,GMRIT

www.jntuworld.com

www.jntuworld.com

www.jwjobs.net

Analog Communications

Unit 4
Lecture Notes 30

for increasing and that approaches zero as approaches infinity. Note also that for fixed
we have

J-n() = Jn(),

n even

J-n() = - Jn()

n odd

Accordingly, we need only plot or tabulate for positive values of order n.

Fig 1 Plots of Bessels function of first kind

T. Kalpana,ECE,GMRIT

www.jntuworld.com