Part 1 PARTIAL DERIVATIVES

MAT 295

Chapter 8

Extremum of
Functions
At the end of this chapter, students should be able to:

Define, compute and classify critical points for a function of two variables

Define and compute the relative extrema for a function of two variables

Solve applied extrema problems

8.1 Introduction
In earlier chapter the discussion involved application of partial derivatives. In
chapter 7, problems such as determining the slope of the tangent line at a
point (a, b) and rate at which a volume of certain object change as the
dimension changed were look into.
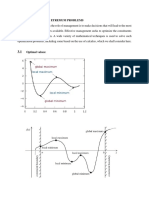
In chapter 8, another application of partial derivatives will be explored. Refer
to Figure 8.1, the graph consist of high and low points. Among the higher and
lower points, it is possible to have the highest and lowest point among all
points. What are these points and how can they be located? To answer this
question an understanding of the critical point and the extremum for a function
of a single variable is required.

103

Part 1 PARTIAL DERIVATIVES

MAT 295

Figure 8.1: Graph for function of two variables

8.2 Critical Points

Note that for a function of single variable f (x ) , a critical point is a point at
which the slope of the tangent line of the function is either zero or undefined.
In other words at critical points the tangent line is horizontal to x-axis
and f ' ( x )

dy
0 (Figure 8.2).
dx
y

Figure 8.2: At critical points the tangent line of f (x ) is horizontal

In this section the critical points for a function of two variables f ( x, y ) will be
identified and later classify them in section 8.3. A critical point is also known
as a stationary point.

Definition
Let f ( x, y ) be a function of two variables. A point (a, b) is a critical point of
f ( x, y ) if either

(a)

f x a, b 0 and fy a, b 0 or

(b)

f x a, b 0 or fy a, b does not exist.

104

Part 1 PARTIAL DERIVATIVES

MAT 295

Since the function f ( x, y ) consist two independent variables then in order to

compute the critical point it is necessary to determine the first order partial
derivatives with respect to both independent variables. Similar to function of a
single variable the partial derivatives of f ( x, y ) is either zero or is undefined
and this implies that at the critical point the tangent plane is horizontal.

Steps
Find f x and fy
Let f x 0 and fy 0

Solve f x 0 and fy 0 simultaneously

Determine the critical point(s)
Integrate simplify problem

Example 1
Find the critical point(s) for the function f ( x, y ) 4xy 2x 2 y .

Solution

Find f x and fy
f x 4y 4 x

(1)

fy 4 x 1

(2)

The function will have a critical point if fx fy 0 or one of these partial

derivatives does not exist.

Let fx 0 and fy 0
f x 4y 4 x 0

fy 4 x 1 0

Solve fx 0 and fy 0 simultaneously

f x 4y 4 x 0
yx

4x 1 0
1
x
4

Determine the critical points

105

Part 1 PARTIAL DERIVATIVES

Then compute the corresponding value for y.

x

1
:
4

1
4

1 1
Therefore the critical point is ,
.
4 4

Example 2
Find the critical points for the function f ( x, y ) 3 4xy 2x 2 y 3 .

Solution

Find f x and fy
f x 4y 4 x

(1)

f y 4 x 3y 2

(2)

Let fx 0 and fy 0
fy 4 x 3y 2 0

f x 4y 4 x 0

Solve fx 0 and fy 0 simultaneously

fx 4y 4 x 0
y x

4 x 3y 2 0
4x 3x 2 0
x 4 3 x 0
x 0 @

4
3

Determine the critical points

x 0:
x

4
:
3

y 0
y

(0, 0)

4
3

4 4
,

3 3

4 4
Therefore the critical points are 0, 0 and ,
.
3 3

Example 3
Find the critical point(s) for the function
f ( x, y ) 2x 3 y 3 3x 2 18y 2 81y 5 .

106

MAT 295

Part 1 PARTIAL DERIVATIVES

MAT 295

Solution

fx 6x 2 6x

(1)

fy 3y 2 36 y 81

(2)

The critical points exist if fx fy 0 or one of these partial derivatives

does not exist. Now solve (1) and (2) simultaneously.
6x 2 6x 0
6 x x 1 0
x 0 @

x 1

and
3y 2 36 y 81 0
y 2 12 y 27 0

y 9y 3 0
y 9

y 3

The solutions, which are the critical points to the above system of
equations are given by 0, 3 , 0, 9 , 1, 3 and 1, 9 .

Warm up exercise
3

Let f ( x, y ) 3y x y 3x :
(i)

find f x and fy .

(ii)

solve fx 0 and fy 0 simultaneously.

(iii)

identify the critical point(s).

8.3 Extremum
Once the critical points of a function f ( x, y ) are identified, how can they be
classified? Recall that the critical point(s) of a function of a single variable
f (x ) can be classified as relative minimum, relative maximum or inflection

point by applying the first and second derivatives tests. Similarly, the critical

107

Part 1 PARTIAL DERIVATIVES

MAT 295

point(s) of a function of two variables can be classified as relative minimum,

relative maximum or saddle point.

Definition
A function f of two variables is said to have a relative maximum at a point
(a, b) if for all point ( x, y ) sufficiently close to (a, b) such that f (a, b) f ( x, y ) .

Definition
A function f of two variables is said to have a relative minimum at a point
(a, b) if for all point ( x, y ) sufficiently close to (a, b) such that f (a, b) f ( x, y ) .

Definition
A function f of two variables is said to have a saddle point at (a, b) if the
function f has neither a relative minimum nor a relative maximum point.

Minimum point

Maximum point

Saddle point

Figure 8.3: Extremum

The classification can be done by applying a second partial derivative test for
functions of two variables.

Definition

The term D D(a, b) f xx (a, b)fyy (a, b) f xy (a, b) 2 is called the discriminant
of the function f ( x, y ) .

108

Part 1 PARTIAL DERIVATIVES

MAT 295

Theorem
Second Partial Derivatives Test
Suppose the second partial derivatives of f are continuous on critical point
(a, b), and suppose that f x (a, b) 0 and fy (a, b) 0 . Let

D(a, b) f xx (a, b)fyy (a, b) f xy (a, b) 2

a)

If D 0 and f xx (a, b) 0 , then f has a relative minimum at (a, b) .

b)

If D 0 and f xx (a, b) 0 , then f has a relative maximum at (a, b) .

c)

If D 0 , then f has a saddle point at (a, b) .

d)

If D 0 , then the test is inconclusive.

Steps
Identify the critical point(s) (a, b) of f
Find f xx , fyy , and fxy

At each critical point (a, b) evaluate

o f xx (a, b)
o fyy (a, b)
o

f xy (a, b) I

Compute the discriminant value

D(a, b) f xx (a, b)fyy (a, b) f xy (a, b) 2

Check D and f xx (a, b) (if necessary)
Classify as minimum, maximum, saddle point or
no conclusion

Example 4
The critical points for the function f ( x, y ) 3 4xy 2x 2 y 3 are 0, 0
4 4
and ,
. Classify the critical point(s).
3 3

Solution

Identify the critical point(s) (a, b)

0, 0 and 4 ,
3

Find f xx , fyy , and fxy

fyy 6y
f xx 4
109

f xy 4

Part 1 PARTIAL DERIVATIVES

At each critical point (a, b) evaluate

(0, 0)

4 4
,

3 3

f xx (a, b)

fyy (a, b)

f xy (a, b)

-16

4 4
,

3 3

16

Check D and f xx (a, b) (if necessary)

(0, 0)

4 4
,

3 3

<0

> 0

Not
f xx (a, b)

necessary

>0

to check

Classify as minimum, maximum, saddle point or no conclusion

4 4
,

(0, 0)
3 3
Conclusion

Saddle point

Relative
minimum

Example 5
Locate and classify the critical point for f ( x, y ) 3x 2 2xy y 2 8y .

Solution

Compute the discriminant value D(a, b) f xx (a, b)fyy (a, b) f xy (a, b) 2

(0, 0)

MAT 295

Identify the critical point(s) a, b

f ( x, y ) 3 x 2 2 xy y 2 8 y
f x 6 x 2y
fy 2 x 2y 8

110

Part 1 PARTIAL DERIVATIVES

MAT 295

To determine the critical point(s) of f

f x 6 x 2y 0
y 3x
fy 2 x 2y 8 0

(1)

2 x 2(3 x ) 8
4x 8
x2

Replacing x 2 into (1) yields y 6 . Therefore the critical point is (2, 6).

Find f xx , fyy , and fxy

fxx 6

fyy 2
f xy 2

At critical point evaluate

Critical point

(2, 6)

fxx 6

fyy 2

f xy 2

-2

2
(a, b)
Compute discriminant D f xx (a, b)fyy (a, b) f xy

Critical point

(2, 6)

D f xxfyy f xy 2

Check D and f xx (a, b) (if necessary)

Critical point

D f xxfyy f xy 2

(2, 6)
>0

Classify as minimum, maximum, saddle point or no conclusion

Critical point

(2, 6)

Conclusion

Minimum

Example 6
Locate all relative extremum and saddle points of f ( x, y ) x 3 y 3 3xy .

111

Part 1 PARTIAL DERIVATIVES

MAT 295

Solution

f ( x, y ) x 3 y 3 3xy
fx 3 x 2 3y
fy 3 y 2 3 x

To determine the critical point(s) of f

fx 3 x 2 3y 0
y x 2

(1)

fy 3 y 2 3 x 0
3( x 2 )2 3 x 0
x4 x 0
x (1 x 3 ) 0
x 0 @ x 1

Replacing

x 0 and

x 1 into (1) yields

y 0 and y 1

Therefore the critical points are (0, 0) and (1, -1).

Compute the 2nd derivatives to determine the discriminant.
f xx 6 x

fyy 6y
f xy 3

To determine the extremum and saddle points apply the second partial
derivative test.

Critical point

(0, 0)

f xx 6 x

fyy 6y

f xy 3

2
D f xx (a, b)fyy (a, b) f xy
(a, b)

Conclusion

-9
Saddle point

112

(1, -1)

27
Minimum point

Part 1 PARTIAL DERIVATIVES

MAT 295

Example 7
Find the stationary point(s) and determine the nature of the point(s) if
f ( x, y ) 2x 3 6xy 2 3y 3 150 x .

Solution

f ( x, y ) 2 x 3 6 xy 2 3 y 3 150 x
f x 6 x 2 6 y 2 150
f y 12 xy 9 y 2

To determine the critical point(s)

f x 6 x 2 6 y 2 150 0
6 x 2 6 y 2 150
y 2 25 x 2

(1)

fy 12 xy 9 y 2 0

3 y 4 x 3 y 0
y 0

Replacing y 0 and y
y 0

or

4x
into (1) yields
3

25 x 2 0

4x
3

x 5

4x
16 x 2
: 25 x 2
3
9

25

25 x 2
0
9

5 x
5x

5
5
0
3
3

x 3
x 3 :
x 3 :

or

x 3

y 4
y 4

Therefore the critical points are (5, 0), (-5, 0), (3, 4), and (-3, -4). Then
compute the second partial derivatives to determine the determinant
f xx 12 x

fyy 12 x 18 y

f xy 12y

To determine the extremum and saddle points apply the second partial
derivative test.

113

Part 1 PARTIAL DERIVATIVES

Critical point

(5, 0)

(-5, 0)

(3, 4)

(-3, -4)

fxx 12x

60

-60

36

-36

fyy 12 x 18 y

60

-60

-36

36

f xy 12y

48

-48

3600

3600

-3600

-3600

Min

Max

Saddle

Saddle

D f xxfyy f xy 2

Conclusion

MAT 295

Example 8
Find all the critical points of the function f ( x, y ) 4xy x 4 y 4 . Determine
which give relative minima, relative maxima or saddle points.

Solution

Find the critical point(s).

fx 4y 4 x 3 0
y x3

(1)

4 x 1 x 1 x 1 x 0
4 x 1 x 1 x 1 x 1 x 0
4x 1 x 4 1 x 4 0

fy 4 x 4y 3 0
4 x 4( x 3 )3 0
4x 4x 9 0

4x 1 x 8 0

x 0

or

x 1

or

x 1

or

x i

Replacing the critical numbers into ( 1) yields

x 0:

y 0

x 1 :

y 1

x 1:

y 1

Therefore the critical points are (0, 0), (1, 1) and (-1, -1).
f xx 12x 2

fyy 12y 2

fxy 4

To determine the extremum or saddle points apply the second partial

derivative test.

114

Part 1 PARTIAL DERIVATIVES

MAT 295

Critical point

(0, 0)

(1, 1)

(-1, -1)

f xx 12x 2

-12

-12

fyy 12y 2

-12

-12

fxy 4

-16

128

128

Saddle

Maximum

Maximum

D f xxfyy f xy 2

Conclusion

Warm up exercise
Classify the given critical points for the function f ( x, y ) .
Critical point

(0, 0)

(2, 1)

,2
3

1
,1
3

fxx 6 x

fyy 2y
f xy 2

D fxxfyy fxy 2

Conclusion

8.4 Applied Extremum Problems

The extremum problems can be used to solve applied problems involving
more than one independent variable. In this section, an example of these
problems will be discussed.

115

Part 1 PARTIAL DERIVATIVES

MAT 295

Steps
Identify the unknown (variables)
Determine the function f ( x, y ) to represent the
problem
Find f x , fy to identify the critical number

Find f xx , fyy , and fxy to determine the value of

the discriminant
Check the discriminant and f xx (if necessary)
Conclude

Example 9
A rectangular box open at the top is to have a volume of 32 cm3 . What
must be the dimensions so that the total surface is minimum?

Solution

Identify the unknown (variables)

L length

w width

h height

V volume

S total surface

Determine the function S( x, y ) to represent the problem

h
w
L
Figure 8.4 : A rectangular box open at the top
Volume V Lwh 32
32
L
wh
Surface S h, L, w Lw 2Lh 2wh
32
32

w 2
h 2wh
wh
wh
32 32
S h, w 2 2wh
h w

Find Sh , Sw to identify the critical number(s)

64
2h
S w
w2

116

(1)

Part 1 PARTIAL DERIVATIVES

32
2w
Sh
h2

MAT 295

(2)

Determine the critical point(s)

To determine critical number from (1)
64

2h 0
w2
32
h
w2

then replace into (2)

w4

2w 0
32

w 4 64w 0

w w 3 64 0

w w 4 w 2 4w 16 0

Therefore the real critical numbers are w 0 @ w 4 . But the

possible width is w 4 . Hence, determine h and L.
w 4:

and

L4

Compute Sww , Shh , and Swh to determine the discriminant

Sww

h2

128
w

Shh

64
h3

Swh 2

Check discriminant and Shh (if necessary)

D ShhSww Swh 2
(8)(2) (2)2
12 0

Conclude

Since D 0 the computed dimensions will produce a minimum total

surface for the open rectangular box.

Example 10
Find the dimensions of a six-faced box that has the shape of a rectangular
prism with the largest possible volume that you can make with 12 square
meters of cardboard.

117

Part 1 PARTIAL DERIVATIVES

MAT 295

Solution

Using all available cardboard to make the box, the total area A of all six
faces of the prism is given by
A 2xy 2yz 2zx 12

The volume V of the box is given by

V xyz

Solve the equation 2xy 2yz 2zx 12 for z

z

6 xy
xy

Substitute z in the expression of the volume V to obtain.

6 xy

V ( x, y ) xy
xy

Let us find the critical points by first finding the first order partial derivatives
Vx ( x, y )

Vx ( x, y )

y 2 x 2 2xy 6

x y

x 2 y 2 2xy 6

x y

We now solve the system of equations given by Vx 0 and Vy 0 . One

obvious solution is given by the point (0,0) but is not physically possible.
Other solutions are found by setting
x 2 2xy 6 0 and y 2 2xy 6 0

Subtracting the equations term by term we obtain

x2 y 2 0

Solve to obtain
x y and x y

The solution x y is not valid for this problem since both x and y are
dimensions and cannot be negative. Use x y in the equation
x 2 2xy 6 0 ,

we obtain x 2 2x 2 6 0 .
Solve for x
x 2
118

Part 1 PARTIAL DERIVATIVES

MAT 295

Find y
y 2

Let us now find the second order partial derivatives

Vxx ( x, y )

Vyy ( x, y )

2y 2 y 2 6

x y

2x 2 x 2 6

x y

Vxy ( x, y )

2xy x 2 3 xy y 2 6

x y

We now need the values of Axx , Ayy , and Axy to find the value of
D Vxx

2, 2 Vyy

2, 2 Vxy

2, 2

in order to use the theorem on minima and maxima of functions with 2

variables.
D Vxx

2, 2 Vyy 2, 2 Vxy2

D is positive and Vxx

2, 2

5
2

2, 2 2 is negative and therefore the volume V

is maximum for
x 2 meters
y 2 meters
z

6 xy
2 meters
xy

Warm up exercise
A prism is to have a volume of 50cm3 . What must be the dimensions so
that the total surface is minimum?
(i) Identify the variables.
(ii) Determine a suitable function.
(iii) Compute the critical number and discriminant.
(iv) Conclude your answer.

119

Part 1 PARTIAL DERIVATIVES

MAT 295

Exercise 8

1.

Determine the critical point(s) of the functions. Hence, investigate the nature of
the critical points.
a) f ( x, y ) 3y x 3 y 3 2x
b) f ( x, y ) x 3 y 3 2x 6y
c) f ( x, y ) x 2 xy 2y x 1
d) f ( x, y ) x 2 8x 5y 2 10y 13

2.

Locate all relative extremum and/or saddle point(s) of

a) f ( x, y ) 9 x 2 y 2
b) f ( x, y ) x 2 4xy y 2 6y
c) f ( x, y ) 4xy x 4 y 4
d) f ( x, y ) 3x 2 2xy y 2 8y
e) f ( x, y ) y 2 x 2
f) f ( x, y ) 3xy 6x 3y 7
g) f ( x, y ) ( x 2)2 ( y 1)2
h) f ( x, y ) x 2y 5
i) f ( x, y ) x 2 y 2
j) f ( x, y ) e xy

3.

Find the dimension of a closed rectangular box of minimum surface area that
has a volume of 100 cm3.

4.

Suppose that we want to design a building with a rectangular shape having a

volume of 147,840 meter3. Assuming that the daily loss of heat from the building
is given by 11xy 14yz 15 xz , where x,y and z are the length, width and the
height of the building respectively, find the dimension for which the daily heat
loss is minimal. (Hint: xyz 147,840 )

5.

Find three numbers x, y and z such that their sum is 30 and their product is a
maximum.

120