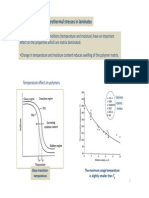
Composites
Diunggah oleh
DEEPAKHak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Composites
Diunggah oleh
DEEPAKHak Cipta:
Format Tersedia
S I T ES G
CO
OU
4.1
SI
T
EN
TE
U NI
R
4.
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
Y OF
Classical lamination theory
4.1. Introduction
Chapter 2 and 3 focused on the behaviour of a single layer. The thermomechanical properties of such a layer can be predicted, and the stress-strain
relationship is known. This will now be extended to the more general case of a
laminated plate. The most common type of analysis will be developed next, and is
known as the classical lamination theory. This plane stress theory makes it
possible to relate external loads (in-plane forces and moments) to the composite
plate deformations.
The analysis of laminates will first be introduced by considering the behaviour of
simple laminated beam under pure bending.
4.2. La mi nated bea ms i n pure be nding
Considering laminated beams under pure flexural loading gives an introduction to
the more general laminated plate theory. Elementary principles of mechanics of
material applied for beam calculations will be used here. We will focus on the
main differences occurring with isotropic beams.
A rectangular laminated beam of thickness h and width b is subjected to a bending
moment M, which is constant over the whole length of the beam (pure bending).
The beam is made of N layers. As
shown in fig. 4.1, the position of a
layer k in the beam is defined by
the distances zk-1 and zk. It is worth
emphasising that these distances
are taken from the middle axis of
the beam and not from the neutral
d
axis.
The following assumptions are
taken:
z0
1
a. The plies are perfectly bonded
z
1
2
M
h/2
ne
together.
-pla
m id
zk
b. Plane cross-sections which are
M
zk-1
x
initially perpendicular to the
h
k
longitudinal axis of the beam
n
remain plane and normal
during flexure.
z
c. Each ply behaves linear
elastically with no in-plane
dx
shear coupling ([C16]=0)
We will add for simplicity that the
beam has geometrical and property fig. 4.1: Composite beam bending with layer
numbering system
symmetry about the middle axis.
fig. 4.1 shows a beam element of length dx subjected to a moment M and
therefore having a radius of curvature and an angle between the normals to the
beam axis d. From assumption (b), an expression for the longitudinal strain at a
distance z from the middle axis is:
S I T ES G
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
CO
OU
U NI
E
SI
T
EN
TE
4.2
Y OF
( + z ) d d
z
(4.1)
d
According to assumption (c), the longitudinal stress at a distance z from the
middle axis becomes:
z
x = Ex
(4.2)
Static equilibrium gives an expression for the bending moment:
x =
M =
b z dz
(4.3)
By taking into account the stress xk and elasticity modulus E xk in each layer k,
we obtain:
zk
N
b z2
b N k 3
E x (zk 1 zk3 )
M = E xk
dz =
(4.4)
k =1 zk 1
k =1
The bending moment can also be expressed as a function of the elasticity modulus
of the laminated beam E xl :
E xl I y
with I y = b z 2 dz
(4.5)
With Iy the moment of inertia with respect to the y-axis. From (4.4) and (4.5), an
expression for the elasticity modulus of the beam can be obtained:
b N k 3
E xl =
E x (z k 1 z k3 )
(4.6)
3 I y k =1
Using this expression, it is possible to obtain expressions for the deflection of
laminated beams from elementary mechanics of material.
Expression for the stress in the kth layer xk can be written by eliminating in
relations (4.2) and (4.5):
M z E xk
xk =
(4.7)
I y E xl
1
This relation for the stress is similar to the one used for isotropic
2
beam, corrected by the dimensionless term in bracket. The stress
3
is therefore a discontinuous function of the beam depth, in
x
contrast to the stress in an isotropic beam. An example of a stress
profile of a symmetric 6 layers beam subjected to a bending
moment, where E x2 > E 1x = E x3 is given in fig. 4.2.
fig. 4.2: Example of a
M=
stress profile of a beam
beam subjected to a
bending moment.
S I T ES G
CO
OU
4.3
U NI
E
SI
T
EN
TE
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
Y OF
4.3. Theor y of la mi nated plates
The more general case of a
1
z0=-1/2 h
laminated plate under plane
zk-1
stress condition will now be
1*
analysed. In-plane loading (axial
and shear) will be considered as
k
x
loading, as well as moments 2*
0
(bending and torsion). As for the
2
laminated beam, the layers are y
assumed bonded together. No
zn=1/2 h
restriction is set on the lay-up
used, which means that various
n
coupling effects will be present.
Coupling effects mean that an
3
in-plane stress applied to a
3* z
laminated plate may result in a
complex
combination
of
x,y,z:
Laminate CS
extensional,
flexural
and
(at mid-plane)
torsional deformations. The
1*,2*,3: Layer CS
different notations are defined in
1,2,3:
Material CS (at )
fig. 4.3. This figure also defines
the different coordinate systems.
fig. 4.3: The different coordinate systems used in the
The position of the layers in the laminated plate theory
normal direction is defined with
the mid-plane as a reference (and
not the neutral plane).
The assumptions relevant for the analysis are similar to the one used for the beam
analysis and can be translated to:
a. The displacements u, v, w corresponding to the directions x, y and z are small
compared to the plate thickness h. The displacement u and v are a linear
function of the depth z (plane cross-sections which are initially perpendicular
to the longitudinal axis of the plate remain plane and normal during
deformation)
b. Transverse shear strains and normal strain are negligible.
4.3.1. Strain in a layer k
According to assumption (a), in-plane displacements are a linear function of the
depth z. Both can be expressed with the displacement in the middle surface (u0
and v0) as reference:
u = u 0 ( x, y ) + z f u ( x, y )
v = v 0 ( x, y ) + z f v ( x , y )
(4.8)
w = w 0 ( x, y) = w( x, y)
Normal strain is negligible (assumption (b)) and the normal (or transverse)
displacement w is constant for any coordinate (x,y). According to the same
assumption, transverse shear strains are negligible and can be used in the strain-
S I T ES G
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
CO
OU
U NI
E
SI
T
EN
TE
4.4
Y OF
displacement relations in order to find an expression for fu and fv. The strain in a
layer and in its coordinate system (1*, 2*, 3) can be written as:
v w
w
w
4* =
+
= f v ( x, y ) +
= 0 f v ( x, y ) =
z y
y
y
(4.9)
u w
w
w
5* =
+
= f u ( x, y ) +
= 0 fu ( x, y ) =
z x
x
x
Using the expressions for the in-plane displacements (4.8), the in-plane strains
are:
u u 0
2w
2w
=
z 2 = x0 z 2
x
x
x
x
0
2
v v
w
2w
2* =
=
z 2 = y0 z 2
y y
y
y
1* =
6* =
(4.10)
u v u 0 v 0
2w
2w
+
=
+
2z
= xy0 2 z
y x y
x
xy
xy
With x0 , 0y , xy0 the in-plane strains in the mid-plane. It can be shown from
geometrical considerations that:
x =
2w
2w
2w
; y = 2 ; xy = 2
2
x
y
xy
(4.11)
with the plate curvature (1/). The equation (4.10) relates the strain in a layer
with quantities related to the laminate: the mid-plane strain and the curvature.
4.3.2. Stress-strain relationship of a layer k
An expression for the stress in the kth layer as a function of the mid-plane strain
and the plate curvature is obtained by combining (4.10) with the relation (3.27)
obtained in chapter 3. In matrix form, this can be written as:
{ *}k = [C*]k { 0 } + z[C*]k { }
(4.12)
4.3.3. Laminate loading-deformation relations
External forces and moments acting on a laminated plate can be related to the
stress in the layer, and then to the laminate deformation. For example, the axial
forces Nx per unit width can be obtained by summing the axial stresses x acting
on each layer:
N zk
N x = ( 1* ) k dz
k =1 z k 1
(4.13)
where (1*)k is the stress in the kth layer in the 1* direction (layer coordinate
system). A similar expression can be written for the normal force in the
y-direction as well as for the in-plane shear force Nxy. Substituting (4.12) in the
force resultants gives in matrix form:
S I T ES G
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
CO
OU
U NI
E
SI
T
EN
TE
4.5
Y OF
{N } =
k =1
{N } =
k =1
zk
([ C *] k { 0 } + z [C *] k { }) dz
z
k 1
zk
zk
[C *] k { 0 } dz + [C *] k { } zdz
z k 1
z k 1
(4.14)
1 N
{ N } = [C *] k ( z k z k 1 ) { 0 } + [C *] k ( z k2 z k21 ) { }
k =1
2 k =1
This is mostly rewritten in the following way:
Nx
Ny =
N
xy
A11
sym
A12
A22
A16 x0
A26 0y +
A66 xy0
B11
sym
B12
B 22
B16 x
B26 y
B66 xy
(4.15)
The A-matrix is also called the laminate extensional stiffness matrix, is symmetric
and its components are defined as:
Aij =
k =1
(C ij *) k ( z k z k 1 )
(4.16)
The B-matrix is called the laminate coupling stiffness matrix, is symmetric and its
components are defined as:
Bij =
1 N
(C ij *) k ( z k2 z k2 1 )
2 k =1
(4.17)
A similar development can be performed for the moment resultants. This gives as
end result the following relations:
Mx
My =
M
xy
B11
sym
B12
B22
B16 x0
B26 0y +
B66 xy0
D11
sym
D12
D 22
D16 x
D 26 y
D 66 xy
(4.18)
The B-matrix is also present here. The D-matrix is called the laminate bending
stiffness matrix, is symmetric and its components are defined as:
Dij =
1 N
(C ij *) k ( zk3 zk3 1 )
3 k =1
(4.19)
The relations (4.15) and (4.18) are often written in partitioned form:
N A
=
M B
B 0
D
(4.20)
Although the three components of the 'ABD' matrix have similar appellations
(stiffness), they have distinct units. As loading is mostly expressed "per unit
width" (force resultants N in N/m and moments M in N), the A-components have
for unit N/m, the B-components in N and the D-components in Nm.
S I T ES G
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
CO
OU
U NI
E
SI
T
EN
TE
4.6
Y OF
4.3.4. Inversion of the laminate loading-deformation relations
Inversion of relation (4.20) is often necessary, as the loading is generally known,
and not the other way around. This can be done by simply inverting the [ABD]
matrix as a whole. However, performing the inversion by inverting the sub
matrices A, B and D can be interesting for particular laminate lay-up. The result is
then of the form:
0
=
a
b T
b N
d M
(4.21)
For example, it can be shown that the extensional compliance matrix [a] can be
written:
[ a ] = [ A]1 + [ A]1 [ B ] ([ D ] [ B ] [ A] 1 [ B ]) [ B ] [ A] 1
1
(4.22)
This relation reduces for to [A]-1 when the components of the [B]-matrix are zero
(laminate is symmetric). Components of the [b]- and [d]-matrix can be evaluated
as follow:
[b ] = [ A]1 [ B ] ([ D ] [ B ] [ A]1 [ B ])
[ d ] = ([ D ] [ B ] [ A]1 [ B ])
(4.23)
Similarly to the [A]-matrix, the inverted bending stiffness [d] components can be
calculated by directly inverting the [D]-matrix only if the components of the [B]matrix are zero. It is worth adding that the coupling compliance matrix [b] is not
symmetric. The relation between the curvature vector {} and the force vector
{N} is defined by the transposed of the [b]-matrix.
4.4.
Proble ms
4.1
Derive for the [ABD]-matrix for 2 laminates [-45/45]s (symmetric) and
[-45/45/-45/45] (antisymmetric) based on 1mm thick layers of Carbon-PEI
having the following layer properties:
E1=120GPa, E2=8GPa, G12=3,5GPa, 12=0.3
In which [ABD] terms do these two lay-up differ, and what does this mean?
4.2
Give on the next figure the physical signification of the following stiffnessmatrix terms:
A16 and A26; B11, B22 and B12, B16 and B26, B66, D16 and D26
S I T ES G
Composites Course 2008-2009 University of Twente, Eng. & Tech.
4. Classical lamination theory - Laurent Warnet & Remko Akkerman.
CO
OU
SI
T
EN
TE
U NI
R
Y OF
x0
0
y
xy0
=
x
y
xy
a11
a
21
a 61
b11
b12
b16
a12
a 22
a 62
b21
b22
b26
a16
a 26
a 66
b61
b62
b66
b11
b21
b61
d 11
d 21
d 61
b12
b22
b62
d 12
d 22
d 62
b16 N x
b26 N y
b66 N xy
d 16 M x
d 26 M y
d 66 M xy
4.7
Anda mungkin juga menyukai
- Shoe Dog: A Memoir by the Creator of NikeDari EverandShoe Dog: A Memoir by the Creator of NikePenilaian: 4.5 dari 5 bintang4.5/5 (537)
- Genetic AlgorithmDokumen16 halamanGenetic AlgorithmHemanthKumarBelum ada peringkat
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDari EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifePenilaian: 4 dari 5 bintang4/5 (5794)
- H 406 6 HygrothermalDokumen21 halamanH 406 6 HygrothermalHemanthKumarBelum ada peringkat
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDari EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RacePenilaian: 4 dari 5 bintang4/5 (895)
- H 406 2 UnidiretionalDokumen17 halamanH 406 2 UnidiretionalHemanthKumarBelum ada peringkat
- The Yellow House: A Memoir (2019 National Book Award Winner)Dari EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Penilaian: 4 dari 5 bintang4/5 (98)
- AE1101 Intro 2Dokumen14 halamanAE1101 Intro 2HemanthKumarBelum ada peringkat
- Grit: The Power of Passion and PerseveranceDari EverandGrit: The Power of Passion and PerseverancePenilaian: 4 dari 5 bintang4/5 (588)
- AE1101 Intro 4Dokumen73 halamanAE1101 Intro 4HemanthKumar100% (1)
- The Little Book of Hygge: Danish Secrets to Happy LivingDari EverandThe Little Book of Hygge: Danish Secrets to Happy LivingPenilaian: 3.5 dari 5 bintang3.5/5 (400)
- Introduction To Aerospace Engineering: Lecture SlidesDokumen56 halamanIntroduction To Aerospace Engineering: Lecture SlidesHemanthKumarBelum ada peringkat
- The Emperor of All Maladies: A Biography of CancerDari EverandThe Emperor of All Maladies: A Biography of CancerPenilaian: 4.5 dari 5 bintang4.5/5 (271)
- AE1101 Intro 1Dokumen20 halamanAE1101 Intro 1HemanthKumarBelum ada peringkat
- Never Split the Difference: Negotiating As If Your Life Depended On ItDari EverandNever Split the Difference: Negotiating As If Your Life Depended On ItPenilaian: 4.5 dari 5 bintang4.5/5 (838)
- RBEsDokumen94 halamanRBEsSteli IvanBelum ada peringkat
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDari EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyPenilaian: 3.5 dari 5 bintang3.5/5 (2259)
- AE1110x 5a SlidesDokumen13 halamanAE1110x 5a SlidesHemanthKumarBelum ada peringkat
- On Fire: The (Burning) Case for a Green New DealDari EverandOn Fire: The (Burning) Case for a Green New DealPenilaian: 4 dari 5 bintang4/5 (74)
- En 015 09Dokumen20 halamanEn 015 09HemanthKumarBelum ada peringkat
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDari EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FuturePenilaian: 4.5 dari 5 bintang4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDari EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryPenilaian: 3.5 dari 5 bintang3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnDari EverandTeam of Rivals: The Political Genius of Abraham LincolnPenilaian: 4.5 dari 5 bintang4.5/5 (234)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDari EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaPenilaian: 4.5 dari 5 bintang4.5/5 (266)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDari EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersPenilaian: 4.5 dari 5 bintang4.5/5 (345)
- The Unwinding: An Inner History of the New AmericaDari EverandThe Unwinding: An Inner History of the New AmericaPenilaian: 4 dari 5 bintang4/5 (45)
- Rise of ISIS: A Threat We Can't IgnoreDari EverandRise of ISIS: A Threat We Can't IgnorePenilaian: 3.5 dari 5 bintang3.5/5 (137)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDari EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You ArePenilaian: 4 dari 5 bintang4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Dari EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Penilaian: 4.5 dari 5 bintang4.5/5 (121)
- Her Body and Other Parties: StoriesDari EverandHer Body and Other Parties: StoriesPenilaian: 4 dari 5 bintang4/5 (821)