Prediction On House Asking Price in Jinjang
Diunggah oleh
sadyehclenJudul Asli
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Prediction On House Asking Price in Jinjang
Diunggah oleh
sadyehclenHak Cipta:
Format Tersedia
UECM2263 Applied Statistical Models, January 2016
Assignment Report 1
UTAR, Malaysia
Lecturer: Dr. Chang Yun Fah
PREDICTION ON HOUSE ASKING PRICE IN JINJANG
Sutha Kathiravan1, Keoy Eng Chiew2, Chin Yan3, Sathya Seelan1, Liaw Zhen Liang1
1
AS, Y2S2, Department of Mathematics and Actuarial Sciences, UTAR
FM, Y2S1, Department of Mathematics and Actuarial Sciences, UTAR
AM, Y2S2, Department of Mathematics and Actuarial Sciences, UTAR
sutha_sky@yahoo.com
Abstract Statistical research was carried out
on houses pending for sale in Jinjang, Kuala
Lumpur in order to determine the housing
affordability and other information that are
relevant for potential buyers to know. This will
ensure that house hunters are able to make good
decisions when choosing a house through our
statistical findings. Key word: statistics
I.
INTRODUCTION
This project is a research on the factors affecting
the houses up for sale in Jinjang. Researches in
Malaysia currently say that even though the
economy is slowing and the value of ringgit
Malaysia is depreciating but economists say that
the price of the houses continue to rise. Making it
difficult for Malaysians to own a house in the
future.[2]
Through our project, we have identified 13
predictor variables: We want to investigate what are
the Area, Housing Type, Land area, Built-up area,
Tenure type, Number of bedroom, Number of
bathroom, Furnished, Distance to nearest
LRT/KTM/Monorail station, Distance to nearest
primary school, Distance to nearest secondary
school, Distance to nearest shopping mall, and
Distance to nearest mosque. Plus, and a response
variable (Asking price of the property). We
collected data from a website (iProperty) and then
conducted statistical analysis on it using Rprogram. In this project, we do not use area and
land area as predictor variable because they are not
related. Distance to nearest mosque also not used
because there are too many missing value.
The variables we will be using are defined as
follow:
+6011-26169767
* X2 is the Built-up Area.
* X3 is the Tenure Type.
* X4 is the Number of Bedroom.
* X5 is the Number of Bathroom.
* X6 is the Distance to the nearest
LRT/KTM/Monorial station.
* X7 is the Distance to the nearest primary school.
* X8 is the Distance to the nearest secondary school
* X9 is the Distance to nearest shopping mall/
convenience store
* X10 is the Furnished.
The significance level that we will use throughout
this project is =0.05.
II.
Methodology
We carried out our project on houses that were up
for sale in Jinjang, Kuala Lumpur through
iProperty. Our population is Jinjang and our sample
consists of 65 observations.
Firstly, we suggest a multi-linear regression model
to explain the relationship between the response
variable Y, and the predictor variables. Under this
hypothesis,
Y= 0 + 1X1 + 2X2 + B3X3 + 4X4 + 5X5 +
6X6 + 7X7 + 8X8 + 9X9 + 10X10 +
III.
Analysis and Discussion
Residuals:
Min
1Q Median
* Y is the Asking Price.
-532028 -101390
* X1 is the Housing Type
Coefficients:
3Q
Max
2596 135809 427012
UECM2263 Applied Statistical Models, January 2016
Assignment Report 1
UTAR, Malaysia
Lecturer: Dr. Chang Yun Fah
Estimate Std. Error t value Pr(>|t|)
3.
4.
5.
6.
(Intercept) 79525.93 156095.35 0.509 0.61250
X1
99512.34 59918.18 1.661 0.10255
X2
220.92
53.87 4.101 0.00014 ***
The error term has constant variance.
The errors are normally distributed.
The error are uncorrelated.
No outliers.
The validity of these assumptions should always be
doubtful and conduct analysis to examine the
adequacy of model. The residual vs x is examine
the linearity for a model while the residual vs
predicted value is measure the constancy of the
variance. Normal probability plot is measure
whether the error is normally distributed or not. In
this assignment we are going to check X2 (Built-up
Area) and X4 (Number of Bedroom) as the others
variables are not related.
X3
***
-262283.09 63980.86 -4.099 0.00014
X4
***
83774.21 16884.73 4.962 7.34e-06
X5
109262.42 45492.11 2.402 0.01979 *
X6
-67520.15 39347.29 -1.716 0.09189 .
X7
-130055.64 84225.01 -1.544 0.12839
X8
31032.78 75666.86 0.410 0.68334
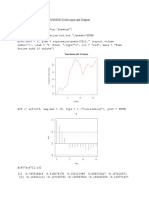
Residual VS Built-Up Area
X9
50432.54 49294.02 1.023 0.31082
Input
X10
106441.45 130001.33 0.819 0.41652
Non-linearity of Regression Model
model.reg<-lm(Y~X2,data=model.dat)
Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
0.1 1
plot(x=model.dat$X2, y=model.reg$residuals, xlab
= "Built-Up Area", ylab = "Residuals",
main="Residuals vs. Built-Up Area", col = "red",
pch =
19,cex=1.5,panel.first=grid(col="gray",lty="dotted
"))
Residual standard error: 230400 on 54 degrees of
freedom
abline(h=0,col="blue")
Multiple R-squared: 0.7909, Adjusted R-squared:
0.7522
Output
---
F-statistic: 20.43 on 10 and 54 DF, p-value:
5.681e-15
After analyzing the data to find the summary of
each variables, we have found that the fitted
regression equation is
= 79525.93 + 99512.34X1 + 220.92X2
262283.09X3 + 83774.21X4+ 109262.42X5
67520.15X6 - 130055.64X7 + 31032.78X8 +
50432.54X9 + 106441.45X10
Model Adequancy Checking
Assumptions:
1.
2.
The relationship between the response Y
and the predictor variables are linear.
The error term, has zero mean.
Figure 1: The residuals fall within a horizontal
band centred around 0, displaying no systematic
tendencies to be positive and negative. Therefore,
linear regression model is appropriate.
Residual VS Bedrooms
model.reg<-lm(Y~X4,data=model.dat)
plot(x=model.dat$X4, y=model.reg$residuals, xlab
= "Bedrooms", ylab = "Residuals",
main="Residuals vs. Bedrooms", col = "red", pch =
UECM2263 Applied Statistical Models, January 2016
Assignment Report 1
Lecturer: Dr. Chang Yun Fah
19,cex=1.5,panel.first=grid(col="gray",lty="dotted
"))
abline(h=0,col="blue")
UTAR, Malaysia
Residual VS Bedrooms
Input
model.reg<-lm(Y~X4,data=model.dat)
plot(x=model.reg$fitted.values,
y=model.reg$residuals, xlab = "Bedrooms", ylab =
"Residuals", main="Residuals vs. Predicted
Values", col = "red", pch =
19,cex=1.5,panel.first=grid(col="gray",lty="dotted
"))
abline(h=0,col="blue")
Output
Figure 2: The residuals fall within a horizontal
band centred around 0, displaying no systematic
tendencies to be positive and negative. Therefore,
linear regression model is appropriate.
Non-constancy of Error Variance
Residual VS Built-Up Area
Input
model.reg<-lm(Y~X2,data=model.dat)
plot(x=model.reg$fitted.values,
y=model.reg$residuals, xlab = "Built-Up Area",
ylab = "Residuals", main="Residuals vs. Predicted
Values", col = "red", pch =
19,cex=1.5,panel.first=grid(col="gray",lty="dotted
"))
abline(h=0,col="blue")
Output
Figure 4: The graph shown that all points are
randomly scatted within a horizontal band centred
and no funnel shape is observed. Hence, constant
variance assumption seems to be fulfilled.
Normal Probability Plot
Price vs Built-Up Area
Input
model.reg<-lm(Y~X2,data=model.dat)
qqplot<qqnorm(model.reg$residuals,main="Normal
Probability Plot",xlab="Built-up
Area",ylab="Price",plot.it=TRUE ,col="blue",
pch=19,
cex=1.5,panelfirst=grid(col="gray",lty="dotted"))
abline(lm(qqplot$y~qqplot$x))
Figure 3: The graph shown that all points are
randomly scatted within a horizontal band centered
and no funnel shape is observed. Hence, constant
variance assumption seems to be fulfilled.
UECM2263 Applied Statistical Models, January 2016
Assignment Report 1
UTAR, Malaysia
Lecturer: Dr. Chang Yun Fah
Output
the error of all regressors conform to the normality
assumption initially made. No violation of
normality is detected.
According to [3], it says here that the interior
designs do affect the pricing of the house due the
number of bathrooms, bedrooms and the housing
type apart from its geographical location.
Coefficient of Determination
model
R.sq
adj.R.sq
Figure 5.From the graph above, error terms do not
depart substantially from normality suggesting that
the error of all regressors conform to the normality
assumption initially made. No violation of
normality is detected.
x1
0.1331626
0.1194033
x1, x2
0.5943963
0.5813123
x1, x2, x3
x1, x2, x3, x4
Referring to [1], research has shown that built-up
affects according to its location. If it is rural, the
housing price should be lower but if the it is located
in a city with a large built-up area, dwellers would
show in favour of those kind of houses.
x1, x2, x3, x4,x5
0.7551079
0.7343543
x1,x2,x3,x4,x5,x6
0.7769258
0.7538492
x1,x2,x3,x4,x5,x6,x7
0.7831864
0.7565602
x1,x2,x3,x4,x5,x6,x7,x8
0.7832118
0.7522420
x1,x2,x3,x4,x5,x6,x7,x8,x9
0.7883409
0.7537057
0.7909363
0.7522208
Price vs Bedrooms
0.6297972 0.6115905
0.7343859
10 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10
0.7166783
Input
model.reg<-lm(Y~X4,data=model.dat)
Call:
qqplot<qqnorm(model.reg$residuals,main="Normal
Probability
Plot",xlab="Bedrooms",ylab="Price",plot.it=TRUE
,col="blue", pch=19,
cex=1.5,panelfirst=grid(col="gray",lty="dotted"))
lm(formula = Y ~ X1 + X2 + X3 + X4 + X5 + X6 +
X7, data = model.dat)
abline(lm(qqplot$y~qqplot$x))
Residuals:
Min
1Q Median
3Q
Max
-534969 -81367 13282 156080 410508
Output
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 139279.00 138479.11 1.006 0.318774
X1
X2
Figure 6 From the graph above, error terms do not
depart substantially from normality suggesting that
102055.71 57921.39 1.762 0.083437 .
218.51
52.48 4.164 0.000107 ***
X3
***
-247709.72 60273.66 -4.110 0.000128
X4
81540.08 16412.54 4.968 6.5e-06 ***
UECM2263 Applied Statistical Models, January 2016
Assignment Report 1
UTAR, Malaysia
Lecturer: Dr. Chang Yun Fah
X5
**
119661.49 44113.46 2.713 0.008811
X6
-77243.87 37898.25 -2.038 0.046180 *
X7
-92439.26 72053.61 -1.283 0.204711
--Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
0.1 1
Residual standard error: 228400 on 57 degrees of
freedom
Multiple R-squared: 0.7832, Adjusted R-squared:
0.7566
F-statistic: 29.41 on 7 and 57 DF, p-value: < 2.2e16
IV.
Conclusion
As you can see the best model is model7 because
model7 has the highest adjusted R squared.
Therefore, the best model used to estimate the price
of a house is
= 139279 + 102055.71X1 + 218.51X2
247709.72X3 + 81540.08X4 + 119661.49X5
77243.87X6 92439.26X7
The challenge that we faced throughout this project
was having certain predictors corresponding with
the response variable because throughout the
process of collecting the data and compiling them,
we have found that the variable that contains the
distance to the nearest mosque has a lot of missing
variables and it became a challenge for us to do the
scatterplot. Hence, this predictor had to be ignored.
In the future, a project should be carried out where
all the predictors have values.
V.
Reference
[1] Gallent N., Shucksmith M., Tewdwr-Jones M.
(2003). Housing in the European Countryside:
Rural Pressure and Policy in Western Europe.
Architecture. 35-36
[2] Malaysias property market slowing sharply.
(2016, January 4). Global Property Guide.
Retrieved
March
23,
2016,
from
http://www.globalpropertyguide.com/Asia/malaysia
/Price-History
[3] Positive and negative impacts on house prices.
Rightmove.
Retrieved
from
http://www.rightmove.co.uk/what-affects-houseprices.html
VI. Overall
Overall, from the project that we have carried out,
we made assumptions of a multiple linear
regression models. Obtained a scatterplot to test its
validity by testing the non-linearity of regression
model and the non-constancy of error variance
between Residual vs. Built-Up Area and Residual
vs. Bedrooms; testing the Normal Probability Plot
between Price vs. Built-Up Area and Price vs.
Bedroom. The coefficient of determination was
obtained in order R square and the adjusted R
square so that the best model could be obtained.
We were able to get the best model and
was able to determine the validity of the all 7
models before choosing the best one. Hence, with
the model that we have just obtained, we could now
determine the asking price of the houses in Jinjang.
Anda mungkin juga menyukai
- Development of Robust Design Under Contaminated and Non-Normal DataDokumen21 halamanDevelopment of Robust Design Under Contaminated and Non-Normal DataVirojana TantibadaroBelum ada peringkat
- Clay 2017Dokumen13 halamanClay 2017everst gouveiaBelum ada peringkat
- Econometric Model With Cross-Sectional, Time Series, and Panel DataDokumen4 halamanEconometric Model With Cross-Sectional, Time Series, and Panel DataDian KusumaBelum ada peringkat
- Chapter 8 Non-Parametric StatisticsDokumen26 halamanChapter 8 Non-Parametric Statisticstemesgen yohannesBelum ada peringkat
- Error and Uncertainty: General Statistical PrinciplesDokumen8 halamanError and Uncertainty: General Statistical Principlesdéborah_rosalesBelum ada peringkat
- QM Resit AssignmntDokumen9 halamanQM Resit AssignmntrunaBelum ada peringkat
- 6034 - Classical Linear Regression ModelDokumen30 halaman6034 - Classical Linear Regression Modelbobktg82Belum ada peringkat
- ECO 401 Model Selection and Structural BreaksDokumen31 halamanECO 401 Model Selection and Structural BreaksJerry maBelum ada peringkat
- Stat 101 Exam 1 FormulasDokumen18 halamanStat 101 Exam 1 FormulasXanh Nước BiểnBelum ada peringkat
- Unit 9Dokumen16 halamanUnit 9swingbikeBelum ada peringkat
- MicroEconometrics Lecture10Dokumen27 halamanMicroEconometrics Lecture10Carolina Correa CaroBelum ada peringkat
- A Cusp Catastrophe Model For Developing Marketing Strategies For Online Art AuctionDokumen10 halamanA Cusp Catastrophe Model For Developing Marketing Strategies For Online Art AuctionNha ReshBelum ada peringkat
- Integer Optimization and its Computation in Emergency ManagementDari EverandInteger Optimization and its Computation in Emergency ManagementBelum ada peringkat
- Devore Ch. 1 Navidi Ch. 1Dokumen16 halamanDevore Ch. 1 Navidi Ch. 1chinchouBelum ada peringkat
- Econometrics Project 2020323Dokumen7 halamanEconometrics Project 2020323usaeed alviBelum ada peringkat
- Digital Signal Processing (DSP) with Python ProgrammingDari EverandDigital Signal Processing (DSP) with Python ProgrammingBelum ada peringkat
- RegressionDokumen6 halamanRegressionRAJU SHATHABOINABelum ada peringkat
- Chapter 36 Large Sample Estimation and Hypothesis TestingDokumen135 halamanChapter 36 Large Sample Estimation and Hypothesis Testingdoanhnghiep171Belum ada peringkat
- Introductory Econometrics Exam MemoDokumen9 halamanIntroductory Econometrics Exam Memomdxful002100% (4)
- Statistics Lecture Course 2022-2023Dokumen66 halamanStatistics Lecture Course 2022-2023Cece SesBelum ada peringkat
- Business SolutionsDokumen227 halamanBusiness Solutionsoykubayraktar100% (6)
- Econ 306 HW 3Dokumen7 halamanEcon 306 HW 3PPPBelum ada peringkat
- Robust Statistics For Outlier Detection (Peter J. Rousseeuw and Mia Hubert)Dokumen8 halamanRobust Statistics For Outlier Detection (Peter J. Rousseeuw and Mia Hubert)Robert PetersonBelum ada peringkat
- Multiple RegressionDokumen7 halamanMultiple RegressionarmailgmBelum ada peringkat
- Sta. Elena College Data InterpretationDokumen40 halamanSta. Elena College Data InterpretationJohn Ericson PeñaBelum ada peringkat
- Geographically Weighted Regression: Martin Charlton A Stewart FotheringhamDokumen17 halamanGeographically Weighted Regression: Martin Charlton A Stewart FotheringhamAgus Salim ArsyadBelum ada peringkat
- Specification Testing of Production in A Stochastic Frontier ModelDokumen10 halamanSpecification Testing of Production in A Stochastic Frontier ModelMireya Ríos CaliBelum ada peringkat
- SLR Assignment1 CSDokumen3 halamanSLR Assignment1 CSTariqBelum ada peringkat
- CHAPTER 11 Chi Square and Other Non Parametric TestsDokumen77 halamanCHAPTER 11 Chi Square and Other Non Parametric TestsAyushi JangpangiBelum ada peringkat
- Module 2 in IStat 1 Probability DistributionDokumen6 halamanModule 2 in IStat 1 Probability DistributionJefferson Cadavos CheeBelum ada peringkat
- Regression and Multiple Regression AnalysisDokumen21 halamanRegression and Multiple Regression AnalysisRaghu NayakBelum ada peringkat
- Regression Analysis Engineering StatisticsDokumen72 halamanRegression Analysis Engineering StatisticsLeonardo Miguel LantoBelum ada peringkat
- Real estate value prediction using regression modelsDokumen8 halamanReal estate value prediction using regression modelsAimane CAFBelum ada peringkat
- AQM Regression Day 3 Class WorkDokumen4 halamanAQM Regression Day 3 Class Workaneeqa.shahzadBelum ada peringkat
- Economic predictions with big data: Sparse or dense modellingDokumen5 halamanEconomic predictions with big data: Sparse or dense modellingbillpetrrieBelum ada peringkat
- Experimental Modeling: Dr. G. Suresh KumarDokumen30 halamanExperimental Modeling: Dr. G. Suresh KumarShakeb RahmanBelum ada peringkat
- Error and Data AnalysisDokumen38 halamanError and Data AnalysisisiberisBelum ada peringkat
- Probability Distributions ExplainedDokumen38 halamanProbability Distributions ExplainedswingbikeBelum ada peringkat
- Evaluation of Analytical DataDokumen58 halamanEvaluation of Analytical DataJoyce Mariele RomeroBelum ada peringkat
- Basic Regression AnalysisDokumen5 halamanBasic Regression AnalysisAnantha VijayanBelum ada peringkat
- Case Reyem AffairDokumen22 halamanCase Reyem AffairVishal Bharti100% (3)
- Multiple Regression: X X, Then The Form of The Model Is Given byDokumen12 halamanMultiple Regression: X X, Then The Form of The Model Is Given byezat syafiqBelum ada peringkat
- Evans Analytics2e PPT 08Dokumen73 halamanEvans Analytics2e PPT 08qunBelum ada peringkat
- Power properties of the Sargan test with measurement errorsDokumen6 halamanPower properties of the Sargan test with measurement errorsismetgocerBelum ada peringkat
- Forecasting Cable Subscriber Numbers with Multiple RegressionDokumen100 halamanForecasting Cable Subscriber Numbers with Multiple RegressionNilton de SousaBelum ada peringkat
- S1181 U03 NotesDokumen5 halamanS1181 U03 NotesLoganHarperBelum ada peringkat
- M07 Julita Nahar PDFDokumen8 halamanM07 Julita Nahar PDFNadya NovitaBelum ada peringkat
- Nonparametric Quantile EstimationDokumen32 halamanNonparametric Quantile EstimationMannyBelum ada peringkat
- Answers Review Questions EconometricsDokumen59 halamanAnswers Review Questions EconometricsZX Lee84% (25)
- Uncertanties and Intro Pupil BookletDokumen23 halamanUncertanties and Intro Pupil Bookletapi-322008295Belum ada peringkat
- Data Visualisations TechniquesDokumen4 halamanData Visualisations TechniquesMbusoThabetheBelum ada peringkat
- Statistics Chapter 1 SummaryDokumen53 halamanStatistics Chapter 1 SummaryKevin AlexanderBelum ada peringkat
- Whittemore1997.Multistage SamplingDokumen14 halamanWhittemore1997.Multistage SamplingarmanBelum ada peringkat
- Dynamic Central Place Theory: Results Simulation Approach: Roger W. WhiteDokumen18 halamanDynamic Central Place Theory: Results Simulation Approach: Roger W. WhiteAtul Saini100% (1)
- Scientific Notation and Significant FiguresDokumen18 halamanScientific Notation and Significant FiguresLawrence AnDrew FrondaBelum ada peringkat
- Non-Linear Analysis On Exxon Mobil Share PricesDokumen12 halamanNon-Linear Analysis On Exxon Mobil Share PricesSorin George MarinBelum ada peringkat
- Coordinate Transformation Uncertainty Analysis in Large-Scale MetrologyDokumen9 halamanCoordinate Transformation Uncertainty Analysis in Large-Scale Metrologyjorge david Otalora muñozBelum ada peringkat
- Introduction To Machine Learning Week 2 AssignmentDokumen8 halamanIntroduction To Machine Learning Week 2 AssignmentAkash barapatreBelum ada peringkat
- 5.2 - Sampling Distribution of X ̅ - Introduction To Statistics-2021 - LagiosDokumen15 halaman5.2 - Sampling Distribution of X ̅ - Introduction To Statistics-2021 - LagiosAmandeep SinghBelum ada peringkat
- Learn Statistics Fast: A Simplified Detailed Version for StudentsDari EverandLearn Statistics Fast: A Simplified Detailed Version for StudentsBelum ada peringkat
- Analog Rep 2Dokumen14 halamanAnalog Rep 2sadyehclenBelum ada peringkat
- UEEA2333 Analog Electronics Tutorial SolutionsDokumen3 halamanUEEA2333 Analog Electronics Tutorial SolutionssadyehclenBelum ada peringkat
- Wa0001Dokumen27 halamanWa0001sadyehclenBelum ada peringkat
- ScheduleDokumen1 halamanSchedulesadyehclenBelum ada peringkat
- T3 FiltersDokumen2 halamanT3 FilterssadyehclenBelum ada peringkat
- Ch7 Power Amps6 v2Dokumen73 halamanCh7 Power Amps6 v2sadyehclenBelum ada peringkat
- Ch2b Data Converter v2Dokumen37 halamanCh2b Data Converter v2sadyehclenBelum ada peringkat
- Ch1 Feedback and StabilityDokumen88 halamanCh1 Feedback and Stabilitysadyehclen100% (1)
- Ch2a Op Amp v3Dokumen66 halamanCh2a Op Amp v3sadyehclenBelum ada peringkat
- Engineering and Science UEEA1333 Bachelor of Engineering (Hons) Analogue Electronics Year 1, 2 Mr. NG Choon Boon 201401Dokumen2 halamanEngineering and Science UEEA1333 Bachelor of Engineering (Hons) Analogue Electronics Year 1, 2 Mr. NG Choon Boon 201401sadyehclenBelum ada peringkat
- Ch5 Non-Linear CircuitsDokumen29 halamanCh5 Non-Linear CircuitssadyehclenBelum ada peringkat
- T3 FiltersDokumen2 halamanT3 FilterssadyehclenBelum ada peringkat
- Filters and Tuned Amplifiers DesignDokumen79 halamanFilters and Tuned Amplifiers DesignsadyehclenBelum ada peringkat
- Ch6 RegulatorsDokumen62 halamanCh6 RegulatorssadyehclenBelum ada peringkat
- Engineering and Science UEEA1333 Bachelor of Engineering (Hons) Analogue Electronics Year 1, 2 Mr. NG Choon Boon 201401Dokumen2 halamanEngineering and Science UEEA1333 Bachelor of Engineering (Hons) Analogue Electronics Year 1, 2 Mr. NG Choon Boon 201401sadyehclenBelum ada peringkat
- UTAR ANALOGUE ELECTRONICS TUTORIAL SOLUTIONSDokumen3 halamanUTAR ANALOGUE ELECTRONICS TUTORIAL SOLUTIONSsadyehclenBelum ada peringkat
- UEEA2333 Assignment 2014Dokumen3 halamanUEEA2333 Assignment 2014sadyehclenBelum ada peringkat
- T2 OpampDokumen2 halamanT2 OpampsadyehclenBelum ada peringkat
- Covyy: E Y E EyDokumen3 halamanCovyy: E Y E EysadyehclenBelum ada peringkat
- Receipt of Lab Report Submission (To Be Kept by Student)Dokumen2 halamanReceipt of Lab Report Submission (To Be Kept by Student)sadyehclenBelum ada peringkat
- T5 RegulatorDokumen3 halamanT5 RegulatorsadyehclenBelum ada peringkat
- T4 OscDokumen3 halamanT4 OscsadyehclenBelum ada peringkat
- ANALOGUE ELECTRONICS TUTORIAL QUESTIONSDokumen2 halamanANALOGUE ELECTRONICS TUTORIAL QUESTIONSsadyehclenBelum ada peringkat
- ANALYSIS OF TIME SERIES DATADokumen7 halamanANALYSIS OF TIME SERIES DATAsadyehclenBelum ada peringkat
- Pusat Bimbingan Sri Inderawasih Mathematics Form 1 Test 1: Lembaga PeperiksaanDokumen5 halamanPusat Bimbingan Sri Inderawasih Mathematics Form 1 Test 1: Lembaga PeperiksaansadyehclenBelum ada peringkat
- Paper 3 All in 1Dokumen11 halamanPaper 3 All in 1sadyehclenBelum ada peringkat
- Maths2015 SyllabusDokumen40 halamanMaths2015 Syllabuspvr2k1Belum ada peringkat
- UEMH4333 Tutorial 3Dokumen2 halamanUEMH4333 Tutorial 3sadyehclenBelum ada peringkat
- Seminar Fasa 1 - Paper 3Dokumen23 halamanSeminar Fasa 1 - Paper 3sadyehclenBelum ada peringkat
- Presentation MH BI LatestDokumen8 halamanPresentation MH BI LatestsadyehclenBelum ada peringkat
- ICMAP Syllabus 2012Dokumen33 halamanICMAP Syllabus 2012FaisalBelum ada peringkat
- Introduction To Bayesian Monte Carlo Methods in WINBUGSDokumen37 halamanIntroduction To Bayesian Monte Carlo Methods in WINBUGSrshe0025004Belum ada peringkat
- MIT18 05S14 Exam Final SolDokumen11 halamanMIT18 05S14 Exam Final SolErwin Dave M. DahaoBelum ada peringkat
- Stochastic Frontier Analysis Using Stata: 13, Number 4, Pp. 719-758Dokumen40 halamanStochastic Frontier Analysis Using Stata: 13, Number 4, Pp. 719-758Reuben RichardBelum ada peringkat
- Influence of Religion on Beliefs of PH StudentsDokumen20 halamanInfluence of Religion on Beliefs of PH StudentsMaria GonzalesBelum ada peringkat
- Lab Report ProjectDokumen8 halamanLab Report ProjectMubin Mustaza IskandarBelum ada peringkat
- Construction Tender Price IndexDokumen356 halamanConstruction Tender Price IndexSwain Niranjan100% (1)
- M818A: Machine Learning and Cyber Security-ADokumen11 halamanM818A: Machine Learning and Cyber Security-ASahag TopouzkhanianBelum ada peringkat
- Prototype Format for Action Research and InnovationDokumen3 halamanPrototype Format for Action Research and InnovationMarivic AlegriaBelum ada peringkat
- MAS KeyDokumen579 halamanMAS KeyNguyễn Ngọc PhướcBelum ada peringkat
- EBQ2024 Statistics Tutorial SolutionsDokumen5 halamanEBQ2024 Statistics Tutorial SolutionsLi YuBelum ada peringkat
- Hypothesis Testing With One SampleDokumen16 halamanHypothesis Testing With One SampleAlexa LeeBelum ada peringkat
- The Effects of Technology Use in Relation To The Critical Thinking Skills of The Grade 11 StudentsDokumen52 halamanThe Effects of Technology Use in Relation To The Critical Thinking Skills of The Grade 11 StudentsVhon CruzBelum ada peringkat
- Establishing Causality Is Difficult, Whether Conclusion...Dokumen3 halamanEstablishing Causality Is Difficult, Whether Conclusion...Anas JamshedBelum ada peringkat
- Lee Et Al, 2021Dokumen31 halamanLee Et Al, 2021imam santosaBelum ada peringkat
- Montgomery Design and Analysis of Experiments Wiley 2012Dokumen757 halamanMontgomery Design and Analysis of Experiments Wiley 2012Manan Vaja100% (4)
- Unit 3Dokumen21 halamanUnit 3nandan100% (1)
- Machine Learning Project ReportDokumen89 halamanMachine Learning Project ReportKyoto100% (2)
- Syllabus of B.E. Mechanical Engineering ProgrammeDokumen131 halamanSyllabus of B.E. Mechanical Engineering ProgrammegetflybondBelum ada peringkat
- Random Variables and DistributionsDokumen61 halamanRandom Variables and DistributionsRajesh JayachandranBelum ada peringkat
- Gaussian Conjugate Prior Cheat SheetDokumen7 halamanGaussian Conjugate Prior Cheat SheetHirdesh KumarBelum ada peringkat
- Chapter6 ExerciesextraDokumen10 halamanChapter6 ExerciesextranikowawaBelum ada peringkat
- Fraud Detection in Auto InsuranceDokumen28 halamanFraud Detection in Auto InsuranceDinesh ChoudharyBelum ada peringkat
- R AssignmentDokumen8 halamanR AssignmentTunaBelum ada peringkat
- UECM1693/UECM2623/UCCM2623 Tutorial S4: Applications of Statis-TicsDokumen2 halamanUECM1693/UECM2623/UCCM2623 Tutorial S4: Applications of Statis-Ticssadyehclen0% (1)
- Operations Management: An Integrated ApproachDokumen11 halamanOperations Management: An Integrated Approachsam heisenbergBelum ada peringkat
- 10.cluster AnalysisDokumen68 halaman10.cluster AnalysisironchefffBelum ada peringkat
- Do Psychedelics Mimic KundaliniDokumen10 halamanDo Psychedelics Mimic KundaliniGabriel MarquesBelum ada peringkat
- 2017 - OPUS Quant Advanced PDFDokumen205 halaman2017 - OPUS Quant Advanced PDFIngeniero Alfonzo Díaz Guzmán100% (1)
- Internet and Mobile Phone Addiction PDFDokumen330 halamanInternet and Mobile Phone Addiction PDFAnanth PrabhuBelum ada peringkat