CCC
Diunggah oleh
Nipuna Thushara WijesekaraDeskripsi Asli:
Judul Asli
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
CCC
Diunggah oleh
Nipuna Thushara WijesekaraHak Cipta:
Format Tersedia
Chapter
BINOMIAL THEOREM
8.1 Overview:
8.1.1 An expression consisting of two terms, connected by + or sign is called a
binomial expression. For example, x + a, 2x 3y,
1 1
4
, etc., are all binomial
3 , 7x
5y
x x
expressions.
8.1.2 Binomial theorem
If a and b are real numbers and n is a positive integer, then
(a + b)n =nC0 an + nC1 an 1 b1 + nC2 an 2 b2 + ...
... + nCr an r br + ... + nCn bn, where nCr =
8.1.3
1.
2.
3.
4.
n
for 0 r n
r nr
The general term or (r + 1)th term in the expansion is given by
Tr + 1 = nCr anr br
Some important observations
The total number of terms in the binomial expansion of (a + b)n is n + 1, i.e. one
more than the exponent n.
In the expansion, the first term is raised to the power of the binomial and in each
subsequent terms the power of a reduces by one with simultaneous increase in
the power of b by one, till power of b becomes equal to the power of binomial,
i.e., the power of a is n in the first term, (n 1) in the second term and so on
ending with zero in the last term. At the same time power of b is 0 in the first
term, 1 in the second term and 2 in the third term and so on, ending with n in the
last term.
In any term the sum of the indices (exponents) of a and b is equal to n (i.e.,
the power of the binomial).
The coefficients in the expansion follow a certain pattern known as pascals
triangle.
130
EXEMPLAR PROBLEMS MATHEMATICS
Index of Binomial
Coefficient of various terms
0
1
2
3
4
5
1
1
1
1
1
2
3
1
1
3
6
10
1
4
10
1
5
Each coefficient of any row is obtained by adding two coefficients in the preceding
row, one on the immediate left and the other on the immediate right and each row is
bounded by 1 on both sides.
The (r + 1)th term or general term is given by
n
Tr + 1 =
Cr an r br
8.1.4 Some particular cases
If n is a positive integer, then
(a + b)n = nC0 an b0 + nC1 an b1 + nC2 an 2 b2 + ... + nCr an r br + ... +
n
C n a0 b n
In particular
... (1)
1. Replacing b by b in (i), we get
(a b)n = nC0 an b0 nC1 an 1 b1 + nC2 an 2 b2 + ... + (1)r nCr an r br + ... +
(1)n nCn a0 bn
... (2)
2. Adding (1) and (2), we get
(a + b)n + (a b)n = 2 [nC0 an b0 + nC2 an 2 b2 + nC4 an 4 b4 + ... ]
= 2 [terms at odd places]
3. Subtracting (2) from (1), we get
(a + b)n (a b)n = 2 [nC1 an 1 b1 + nC3 an 3 b3 + ... ]
= 2 [sum of terms at even places]
4. Replacing a by 1 and b by x in (1), we get
(1 + x)n =nC0 x0 + nC1 x + nC2 x2 + ... + nCr xr + ... + nCn
n
i.e.
(1 + x)n =
n Cr x r
r =0
xn 1 + nCn xn
BINOMIAL THEOREM
131
5. Replacing a by 1 and b by x in ... (1), we get
(1 x)n = nC0 x0 nC1 x + nC2 x2 ... + nCn1 (1)n1 xn-1 + nCn (1)n xn
n
i.e.,
(1 x)n =
(1)r
r =0
Cr x r
8.1.5 The pth term from the end
The pth term from the end in the expansion of (a + b) n is (n p + 2)th term from the
beginning.
8.1.6 Middle terms
The middle term depends upon the value of n.
(a) If n is even: then the total number of terms in the expansion of (a + b)n is n + 1
th
(odd). Hence, there is only one middle term, i.e., n + 1 term is the middle
2
term.
(b) If n is odd: then the total number of terms in the expansion of (a + b)n is n + 1
n + 1
(even). So there are two middle terms i.e.,
2
middle terms.
th
n + 3
and
2
th
are two
8.1.7 Binomial coefficient
In the Binomial expression, we have
(a + b)n =nC0 an + nC1 an 1 b + nC2 an 2 b2 + ... + nCn bn
... (1)
n
n
n
n
The coefficients C0, C1, C2, ... , Cn are known as binomial or combinatorial
coefficients.
Putting a = b = 1 in (1), we get
n
C0 + nC1 + nC2 + ... + nCn = 2n
Thus the sum of all the binomial coefficients is equal to 2n.
Again, putting a = 1 and b = 1 in (i), we get
n
C0 + nC2 + nC4 + ... = nC1 + nC3 + nC5 + ...
Thus, the sum of all the odd binomial coefficients is equal to the sum of all the even
binomial coefficients and each is equal to
n
2n
= 2 n1 .
2
C0 + nC2 + nC4 + ... = nC1 + nC3 + nC5 + ... = 2n 1
132
EXEMPLAR PROBLEMS MATHEMATICS
8.2 Solved Examples
Short Answer Type
2r
Example 1 Find the r term in the expansion of x + .
x
th
1
Solution We have Tr = 2rCr 1 (x)2r r + 1
x
2r
xr + 1
r 1 r +1
2r
x2
r 1 r +1
r 1
r+1
Example 2 Expand the following (1 x + x2)4
Solution Put 1 x = y. Then
(1 x + x2)4 = (y + x2)4
= 4C0 y4 (x2)0 + 4C1 y3 (x2)1
+ 4C2 y2 (x2)2 + 4C3 y (x2)3 + 4C4 (x2)4
= y4 + 4y3 x2 + 6y2 x4 + 4y x6 + x8
= (1 x)4 + 4x2 (1 x)3 + 6x4 (1 x)2 + 4x6 (1 x) + x8
= 1 4x + 10x2 16x3 + 19x4 16x5 + 10x6 4x7 + x8
x3 2
Example 3 Find the 4th term from the end in the expansion of 2
2 x
Solution Since rth term from the end in the expansion of (a + b)n is (n r + 2)th term
from the beginning. Therefore 4th term from the end is 9 4 + 2, i.e., 7th term from the
beginning, which is given by
3
9
x 3 2 6 9 x 64 9 8 7 64 672
= 3
C
T7 = C6 2 =
3
8 x12 3 2 1 x3
x
2 x
Example 4 Evaluate: x 2 1 x 2
) + (x
4
+ 1 x2
BINOMIAL THEOREM
133
1 x 2 = y , we get
Solution Putting
The given expression = (x2 y)4 + (x2 + y)4 = 2 [x8 + 4C2 x4 y2 + 4C4 y4]
8 4 3 4
x (1 x 2 ) + (1 x 2 ) 2
= 2 x +
2 1
= 2 [x8 + 6x4 (1 x2) + (1 2x2 + x4]
= 2x8 12x6 + 14x4 4x2 + 2
2
Example 5 Find the coefficient of x11 in the expansion of x3
x2
12
Solution Let the general term, i.e., (r + 1)th contain x11.
12
We have
2
2
x
3 12 r
Tr + 1 = Cr (x )
= 12Cr x36 3r 2r (1)r 2r
= 12Cr (1)r 2r x36 5r
Now for this to contain x11, we observe that
36 5r = 11, i.e., r = 5
Thus, the coefficient of x11 is
12
C5 (1)5 25 =
12 11 10 9 8
32 = 25344
5 4 3 2
2
Example 6 Determine whether the expansion of x 2
x
containing x10?
Solution Let Tr + 1 contain x10. Then
Tr + 1 =
18
2 18 r
Cr ( x )
2
x
= 18Cr x36 2r (1)r . 2r x r
= (1)r 2r 18Cr x36 3r
Thus,
36 3r = 10, i.e., r =
26
3
18
will contain a term
134
EXEMPLAR PROBLEMS MATHEMATICS
Since r is a fraction, the given expansion cannot have a term containing x10.
10
x
3
Example 7 Find the term independent of x in the expansion of
+ 2 .
3 2x
Solution Let (r + 1)th term be independent of x which is given by
Tr+1 =
10
x
Cr
3
x
= 10 Cr
3
r
10
Cr 3 2
10 r
10 r
2
3
2
2x
1
32 r 2r
2 x
10 r
2 2 r
10 r
2r
2
Since the term is independent of x, we have
10 r
2r = 0
r= 2
2
Hence 3rd term is independent of x and its value is given by
T3 =
10
C2
33 10 9
1
5
=
=
4
2 1 9 12 12
12
Example 8 Find the middle term in the expansion of 2ax 2 .
x
Solution Since the power of binomial is even, it has one middle term which is the
th
12 + 2
term and it is given by
2
T7 =
12
b
C6 (2ax)6 2
x
12
C6
26 a 6 x 6 (b)6
x12
12
C6
26 a 6b6 59136a 6b6
=
x6
x6
BINOMIAL THEOREM
135
p x
Example 9 Find the middle term (terms) in the expansion of + .
x p
Solution Since the power of binomial is odd. Therefore, we have two middle terms
which are 5th and 6th terms. These are given by
5
p 126 p
p x
T5 = 9 C4 = 9 C4 =
x
x
x p
4
p x 9 x 126 x
T6 = C5 = C5 =
p
p
x p
9
and
Example 10 Show that 24n + 4 15n 16, where n N is divisible by 225.
Solution We have
24n + 4 15n 16 = 24 (n + 1) 15n 16
= 16n + 1 15n 16
= (1 + 15)n + 1 15n 16
= n + 1C0 150 + n + 1C1 151 + n + 1C2 152 + n + 1C3 153
+ ... + n + 1Cn + 1 (15)n + 1 15n 16
= 1 + (n + 1) 15 + n + 1C2 152 + n + 1C3 153
+ ... + n + 1Cn + 1 (15)n + 1 15n 16
= 1 + 15n + 15 + n + 1C2 152 + n + 1C3 153
+ ... + n + 1Cn + 1 (15)n + 1 15n 16
= 152 [n + 1C2 + n + 1C3 15 + ... so on]
Thus, 24n + 4 15n 16 is divisible by 225.
Long Answer Type
Example 11 Find numerically the greatest term in the expansion of (2 + 3x)9, where
x=
3
.
2
3x
Solution We have (2 + 3x) = 2 1 +
2
136
EXEMPLAR PROBLEMS MATHEMATICS
Tr + 1
Now,
Tr
3x
29 9 C r
2
=
r 1
3x
2 9 9 C r 1
2
r 1 10 r 3 x
Cr 3x
9
=
r 9r
9
2
Cr 1 2
Tr + 1
Therefore,
Tr
10 r 3x
10 r 9
=
r 4
r
2
Since
3
2
x=
90 9r
1
4r
90 9r 4r
(Why?)
90
13
r6
12
13
Thus the maximum value of r is 6. Therefore, the greatest term is Tr + 1 = T7.
9 3 x 6
T7 = 2 C6 ,
2
Hence,
where x =
3
2
6
12
7 313
9
9 98 7 3
9 9
2
=
2
C
6 =
3 2 1 212
2
4
Example 12 If n is a positive integer, find the coefficient of x1 in the expansion of
n
(1 + x)n 1 + .
x
Solution We have
(1 + x) 1 +
n
n
(1 + x) 2 n
1
n x + 1
= (1 + x)
=
xn
x
x
BINOMIAL THEOREM
Now to find the coefficient of x in (1 + x) 1 +
coefficient of x1 in
137
1
, it is equivalent to finding
x
(1 + x) 2 n
which in turn is equal to the coefficient of xn 1 in the
xn
expansion of (1 + x)2n.
Since (1 + x)2n = 2nC0 x0 + 2nC1 x1 + 2nC2 x2 + ... + 2nCn 1 xn1 + ... + 2nC2n x2n
Thus the coefficient of xn 1 is 2nCn 1
=
2n
2n
=
n 1 n +1
n 1 2n n + 1
Example 13 Which of the following is larger?
9950 + 10050 or 10150
We have (101)50 = (100 + 1)50
= 10050 + 50 (100)49 +
Similarly
50.49
50.49.48
(100) 47 + ... (1)
(100)48 +
2.1
3.2.1
9950 = (100 1)50
= 10050 50 . 10049 +
50.49
50.49.48
(100) 47 + ... (2)
(100)48
2.1
3.2.1
Subtracting (2) from (1), we get
49
10150 9950 = 2 50 (100) +
50 49 48
10047 + ...
3 2 1
50 49 48
10047 + ...
3 2 1
10150 9950 = 10050 + 2
10150 9950 > 10050
Hence 10150 >9950 + 10050
Example 14 Find the coefficient of x50 after simplifying and collecting the like terms
in the expansion of (1 + x)1000 + x (1 + x)999 + x2 (1 + x)998 + ... + x1000.
Solution Since the above series is a geometric series with the common ratio
its sum is
x
,
1+ x
138
EXEMPLAR PROBLEMS MATHEMATICS
x 1001
(1 + x)
1
1 + x
x
1 1 + x
1000
x 1 001
1+ x
= (1 + x)1001 x1001
1+ x x
1+ x
(1 + x )1 00 0
=
Hence, coefficient of x50 is given by
1001
C 50 =
1001
50 951
Example 15 If a1, a2, a3 and a4 are the coefficient of any four consecutive terms in
the expansion of (1 + x)n, prove that
a3
a1
2a2
+
=
a1 + a2 a3 + a4 a2 + a3
Solution Let a1, a2, a3 and a4 be the coefficient of four consecutive terms Tr + 1, Tr +
, Tr + 3, and Tr + 4 respectively. Then
2
a1 = coefficient of Tr + 1 = nCr
a2 = coefficient of Tr + 2 = nCr + 1
a3 = coefficient of Tr + 3 = nCr + 2
and
a4 = coefficient of Tr + 4 = nCr + 3
Thus
a1
=
a1 + a2
Cr
Cr + n Cr + 1
n
n +1
Cr
Cr + 1
(Q
Cr + nCr + 1 = n + 1Cr + 1 )
BINOMIAL THEOREM
Similarly,
139
r + 1 n r r + 1
n
=
n +1
r nr
n + 1
n
Cr + 2
a3
= n
a3 + a4
Cr + 2 + nCr + 3
n
Cr + 2
n +1
Cr + 3
r+3
n +1
Hence,
L.H.S. =
a3
a1
r + 1 r + 3 2r + 4
+
=
+
=
a1 + a2 a3 + a4 n + 1 n + 1 n + 1
and
R.H.S. =
2 n Cr + 1
2 n Cr + 1
2a2
=
= n +1
a2 + a3 n Cr + 1 + n Cr + 2
Cr + 2
= 2
r + 2 n r 1 2 (r + 2)
n
=
r +1 n r 1
n +1
n +1
Objective Type Questions (M.C.Q)
Example 16 The total number of terms in the expansion of (x + a)51 (x a)51 after
simplification is
(a) 102
(b) 25
(c) 26
(d) None of these
Solution C is the correct choice since the total number of terms are 52 of which 26
terms get cancelled.
Example 17 If the coefficients of x and x in 2 +
x
are equal, then n is
3
(a) 56
(b) 55
(c) 45
(d) 15
n
nr r
Solution B is the correct choice. Since Tr + 1 = Cr a x in expansion of (a + x)n,
Therefore,
T8 = C7 (2)
n7
2n 7 7
x
n
=
C
x
7
3
37
7
140
EXEMPLAR PROBLEMS MATHEMATICS
n 8
x n 2
8
= C8 8 x
3
3
8
and
T9 =
Therefore,
C8 (2)
n8
2n 7
2n 8
n
C7 7 = C8 8 (since it is given that coefficient of x7 = coefficient x8)
3
3
8 n 8 2n 8 37
n
=
7 n7
n
38 2n 7
8
1
=
n7 6
n = 55
Example 18 If (1 x + x2)n = a0 + a1 x + a2 x2 + ... + a2n x2n, then a0 + a2 + a4 + ...
+ a2n equals.
(A)
3n + 1
2
(B)
3n 1
2
(C)
1 3n
2
Solution A is the correct choice. Putting x = 1 and 1 in
(1 x + x2)n = a0 + a1 x + a2 x2 + ... + a2n x2n
we get
1 = a0 + a1 + a2 + a3 + ... + a2n
and
3n = a0 a1 + a2 a3 + ... + a2n
n
(D) 3 +
1
2
... (1)
...
(2)
Adding (1) and (2), we get
3n + 1 = 2 (a0 + a2 + a4 + ... + a2n)
Therefore a0 + a2 + a4 + ... + a2n =
3n + 1
2
Example 19 The coefficient of xp and xq (p and q are positive integers) in the
expansion of (1 + x)p + q are
(A) equal
(B) equal with opposite signs
(C) reciprocal of each other
(D) none of these
Solution A is the correct choice. Coefficient of xp and xq in the expansion of (1 + x)p
+q
are p + qCp and p + qCq
p+q
and
p+q
Cp = p + qCq =
Hence (a) is the correct answer.
p q
BINOMIAL THEOREM
141
Example 20 The number of terms in the expansion of (a + b + c)n, where n N is
(A)
( n + 1) ( n + 2)
2
(B) n + 1
(C) n + 2
(D) (n + 1) n
Solution A is the correct choice. We have
(a + b + c)n = [a + (b + c)]n
= an + nC1 an 1 (b + c)1 + nC2 an 2 (b + c)2
+ ... + nCn (b + c)n
Further, expanding each term of R.H.S., we note that
First term consist of 1 term.
Second term on simplification gives 2 terms.
Third term on expansion gives 3 terms.
Similarly, fourth term on expansion gives 4 terms and so on.
The total number of terms = 1 + 2 + 3 + ... + (n + 1)
=
(n + 1) (n + 2)
2
Example 21 The ratio of the coefficient of x15 to the term independent of x in
2
x +
15
(A) 12:32
is
(B) 1:32
(C) 32:12
(D) 32:1
15
Solution (B) is the correct choice. Let Tr + 1 be the general term of x 2 + , so,
x
15
2 15 r
Tr + 1 = Cr (x )
2
x
= 15Cr (2)r x30 3r
Now, for the coefficient of term containing x15,
30 3r = 15, i.e., r = 5
15
5
Therefore, C5 (2) is the coefficient of x15 (from (1))
To find the term independent of x, put 30 3r = 0
... (1)
142
EXEMPLAR PROBLEMS MATHEMATICS
Thus 15C10 210 is the term independent of x (from (1))
15
C 5 25
1
1
= 5=
Now the ratio is 15
10
32
C10 2
2
5
3 i
3 i
Example 22 If z =
+ +
, then
2
2
2
2
(A) Re (z) = 0
(B) Im (z) = 0
(C) Re (z) > 0, Im (z) > 0
(D) Re (z) > 0, Im (z) < 0
Solution B is the correct choice. On simplification, we get
2
3
3
3 i 2 5 3
5
5
+ C2 + C4
z = 2 C0
2
2 2
2
4
i
2
Since i2 = 1 and i4 = 1, z will not contain any i and hence Im (z) = 0.
8.3 EXERCISE
Short Answer Type
15
3x 2 1
.
1. Find the term independent of x, x 0, in the expansion of
3x
2
k
2. If the term free from x in the expansion of x 2
10
is 405, find the value
of k.
3. Find the coefficient of x in the expansion of (1 3x + 7x2) (1 x)16.
4. Find the term independent of x in the expansion of, 3x
5. Find the middle term (terms) in the expansion of
x a
(i)
a x
10
x3
(ii) 3x
15
2
.
x2
BINOMIAL THEOREM
143
6. Find the coefficient of x15 in the expansion of (x x2)10.
7. Find the coefficient of
1
in the expansion of
x17
15
4 1 .
x 3
x
1 n
8. Find the sixth term of the expansion y 2 + x 3
, if the binomial coefficient of
the third term from the end is 45.
[Hint: Binomial coefficient of third term from the end = Binomial coefficient of
third term from beginning = nC2.]
9. Find the value of r, if the coefficients of (2r + 4)th and (r 2)th terms in the
expansion of (1 + x)18 are equal.
10. If the coefficient of second, third and fourth terms in the expansion of (1 + x)2n
are in A.P. Show that 2n2 9n + 7 = 0.
11. Find the coefficient of x4 in the expansion of (1 + x + x2 + x3)11.
Long Answer Type
8
12. If p is a real number and if the middle term in the expansion of + 2 is
2
1120, find p.
13. Show that the middle term in the expansion of x
2n
is
1 3 5 ... (2n 1)
( 2) n .
n
n
1
3
14. Find n in the binomial 2 + 3 if the ratio of 7th term from the beginning to
3
the 7th term from the end is
1
.
6
15. In the expansion of (x + a)n if the sum of odd terms is denoted by O and the sum of
144
EXEMPLAR PROBLEMS MATHEMATICS
even term by E.
Then prove that
(i) O2 E2 = (x2 a2)n
(ii) 4OE = (x + a)2n (x a)2n
2
16. If x occurs in the expansion of x +
2n
, prove that its coefficient is
2n
.
4n p 2n + p
3
3
1
3
17. Find the term independent of x in the expansion of (1 + x + 2x ) x 2 .
2
3x
3
Objective Type Questions
Choose the correct answer from the given options in each of the Exercises 18 to 24
(M.C.Q.).
18. The total number of terms in the expansion of (x + a)100 + (x a)100 after
simplification is
(A) 50
(B) 202
(C) 51
(D) none of these
th
19. Given the integers r > 1, n > 2, and coefficients of (3r) and (r + 2)nd terms in
the binomial expansion of (1 + x)2n are equal, then
(A) n = 2r
(B) n = 3r
(C) n = 2r + 1
(D) none of these
20. The two successive terms in the expansion of (1 + x)24 whose coefficients are in
the ratio 1:4 are
(A) 3rd and 4th (B) 4th and 5th
(C) 5th and 6th
(D) 6th and 7th
Cr
1
r +1 1
=
= 4r + 4 = 24 4 r = 4 ]
24 r 4
Cr + 1 4
24
[Hint:
24
21. The coefficient of xn in the expansion of (1 + x)2n and (1 + x)2n 1 are in the ratio.
(A) 1 : 2
(B) 1 : 3
(C) 3 : 1
(D) 2 : 1
2n
2n 1
[Hint : Cn :
Cn
22. If the coefficients of 2nd, 3rd and the 4th terms in the expansion of (1 + x)n are in
A.P., then value of n is
(A) 2
(B) 7
(c) 11
(D) 14
n
n
n
2
[Hint: 2 C2 = C1 + C3 n 9n + 14 = 0 n = 2 or 7
BINOMIAL THEOREM
145
23. If A and B are coefficient of xn in the expansions of (1 + x)2n and (1 + x)2n 1
A
equals
B
respectively, then
(A) 1
(B) 2
2n
A
=
[Hint:
B
(C)
(D)
1
n
Cn
= 2]
Cn
2n 1
24. If the middle term of + x sin x
x
(A) 2n +
1
2
10
(B) n +
6
6
is equal to 7
7
, then value of x is
8
(C) n + (1)n
(D) n + (1)n
3
6
1
1
1 5
63
5
sin5 x = 5 sin =
x
sin
x
=
2
2
8
x5
x = n + (1)n ]
6
[Hint: T6 =
10
C5
Fill in the blanks in Exercises 25 to 33.
25. The largest coefficient in the expansion of (1 + x)30 is _________________ .
26. The number of terms in the expansion of (x + y + z)n _________________ .
[Hint: (x + y + z)n = [x + (y + z)]n]
16
27. In the expansion of x 2
1
, the value of constant term is
x2
_________________ .
28. If the seventh terms from the beginning and the end in the expansion of
n
1
3
2 + 3 are equal, then n equals _________________ .
3
[Hint : T7 = T n 7 + 2
C ( )
6
1 n6
23
1
1
3
3
( ) 1
1 6
C n 6 2 3
=
3
3
n6
146
EXEMPLAR PROBLEMS MATHEMATICS
( )
1 n 12
23
1
= 1
33
n 12
only problem when n 12 = 0 n = 12].
1 2b
a 3
29. The coefficient of a 6 b4 in the expansion of
[Hint : T5 =
10
10
is _________.
1120 6 4
1 2b
C4
=
a b ]
a 3
27
30. Middle term in the expansion of (a3 + ba)28 is _________ .
31. The ratio of the coefficients of xp and xq in the expansion of (1 + x)p + q is_________
[Hint: p + qCp = p + qCq]
x
3
+ 2
32. The position of the term independent of x in the expansion of
3 2x
10
is
_________ .
33. If 2515 is divided by 13, the reminder is _________ .
State which of the statement in Exercises 34 to 40 is True or False.
10
34.
20
The sum of the series C r
r= 0
19
is 2 +
20
C10
2
35. The expression 79 + 97 is divisible by 64.
Hint: 79 + 97 = (1 + 8)7 (1 8)9
36. The number of terms in the expansion of [(2x + y3)4]7 is 8
37. The sum of coefficients of the two middle terms in the expansion of (1 + x)2n 1
is equal to 2n 1Cn.
38. The last two digits of the numbers 3400 are 01.
39. If the expansion of x 2
2n
contains a term independent of x, then n is a
multiple of 2.
40. Number of terms in the expansion of (a + b)n where n N is one less than the
power n.
Anda mungkin juga menyukai
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDari EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifePenilaian: 4 dari 5 bintang4/5 (5794)
- Shoe Dog: A Memoir by the Creator of NikeDari EverandShoe Dog: A Memoir by the Creator of NikePenilaian: 4.5 dari 5 bintang4.5/5 (537)
- Grade 5 Volume and Capacity/Length and Distance: L ML of PaintDokumen3 halamanGrade 5 Volume and Capacity/Length and Distance: L ML of PaintNipuna Thushara WijesekaraBelum ada peringkat
- Master of Energy Management (Mem) : DMX9402 Thermal Energy Utilities Academic Year 2020 Assignment 1Dokumen1 halamanMaster of Energy Management (Mem) : DMX9402 Thermal Energy Utilities Academic Year 2020 Assignment 1Nipuna Thushara WijesekaraBelum ada peringkat
- Application Form Assist MGR Engineering 22 01 2020Dokumen1 halamanApplication Form Assist MGR Engineering 22 01 2020Nipuna Thushara WijesekaraBelum ada peringkat
- DMX9404 Assignment 1 - 520253279Dokumen18 halamanDMX9404 Assignment 1 - 520253279Nipuna Thushara WijesekaraBelum ada peringkat
- Inverter For IMD - ROI CalculationDokumen1 halamanInverter For IMD - ROI CalculationNipuna Thushara WijesekaraBelum ada peringkat
- Master of Energy Management (Mem) : DMX9405 Renewable Energy Technology Academic Year 2020 Assignment 1Dokumen1 halamanMaster of Energy Management (Mem) : DMX9405 Renewable Energy Technology Academic Year 2020 Assignment 1Nipuna Thushara WijesekaraBelum ada peringkat
- English HP 2016Dokumen18 halamanEnglish HP 2016Nipuna Thushara WijesekaraBelum ada peringkat
- IMD MachineDokumen1 halamanIMD MachineNipuna Thushara WijesekaraBelum ada peringkat
- Abx Aby Ab X Y: Ax by BX Ay Ax BX Ay byDokumen7 halamanAbx Aby Ab X Y: Ax by BX Ay Ax BX Ay byNipuna Thushara WijesekaraBelum ada peringkat
- Abx Aby Ab X Y: Ax by BX Ay Ax BX Ay byDokumen1 halamanAbx Aby Ab X Y: Ax by BX Ay Ax BX Ay byNipuna Thushara WijesekaraBelum ada peringkat
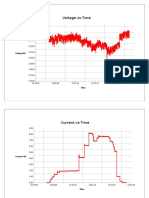
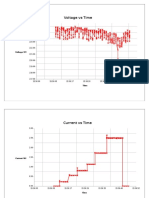
- Voltage Vs TimeDokumen6 halamanVoltage Vs TimeNipuna Thushara WijesekaraBelum ada peringkat
- Field Instruments That Are Connected To Mark VDokumen1 halamanField Instruments That Are Connected To Mark VNipuna Thushara WijesekaraBelum ada peringkat
- 1 Wages Boards OrdinanceDokumen37 halaman1 Wages Boards Ordinancesandhwani3893Belum ada peringkat
- Justifying The Need For Change in Paypal NipunaDokumen3 halamanJustifying The Need For Change in Paypal NipunaNipuna Thushara WijesekaraBelum ada peringkat
- Algebra: Combined Mathematics Revision 2017Dokumen1 halamanAlgebra: Combined Mathematics Revision 2017Nipuna Thushara WijesekaraBelum ada peringkat
- Ict PaperDokumen2 halamanIct PaperNipuna Thushara WijesekaraBelum ada peringkat
- ConclusionsDokumen1 halamanConclusionsNipuna Thushara WijesekaraBelum ada peringkat
- 2nd Term Test Paper-ICT - KS4Dokumen3 halaman2nd Term Test Paper-ICT - KS4Nipuna Thushara Wijesekara100% (1)
- Installation AssingmentDokumen11 halamanInstallation AssingmentNipuna Thushara WijesekaraBelum ada peringkat
- Innovation and Thinking Out of The Box Could Set Hallmark in Any VentureDokumen7 halamanInnovation and Thinking Out of The Box Could Set Hallmark in Any VentureNipuna Thushara WijesekaraBelum ada peringkat
- Small BusinessDokumen7 halamanSmall BusinessNipuna Thushara WijesekaraBelum ada peringkat
- 1 Wages Boards OrdinanceDokumen37 halaman1 Wages Boards Ordinancesandhwani3893Belum ada peringkat
- 2 The Acidic EnvironmentDokumen27 halaman2 The Acidic EnvironmentNipuna Thushara WijesekaraBelum ada peringkat
- Good Data SheetDokumen20 halamanGood Data SheetNipuna Thushara WijesekaraBelum ada peringkat
- Light BulbsDokumen3 halamanLight BulbsNipuna Thushara WijesekaraBelum ada peringkat
- Simulink Model of An Incandescent BulbDokumen3 halamanSimulink Model of An Incandescent BulbNipuna Thushara WijesekaraBelum ada peringkat
- FYP Budget Approval RequestDokumen1 halamanFYP Budget Approval RequestNipuna Thushara WijesekaraBelum ada peringkat
- ReadmeDokumen4 halamanReadmeNipuna Thushara WijesekaraBelum ada peringkat
- The Yellow House: A Memoir (2019 National Book Award Winner)Dari EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Penilaian: 4 dari 5 bintang4/5 (98)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDari EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RacePenilaian: 4 dari 5 bintang4/5 (895)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDari EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersPenilaian: 4.5 dari 5 bintang4.5/5 (344)
- The Little Book of Hygge: Danish Secrets to Happy LivingDari EverandThe Little Book of Hygge: Danish Secrets to Happy LivingPenilaian: 3.5 dari 5 bintang3.5/5 (399)
- Grit: The Power of Passion and PerseveranceDari EverandGrit: The Power of Passion and PerseverancePenilaian: 4 dari 5 bintang4/5 (588)
- The Emperor of All Maladies: A Biography of CancerDari EverandThe Emperor of All Maladies: A Biography of CancerPenilaian: 4.5 dari 5 bintang4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDari EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaPenilaian: 4.5 dari 5 bintang4.5/5 (266)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDari EverandNever Split the Difference: Negotiating As If Your Life Depended On ItPenilaian: 4.5 dari 5 bintang4.5/5 (838)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDari EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryPenilaian: 3.5 dari 5 bintang3.5/5 (231)
- On Fire: The (Burning) Case for a Green New DealDari EverandOn Fire: The (Burning) Case for a Green New DealPenilaian: 4 dari 5 bintang4/5 (73)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDari EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FuturePenilaian: 4.5 dari 5 bintang4.5/5 (474)
- Team of Rivals: The Political Genius of Abraham LincolnDari EverandTeam of Rivals: The Political Genius of Abraham LincolnPenilaian: 4.5 dari 5 bintang4.5/5 (234)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDari EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyPenilaian: 3.5 dari 5 bintang3.5/5 (2259)
- Rise of ISIS: A Threat We Can't IgnoreDari EverandRise of ISIS: A Threat We Can't IgnorePenilaian: 3.5 dari 5 bintang3.5/5 (137)
- The Unwinding: An Inner History of the New AmericaDari EverandThe Unwinding: An Inner History of the New AmericaPenilaian: 4 dari 5 bintang4/5 (45)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDari EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You ArePenilaian: 4 dari 5 bintang4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Dari EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Penilaian: 4.5 dari 5 bintang4.5/5 (120)
- Her Body and Other Parties: StoriesDari EverandHer Body and Other Parties: StoriesPenilaian: 4 dari 5 bintang4/5 (821)
- Calculus 1 - 4. Polynomial Curves (C)Dokumen2 halamanCalculus 1 - 4. Polynomial Curves (C)retchie cambaBelum ada peringkat
- Class 12 Math NotesDokumen4 halamanClass 12 Math NotesChitiyaBelum ada peringkat
- Direct MethodsDokumen46 halamanDirect MethodsZambuk TeaBelum ada peringkat
- Fun With Fourier SeriesDokumen84 halamanFun With Fourier SeriesJuanBelum ada peringkat
- Little Flower School: GorakhpurDokumen4 halamanLittle Flower School: GorakhpurMritunjayBelum ada peringkat
- ch10 PDFDokumen36 halamanch10 PDFcathyBelum ada peringkat
- Trigonometric IdentitiesDokumen1 halamanTrigonometric IdentitiesEye ShieldBelum ada peringkat
- Systems of Equations On The TI-83: Gauss-Jordan Method: Matrix 1Dokumen4 halamanSystems of Equations On The TI-83: Gauss-Jordan Method: Matrix 1madanesherBelum ada peringkat
- Concrete Mathematics Exercises From 20 September: Exercise 1.2Dokumen4 halamanConcrete Mathematics Exercises From 20 September: Exercise 1.2rohanBelum ada peringkat
- Constant: PositiveDokumen3 halamanConstant: PositiveJames Reech SantiagoBelum ada peringkat
- Chapter 4 Power SeriesDokumen55 halamanChapter 4 Power SeriesThalagawali RajagopalBelum ada peringkat
- Unit 5 (Trigonometric Identities)Dokumen34 halamanUnit 5 (Trigonometric Identities)Shaira Mae CajandabBelum ada peringkat
- Linear Equations in 2 VariablesDokumen18 halamanLinear Equations in 2 Variablesat4machineBelum ada peringkat
- Linear PdeDokumen23 halamanLinear PdeA SinghBelum ada peringkat
- Pre-Calculus 11 Textbook CH 4Dokumen65 halamanPre-Calculus 11 Textbook CH 4iamparam31Belum ada peringkat
- SIM Quadratic Equation by SquareDokumen40 halamanSIM Quadratic Equation by SquareRochelle AdlaoBelum ada peringkat
- Thess-DLP-COT Q1-Rational FunctionsDokumen5 halamanThess-DLP-COT Q1-Rational FunctionsThess Valeroso100% (1)
- GMAT Club Guide To OG 2019 v6Dokumen116 halamanGMAT Club Guide To OG 2019 v6AmitiPoddarBelum ada peringkat
- Algebra 2 End of Course Test Preparation WorkbookDokumen7 halamanAlgebra 2 End of Course Test Preparation Workbookafiwjkfpc100% (2)
- Workbook Unit 4 1º ESODokumen30 halamanWorkbook Unit 4 1º ESOFrancisco Botella JuanBelum ada peringkat
- Generating-Sequences 1Dokumen35 halamanGenerating-Sequences 1Paul Andrew GonzalesBelum ada peringkat
- Group LessonsDokumen5 halamanGroup Lessonsapi-394725139Belum ada peringkat
- NP Bali Unit 1Dokumen87 halamanNP Bali Unit 1Aman Pratap SinghBelum ada peringkat
- New Century Math Yr 9 - Chapter03 Products and FactorsDokumen37 halamanNew Century Math Yr 9 - Chapter03 Products and FactorsPung Kang QinBelum ada peringkat
- 2nd Quarter Exam MATH 7Dokumen3 halaman2nd Quarter Exam MATH 7NIDA DACUTANANBelum ada peringkat
- Solving Trig EquationsDokumen12 halamanSolving Trig Equationsapi-285179261Belum ada peringkat
- (University Lecture Series) Hiraku Nakajima - Lectures On Hilbert Schemes of Points On Surfaces-AMS (1999)Dokumen121 halaman(University Lecture Series) Hiraku Nakajima - Lectures On Hilbert Schemes of Points On Surfaces-AMS (1999)kaluzakleinBelum ada peringkat
- Previous Year Sample Paper 3Dokumen23 halamanPrevious Year Sample Paper 3Rajesh K SinghBelum ada peringkat
- BC0052-Theory of Computer ScienceDokumen227 halamanBC0052-Theory of Computer SciencedatatronBelum ada peringkat
- (Maa 1.7) Deductive ProofDokumen10 halaman(Maa 1.7) Deductive ProofAleya NajihaBelum ada peringkat