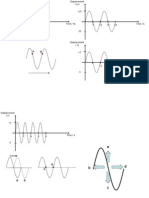
AVG and RMS Values of Periodic Waveforms 2012
Diunggah oleh
Ang Yu LongHak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
AVG and RMS Values of Periodic Waveforms 2012
Diunggah oleh
Ang Yu LongHak Cipta:
Format Tersedia
Average and RMS Values of a Periodic Waveform:
(Nofziger, 2008)
Begin by defining the average value of any time-varying function over a time interval
t t 2 t1 as the integral of the function over this time interval, divided by t :
t2
f avg
f (t ) dt
t1
1 2
=
f (t ) dt
t 2 t1 t1
(1.1)
Numerically, this is an extension of the basic definition of the average for a discrete
N
variable, x
x
i =1
, applied to a continuously-varying function.
Graphically, this means that the area under the function (between times t1 and t 2 ) is
equivalent to the area of a rectangle of height f avg multiplied by width (t 2 t1 ) :
t2
f avg (t 2 t1 ) = f (t ) dt
(1.2)
t1
The average of a sine wave over one half-cycle:
Consider a sine wave of peak amplitude Ip and frequency f:
I (t ) = I p sin (2f t ) = I p sin (t )
The period of the wave, , is given as:
1 2
=
f
The average value of one half-cycle in time, is then calculated as:
2
2I p 2
1
sin (t )dt
I avg =
I sin (t )dt =
( 2) 0 p
0
2 I p cos(t ) 2 2 I p
cos
=
I avg =
|
2
2I p
4I p 4I p
1 =
=
cos ( ) +=
=
2
I=
avg
2I p
=
(.637 ) I p
(1.3)
(1.4)
(1.5)
() cos(0)
2I p
calculated over one half-cycle of the sine wave
(1.6)
(1.7)
The average of a sine wave over one full-cycle:
I avg =
( ) 0
I p sin (t )dt
(1.8)
I p cos(t ) I p
I avg =
|0 = [ cos( ) () cos(0)]
Ip
I
[ cos(2 ) + 1] = p [ 1 + 1] = 0
=
I avg = 0
calculated over one full-cycle of the sine wave
(1.9)
While this result is mathematically correct, it doesnt provide any physical insight into
what this sine wave can accomplish over one complete cycle. Consider the AC
sinusoidal voltage delivered by Tucson Electric Power at a wall outlet. Its average value
may be 0, yet we know from experience that this sine wave will light up fluorescent
bulbs, heat up tungsten filaments in light bulbs, heat wires in toasters, etc. This is
because these devices absorb energy (power) from the sine wave, whether the voltage is
positive-going or negative-going. Useful work is done during both half-cycles of the
sinusoidal waveform.
The problem, mathematically, is that we have added up negative as well as positive
values. To account for this and make sure that all parts of the waveform contribute to its
calculated effective value, first square the function f (t ) so that all values are positive.
Then add up (integrate) all values of f (t ) over one complete cycle, and finally take the
square root. This is known as the Root Mean Square or RMS value of any timevarying (or spatially-varying) waveform, and is defined as:
YRMS
{f
(t )
AVG
(t )dt
(1.10)
The physical meaning of the RMS value is thisit is the constant, or DC value that
would cause the same physical effect as the actual time-varying waveform does, during
one complete period. This might be to deliver the same power in a circuit, to cause the
same heating effect in a toaster, to light up a bulb with the same brightness, etc.
Note that, in general, a periodic waveform may not have symmetry like sinusoidal or
triangular waveforms have. In this case, you still calculate the RMS value according to
equation (1.10), by integrating over one complete cycle. Modern-day instrumentation
(the DMMs and oscilloscopes in our lab) digitally sample a waveform, and numerically
integrate the values to calculate the RMS value, according to equation (1.10).
RMS Value of a Sinusoidal Waveform:
Consider a sinusoidal voltage of peak amplitude V p and frequency f:
V (t ) = V p sin (2f t ) = V p sin (t )
The RMS value is calculated as:
VRMS =
2
V (t )dt =
0
2
p
sin 2 (t )dt
(1.12)
V p
1
(
)
1
cos
2
t
dt
dt
cos(
2
t
)
dt
0
0 2
2 0
Vp
2
V p sin( 2t )
=
(t )
2 0 2 0
VRMS
=
Vp
=
2
(.707 )Vp
(1.13)
(1.14)
V p sin( 2 )
V p sin( 2 2 )
0 =
0
=
2 2
2
2
Vp
(1.11)
[ 0 + 0] =
Vp
(1.15)
for a sinusoidal waveform
(1.16)
(1.17)
(Note that you get the same result whether you integrate from (0 ) , (0 2) , or even
from (0 4) , because of the symmetry of this waveform. For non-symmetrical
waveforms, you have to integrate over the complete cycle.)
The quoted value of 120VAC for the voltage at the wall socket, as delivered by Tucson
Electric Power is, in fact, the RMS value of the (60Hz) sinusoidal voltage. The peak
voltage is therefore V p = 2 120 = 169 V, and the peak-to-peak value is 339V!!!
RMS Value of a Triangular Waveform:
Consider a triangular voltage waveform that is bi-polar, has a 50% duty-cycle
(symmetrical about V=0), and a frequency f. Let the maximum voltage be Vp, and the
minimum voltage be Vp.
Because of the symmetry, integrate from (0 4) to calculate the RMS value:
V (t ) =
4V p
(valid between t = 0 and t = 4 )
(1.18)
VRMS = V
AVG
1
=
V 2 (t )dt
4 0 0
(1.19)
4
4
4 4V p 2
4 4V p
t dt =
t 2 dt
=
0
0
2
2
64V p t 3
=
3 3
VRMS
=
Vp
=
3
(.577 )Vp
2
2
Vp
64V p 3
=
=
3
3 3 4 3
for a triangular waveform
(1.20)
(1.21)
(1.22)
RMS Value of a Rectangular Waveform:
Consider a rectangular voltage waveform that is bi-polar, has a 50% duty-cycle
(symmetrical about V=0), and a frequency f. Let the maximum voltage be Vp, and the
minimum voltage be Vp.
Because of the symmetry, integrate from (0 2) to calculate the RMS value:
(valid between t = 0 and t = 2 )
V (t ) = V p
=
VRMS
=
V 2 AVG
2
=
VRMS = V p
2
2
=
(Vp ) dt
1
2
2
(t )dt
V=
2
2
=
(Vp ) t 0 2
for a rectangular waveform
(V ) dt
2
(1.23)
(1.24)
(V ) (
2 0)
(1.25)
(1.26)
Anda mungkin juga menyukai
- Open-Circuit or No-Load TestDokumen13 halamanOpen-Circuit or No-Load TestNANDHAKUMAR ABelum ada peringkat
- Interpret AC Voltages & CurrentsDokumen46 halamanInterpret AC Voltages & CurrentsKelvin LooiBelum ada peringkat
- Generation Of Alternating Emf: E = EmsinөDokumen9 halamanGeneration Of Alternating Emf: E = EmsinөjojojojoBelum ada peringkat
- Garcia College AC 1 Phase Problem GuideDokumen15 halamanGarcia College AC 1 Phase Problem GuideZen GarciaBelum ada peringkat
- Experiment No.3Dokumen6 halamanExperiment No.3justinepunzalan250% (1)
- Example 2PES2015Dokumen3 halamanExample 2PES2015FaizahmedBelum ada peringkat
- Chapter 3 Energy of A System ThermoDokumen25 halamanChapter 3 Energy of A System ThermoEmadudin AbdulkaderBelum ada peringkat
- AC Quantities ExplainedDokumen7 halamanAC Quantities Explainedsrinivas100% (1)
- Zener Diode and Diode ApplicationDokumen62 halamanZener Diode and Diode Applicationnibar dyllanBelum ada peringkat
- Ac Single Phase First PartDokumen32 halamanAc Single Phase First PartreyiBelum ada peringkat
- Chapter21 TransformerDokumen25 halamanChapter21 TransformerChin Chee FeeBelum ada peringkat
- AC Circuits Fundamentals QuizDokumen4 halamanAC Circuits Fundamentals QuizCris Diane G. DatingginooBelum ada peringkat
- TransformerDokumen29 halamanTransformergolu100% (1)
- The Equations of The Currents in Two Parallel Connected Electric Devices Are I1Dokumen3 halamanThe Equations of The Currents in Two Parallel Connected Electric Devices Are I1Tim Picar100% (1)
- Transformer 1 2Dokumen94 halamanTransformer 1 2Tobi AQWBelum ada peringkat
- AparatusDokumen187 halamanAparatusNorman Jay GarciaBelum ada peringkat
- Plates in EnerconDokumen38 halamanPlates in EnerconJevan Calaque100% (1)
- ELE 2117 Lesson 6Dokumen49 halamanELE 2117 Lesson 6elioBelum ada peringkat
- Interpretation of Data and Result and Conclusion. Exp.6 - Resonance FrequencyDokumen1 halamanInterpretation of Data and Result and Conclusion. Exp.6 - Resonance FrequencydummyBelum ada peringkat
- Auto TransformerDokumen5 halamanAuto TransformerAugy HaerudyBelum ada peringkat
- DC-DC ConvertersDokumen30 halamanDC-DC ConvertersTema HassanBelum ada peringkat
- PART IV. Instrument TransformersDokumen30 halamanPART IV. Instrument TransformersuplbselesBelum ada peringkat
- Transformer Dot NotationDokumen3 halamanTransformer Dot NotationsunilsathishBelum ada peringkat
- Cap 5Dokumen29 halamanCap 5deberes ucacueBelum ada peringkat
- Tutorial 1 - Basic Concepts in Power ElectronicsDokumen7 halamanTutorial 1 - Basic Concepts in Power ElectronicsJohn Appleseed100% (1)
- 3 Phase Ac Problems With SolutionDokumen12 halaman3 Phase Ac Problems With SolutionKim FetalverBelum ada peringkat
- Bipolar Junction Transistor: E B CE CBDokumen18 halamanBipolar Junction Transistor: E B CE CBMohammadAshraful100% (1)
- Proposed 15 Numerical Problems For PresentationDokumen8 halamanProposed 15 Numerical Problems For PresentationalexBelum ada peringkat
- 1 (1) 4Dokumen10 halaman1 (1) 4Angga SeptianBelum ada peringkat
- PTDU Lab No. 10 Study of Real Time Operation of Bus Bars Abdul Wahab Nasir (02) Bsee 16-20Dokumen2 halamanPTDU Lab No. 10 Study of Real Time Operation of Bus Bars Abdul Wahab Nasir (02) Bsee 16-20Ali ArshadBelum ada peringkat
- Understanding Multiphase CircuitsDokumen15 halamanUnderstanding Multiphase CircuitsNidhija PillayBelum ada peringkat
- Lec # 021 Thermal Time ConstantDokumen16 halamanLec # 021 Thermal Time ConstantAyeshaBelum ada peringkat
- CH-2-DC MachineDokumen83 halamanCH-2-DC MachineÙm ØrthøbøyBelum ada peringkat
- AE LAB - Experiment No.2-1Dokumen4 halamanAE LAB - Experiment No.2-1Prajwal PatilBelum ada peringkat
- AC Circuits 1 Batch 13Dokumen2 halamanAC Circuits 1 Batch 13Jan Henry JebulanBelum ada peringkat
- Module 2 Alternator TestsDokumen20 halamanModule 2 Alternator TestsJoshua Roberto GrutaBelum ada peringkat
- As Water and Their Application in Engineering.: HydraulicsDokumen8 halamanAs Water and Their Application in Engineering.: HydraulicsrenegadeBelum ada peringkat
- AC Circuit Analysis Using PhasorsDokumen22 halamanAC Circuit Analysis Using PhasorsvsabioniBelum ada peringkat
- Circuits 3 ProblemDokumen5 halamanCircuits 3 ProblemraramalazaBelum ada peringkat
- CH2Dokumen55 halamanCH2Shantha KumarBelum ada peringkat
- Fundamentals of Electrical Engineering Chapter ThreeDokumen24 halamanFundamentals of Electrical Engineering Chapter Threetemesgen adugnaBelum ada peringkat
- DistributionsDokumen4 halamanDistributionsReparrBelum ada peringkat
- Circuit Lab MPMS 2018-2019 Science Olympiad TestDokumen6 halamanCircuit Lab MPMS 2018-2019 Science Olympiad TestMadhavi VangipurapuBelum ada peringkat
- Communication Engineering Cycle Test 1 AnDokumen2 halamanCommunication Engineering Cycle Test 1 AnsamBelum ada peringkat
- Solution of Tutorial Sheet-3 (Three Phase Networks) : Ans. Given, - Vab - 45kV, ZL (0.5 + j3), Z (4.5 + j9)Dokumen10 halamanSolution of Tutorial Sheet-3 (Three Phase Networks) : Ans. Given, - Vab - 45kV, ZL (0.5 + j3), Z (4.5 + j9)Shroyon100% (2)
- EEL2026-LabsheetDokumen23 halamanEEL2026-LabsheetchandraBelum ada peringkat
- Sect2-3 PDFDokumen10 halamanSect2-3 PDFBlaiseBelum ada peringkat
- MCQ of DC Machines Madhuri NewDokumen31 halamanMCQ of DC Machines Madhuri NewAnkit KumarBelum ada peringkat
- EE GATE 2000 Question and AnswersDokumen8 halamanEE GATE 2000 Question and AnswersUTKAL.45Belum ada peringkat
- Objective QuestionsUNIT - 3&4Dokumen17 halamanObjective QuestionsUNIT - 3&4Omkar Shete50% (2)
- Experiment V Current Control of An SCR I. ObjectiveDokumen4 halamanExperiment V Current Control of An SCR I. ObjectiveDenisse Torizo Olan100% (1)
- Transformers to Convert Three-Phase Power to Two-Phase Power RatingsDokumen1 halamanTransformers to Convert Three-Phase Power to Two-Phase Power RatingsToper GarciaBelum ada peringkat
- Pitch Factor N Distribution FactorDokumen5 halamanPitch Factor N Distribution FactorKim KeatBelum ada peringkat
- Experiment No. 1: AIM: To Observe Sine Wave, Square Wave, Triangular Wave and RampDokumen2 halamanExperiment No. 1: AIM: To Observe Sine Wave, Square Wave, Triangular Wave and RampAnand SinghBelum ada peringkat
- HW4 SolutionsDokumen10 halamanHW4 SolutionsBrooklyn Luqii100% (1)
- Average and RMS Values of A Periodic Waveform:: T T T T DT T F FDokumen4 halamanAverage and RMS Values of A Periodic Waveform:: T T T T DT T F Fdhar_sauravBelum ada peringkat
- Single-Phase AC Circuits: Version 2 EE IIT, KharagpurDokumen13 halamanSingle-Phase AC Circuits: Version 2 EE IIT, KharagpurSai SrivatsaBelum ada peringkat
- ECE212 Circuit Analysis Lecture ObjectivesDokumen6 halamanECE212 Circuit Analysis Lecture ObjectivesFrew FrewBelum ada peringkat
- Lecture 4Dokumen17 halamanLecture 4Mouath AlsebaieBelum ada peringkat
- Topic 1 Sinusoids and Phasors - Week 7Dokumen77 halamanTopic 1 Sinusoids and Phasors - Week 7Adnan HazimehBelum ada peringkat
- Uncertainty and MeasurementsDokumen2 halamanUncertainty and MeasurementsAng Yu LongBelum ada peringkat
- Thermal Properties of Matter HWDokumen2 halamanThermal Properties of Matter HWAng Yu LongBelum ada peringkat
- YJC Physics NotesDokumen725 halamanYJC Physics NotesAng Yu LongBelum ada peringkat
- Booklet-Profiting With Futures Options PDFDokumen44 halamanBooklet-Profiting With Futures Options PDFAng Yu LongBelum ada peringkat
- IB Wave Properties Practice QuestionsDokumen2 halamanIB Wave Properties Practice QuestionsAng Yu LongBelum ada peringkat
- Study of Short Term Reversion Techniques in TradingDokumen14 halamanStudy of Short Term Reversion Techniques in TradingAng Yu LongBelum ada peringkat
- DOCUMENT - Concise summary of key ideasDokumen12 halamanDOCUMENT - Concise summary of key ideasAng Yu LongBelum ada peringkat
- Gas Laws Homework ExplainedDokumen2 halamanGas Laws Homework ExplainedAng Yu LongBelum ada peringkat
- Mathematics PicturesDokumen8 halamanMathematics PicturesAng Yu LongBelum ada peringkat
- Vegas 4 Hour Tunnel MethodDokumen13 halamanVegas 4 Hour Tunnel MethodGreg VermeychukBelum ada peringkat
- Using The Fisher TransformDokumen6 halamanUsing The Fisher Transformchristianp3Belum ada peringkat
- Share Market Analyss - 250819 PDFDokumen51 halamanShare Market Analyss - 250819 PDFArijit BhattacharyaBelum ada peringkat
- Gravitational FieldDokumen30 halamanGravitational FieldAng Yu LongBelum ada peringkat
- 8 RMS PDFDokumen4 halaman8 RMS PDFraymund12345Belum ada peringkat
- Projectile Motion PracticeDokumen4 halamanProjectile Motion PracticeAng Yu LongBelum ada peringkat
- Assessment Task 1 Test Projectile and Circular MotionDokumen5 halamanAssessment Task 1 Test Projectile and Circular MotionAng Yu LongBelum ada peringkat
- Predictability of Nonlinear Trading Rules in The US MarketDokumen41 halamanPredictability of Nonlinear Trading Rules in The US MarketAng Yu LongBelum ada peringkat
- Particles and Accelerators PracticeDokumen4 halamanParticles and Accelerators PracticeAng Yu LongBelum ada peringkat
- Standing Waves and Resonance - PracticeDokumen2 halamanStanding Waves and Resonance - PracticeAng Yu LongBelum ada peringkat
- Physics Formulae and Data Sheet Stage 3 2015Dokumen4 halamanPhysics Formulae and Data Sheet Stage 3 2015Ang Yu LongBelum ada peringkat
- Physics PicturesDokumen6 halamanPhysics PicturesAng Yu LongBelum ada peringkat
- WACE Physics Stage 2 Formulae and Constants SheetDokumen8 halamanWACE Physics Stage 2 Formulae and Constants SheetAng Yu LongBelum ada peringkat
- Electrical Components ForDokumen6 halamanElectrical Components ForAng Yu LongBelum ada peringkat
- TFT LCD Specification for 3.5Dokumen36 halamanTFT LCD Specification for 3.5kumaraswamyhollavBelum ada peringkat
- Installation Guide: 2.4 Inch TFT Terminal Time Attendance & Access ControlDokumen13 halamanInstallation Guide: 2.4 Inch TFT Terminal Time Attendance & Access ControlDatashield InfoBelum ada peringkat
- Battery Less PhoneDokumen7 halamanBattery Less PhoneNaveen Gowdru Channappa50% (2)
- Diagrama Fonte DeltaDokumen7 halamanDiagrama Fonte DeltacesarBelum ada peringkat
- Cri-1000 2Dokumen5 halamanCri-1000 2Zeeshan AhmadBelum ada peringkat
- Diesel Generator Ratings and SpecificationsDokumen4 halamanDiesel Generator Ratings and SpecificationsoscarBelum ada peringkat
- RSS - Empaque - X450 ADokumen2 halamanRSS - Empaque - X450 AAlejandroBelum ada peringkat
- 8051 BasicsDokumen22 halaman8051 BasicsviswapraveenBelum ada peringkat
- Reverse Engineering Power Management On NVIDIADokumen9 halamanReverse Engineering Power Management On NVIDIALeofodãoBelum ada peringkat
- PI Controlled Bi-Directional DC-DC Converter (BDDDC) and Highly Efficient Boost Converter For Electric VehiclesDokumen5 halamanPI Controlled Bi-Directional DC-DC Converter (BDDDC) and Highly Efficient Boost Converter For Electric VehiclesOscar Olarte OrtizBelum ada peringkat
- High Power PA Amplifiers: SSA-250MDokumen1 halamanHigh Power PA Amplifiers: SSA-250MsenthilSK0% (1)
- Lecture Notes Week 1 Introduction To MicroprocessorDokumen51 halamanLecture Notes Week 1 Introduction To Microprocessormargetrie100% (1)
- Cadence Design Tools TutorialDokumen124 halamanCadence Design Tools TutorialBhupender KumawatBelum ada peringkat
- Paper Presentation On Mobile Computing 1Dokumen5 halamanPaper Presentation On Mobile Computing 1arulbenjaminchandru67% (3)
- Irjet V7i3986Dokumen5 halamanIrjet V7i3986Vasu ThakurBelum ada peringkat
- Basics of Analog and Digital CommunicationDokumen19 halamanBasics of Analog and Digital CommunicationinduBelum ada peringkat
- A Practical Introduction To Hardwaresoftware Codesign 1Dokumen64 halamanA Practical Introduction To Hardwaresoftware Codesign 1s_subbulakshmiBelum ada peringkat
- Wall Mounted G4 Series High Performance and Powerful Air Ow: DC InverterDokumen2 halamanWall Mounted G4 Series High Performance and Powerful Air Ow: DC InverterZacke EsmaBelum ada peringkat
- 60 Cell: LG320N1C-G4 I LG315N1C-G4 LG310N1C-G4 I LG305N1C-G4Dokumen2 halaman60 Cell: LG320N1C-G4 I LG315N1C-G4 LG310N1C-G4 I LG305N1C-G4Jesus David Muñoz RoblesBelum ada peringkat
- Raycap CatalogueDokumen26 halamanRaycap CatalogueMagesh VenuBelum ada peringkat
- ToshibaDokumen175 halamanToshibajuse192002Belum ada peringkat
- Brkewn 3014Dokumen84 halamanBrkewn 3014vssreekanth_321Belum ada peringkat
- Man BNWAS 2.0.1 EngDokumen38 halamanMan BNWAS 2.0.1 Eng'Egemen KayaBelum ada peringkat
- 4007ES Fire Control PanelsDokumen8 halaman4007ES Fire Control PanelsJorge Renato Chirinos QuiñonezBelum ada peringkat
- Substation Filter BankSpecsDokumen7 halamanSubstation Filter BankSpecsTudor BostanBelum ada peringkat
- Strategy for Undervoltage Load Shedding Using Dynamic Load ModelingDokumen5 halamanStrategy for Undervoltage Load Shedding Using Dynamic Load ModelingSyaifuddinZuhriBelum ada peringkat
- The Hill Chart of A Francis Turbine Is Indicated in The Figure. The Turbine Is Operating With A HeadDokumen4 halamanThe Hill Chart of A Francis Turbine Is Indicated in The Figure. The Turbine Is Operating With A HeadBorja PumaresBelum ada peringkat
- Step Response Unit ResponseDokumen6 halamanStep Response Unit ResponsetirsollantadaBelum ada peringkat
- Huawei FM1000A40 V200R003C00 IT Maintenance GuideDokumen179 halamanHuawei FM1000A40 V200R003C00 IT Maintenance GuideJesusBelum ada peringkat
- NIC Components NSP SeriesDokumen6 halamanNIC Components NSP SeriesNICCompBelum ada peringkat