Project Details: Page # 1 of

Ribbed Slab Designs to BS 8110-97: Prepared: Y.A

Continuous 6m Long Spans & Imposed Loading 2.5kPa Checked:
REF CALCULATIONS OUTPUT
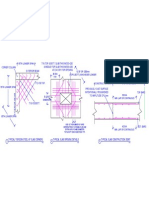
Slab Geometry:
6m 6m 6m

- Design a one-way ribbed slab with 3 equal continuous spans

BS8110- - It satisfies the criteria of BS8110 for using Table 3.12
3.5.2.3 &
3.5.2.4 For +ve moment, design the most critical section:
i.e. End Span, Span (upport c-r) L= 6 m
For -ve moment, design the most critical section:
i.e. First Interior Support
Material Properties:
fy = 460 N/mm (main & shear reinforcement)
fcu = 30 N/mm (C25/30 Concrete)
RCC Weight = 25 kN/m

Loading:
Floor Finishes & Services (SDL) = 1.20 kN/m2
Rapidwall Formwork (SDL) = 0.4 kN/m2
BS6399-1 Characteristic Imposed Load = 2.50 kN/m2

Slab Sizing:
Let topping thickness, hf = 100 mm
Rib width, bw = 230 mm
Flange Width b = 500 mm (Rib spacing)
bw/b = 0.46 > 0.3
BS8110- Interpolating Basic L/d = 26 -4.01 = 22.0
3.4.6.3
Table 3.9 Let modification factor = 1.6 (to be confirmed later)
Allowable L/d ratio = 35.2
Therefore, dmin= 170.5 mm

Bottom cover to links = 25 mm (includes 5mm for

deviation)

Rapidwall bottom skin = 15 mm

Dia of main bars = 14 mm
Dia of links = 8 mm
hreq = 225.5 mm
Try an overall depth of slab h = 224 mm
 Project Details: Page # 2 of
Ribbed Slab Designs to BS 8110-97: Prepared: Y.A
Continuous 6m Long Spans & Imposed Loading 2.5kPa Checked:
REF CALCULATIONS OUTPUT
Ulitmate Load & Moment Calculation:
Width of slab carried by one rib = 500 mm
Self-weight of slab = 1.88 kN/m
Design Dead Load = 1.4xDL = 3.75 kN/m
Design Implosed Load = 1.6xLL = 2.00 kN/m
Total Design Load, w = 5.75 kN/m
Total Design Load on a span, F = wL = 34.48 kN

BS8110- Ultimate bending moment and shear force as per Table 3.12
3.5.2.3 & 0.086FL
3.5.2.4 0.063FL

BMD

0.086FL 0.063FL

0.5F 0.5F
0.4F

0.5F SFD
0.6F

Design of End Span (Bottom Reinforcement):

Ultimate Moment M = 0.086 FL = 17.8 kNm

T section, b = 500 mm, d = 169 mm

Assume 0.9x = hf = 100 mm
Mf = 0.45 fcu b hf (d - 0.5hf) = 80.325 kNm >M
Neutral axis lies in the flange; treat as a rectangular section,
having width b = 500 mm, h = 224 mm

BS8110- K = M/(fcu b d2) = 0.042 < 0.156

3.4.4.4
hence compression reinforcement is not required
z/d = 0.5+(0.25 - K/0.9) = 0.95 0.95
z = 0.95d = 160.55
Provide Bottom
As req = M/(0.87 fy z) = 277 mm2 Reinforcement
BS8110- Minimum reinforcement check: web in tension, bw/b0.4 2Y 14
Table 3.25
BS8110-
Table 3.25
Asmin = 0.13% bw h = 67 mm2 1Y 14
Asprov(mm )= 462
2

Project Details: Page # 3 of

Ribbed Slab Designs to BS 8110-97: Prepared: Y.A
Continuous 6m Long Spans & Imposed Loading 2.5kPa Checked:
REF CALCULATIONS OUTPUT
Design of First Interior Support (Top Reinforcement):

Ultimate Moment M = 0.086 FL = 17.8 kNm

Hogging moment over support; slab bottom face in compression.

Ribs are not terminated before the support, hence:
Solid section: b = 230 mm, h = 224 mm

BS8110- Table coefficient include 20% redistribution of moment at support

3.5.2.3 &
3.5.2.4 b = 0.8
K' = 0.402(bb 0.4) 0.18(bb 0.4)2 = 0.132

BS8110- K = M/(fcu b d2) = 0.051 < K'

3.4.4.4
hence compression reinforcement is not required
z/d = 0.5+(0.25 - K/0.9) = 0.94 0.95
z = 0.95d = 160.55
Provide Top
As req = M/(0.87 fy z) = 277 mm2 Reinforcement
BS8110- Minimum reinforcement check: for rectangular sections 2Y 10
Table 3.25
3.12.11.2 Asmin = 0.13% b h = 67 mm2 +1Y 12
Asprov(mm2)= 270
Shear Check:
Max. shear force at first interior support = 0.6F = 20.7 kN
Ribs are not terminated before the support, hence critical section is at
the face of the load-bearing Rapidwall:

x= 62 mm from support centerline

Shear Force V = (0.6F) - (wx) = 20.3 kN
BS8110- Calculate design applied shear stress:
Eq. 22
v = V/bvd = 0.52 N/mm < vcmax= 4.38
BS8110- Calculate design concrete shear stress:
Table 3.8
100 As/bvd = 0.70 3
(400/d)1/4 = 1.24 0.67
BS8110- vc = (0.79/gm)*{100As/(bwd)} 1/3
(400/d) 1/4
(fcu/25) = 0.74 N/mm v < vc , no shear
3.6.4.7 links required
BS8110- v < vc , no shear
3.6.4.7 links required
BS8110- 'Where two or more bars are used in a rib, the use of link reinforcement
3.6.6.3 is recommended to ensure correct cover to reinforcement. The spacing of Provide Double
the links can generally be of the order of 1 m to 1.5 m depending on the Legged Links
size of the main bars'
Y8@500mm c/c

Project Details: Page # 4 of

Ribbed Slab Designs to BS 8110-97: Prepared: Y.A
Continuous 6m Long Spans & Imposed Loading 2.5kPa Checked:
REF CALCULATIONS OUTPUT
Deflection Check (Middle of End Span):
BS8110- Code says that Table 3.9 ratios "are based on limiting the total deflection to
3.4.6.3 span/250 and this should normally ensure that the part of the deflection
Table 3.9 occurring after construction of finishes and partitions will be limited to
span/500 or 20 mm, whichever is the lesser, for spans up to 10 m"

bw/b = 0.46 > 0.3,

Interpolated Basic L/d = 22.0
M/bd2 = 1.25 N/mm
b 0.95
BS8110- fs = 194 N/mm
Eq. 8

BS8110-
Eq. 7

tension m.f = 1.65 2 = 1.65

As'prov = 157 mm As'prov/bd = 0.19

compression m.f = 1.06 1.5 = 1.06
Allowable L/d = Basic L/d*m.f = 38.4
Actual L/d = 35.5 < Allowable L/d Deflection Check
No further checks are required. Satisfactory
Reinforcement in Topping:
Single layer of welded steel fabric is needed for the topping:
Use Mesh A252
BS8110- Taking 1m width of the topping, b = 1000 mm Y8 bars
3.6.6.2
As = 0.12% b hf = 120 mm2/m S = 200 mm
Maximum spacing Smax = rib spacing/2 = 250 mm As = 252 mm2/m
Detailing Diagram: