GB iiverroo. PHYS370 — Advanced Electromagnetism Part 9: Electromagnetism and Special Relativity Review of Special Relativity Special relativity is developed from two fundamental principles: ‘* Physical laws have the same form in all inertial frames of reference. ‘All observers find the same value, c in a vacuum, for the speed of light ‘pavanced Elecromagretiom 1 Pant 9 EM and Special Rest Lorentz Transformations Lorentz Transformations Consider two inertial frames $ and S$" (i.e, two non-accelerating reference frames). Suppose that the two frames have a common origin (x = y= z= 0) at time = 0, and that the coordinates are oriented so that the relative velocity of the frames is parallel to the x axis. Frame $ Prame $” y yf A given event occurs at time ¢ and coordinates (z,y,2) in frame S, and at time t! and coordinates (2!,¥/,2") in frame S'. The relationship between the times ¢ and l’, and the coordinates (9.2) and (@/,y',2!) is given by a Lorentz transformation For a given event, the time and coordinates of the event in the frame S! are found from 1e time and coordinates of the even in the frame $ using a Lorentz transformation: 2 = e-v) a voy @) vas @) ¢ = 9(-3) @) where: (5) and v is the relative speed of S’ with respect to S. ‘Advanced Eleevromagretism 2 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 3 Part 9: EM and Special RelatityThe Inverse Lorentz Transformations Time Dilation The “inverse” transformation gives the time and coordinates of an event in S, in terms of the time and coordinates of the same The Lorentz transformations have two immediate consquences. The first is that the time interval tg ~ ¢ between two events in frame S is greater than the time interval t ~ t, between the same two events, occuring at a given point 2! in frame S (6) (7) Since: (8) : he o(a r ay (9) ’ where, 28 before 2 = 7(¢+4) aa) ao) 1 felons that te — tr = r(ty- th) (13) Note that +> 1 for all vi therefor, “moving clocks run slow" Length Contraction The second immediate consequence of the Lorentz, transformation is that the distance xb ~ 24, between in frame 5" is less than the distance 2 ~ 1 between the same ‘two events, occuring at a given time # in frame S. so events Since: A = (-) (aa) 2 = y(22- 08) as) it follows that: (as) The dimension along the x axis of an object moving parallel to the x axis appears to be shorter than if the same measurement was made on the same object at rest. ‘Advanced Eleevromagretism 6 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 7 Part 9: EM and Special RelatityLorentz Invariance A physical quantity that is unchanged under the Lorentz transformation is said to be Lorentz invariant. For example consider a pulse of light that leaves the origin at time t=" =0, and propagates as a spherical wave. An observer at rest in S describes the locus of the spherical wavefront at time ¢ by the equation PtyPt2= PF = P4y?+2-2P%=0 (17) But, from the fundamental principles of special relativity, an observer at rest in S! sees the light pulse travel at the same speed c, $0 writes a similar equation for the locus of the spherical wavefront in S' 244 2 24 a? ty? $2? 2? =0 a) The quantity 2? + y? + 2? — 21? has the same value (zero) for all inertial observers: it is said to be Lorentz invariant. ‘aavanced Liecvomagretsm 8 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism ° Part 9 EM and Special Relat Electric Charges Seen by Different Observers Flectric charge does not depend on time or position: therefore, the net charge carried by an object is Lorentz invariant. However, from Maxwell's equations, an electric feld is generated by a charge density, p v-B=p as) The charge density is the charge per unit volume. Since the volume of an object is not Lorentz invariant (because of Lorentz contraction), charge density is not Lorentz invariant. This suggests that electric (and magnetic) fields are not Lorentz invariant. Observers in different inertial frames will agree on how an electromagnetic system behaves, but will give different explanations for its behaviour. We can illustrate this with a simple example. 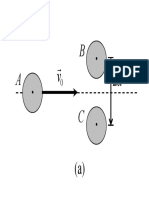‘Aavanced Eleevromagretism 10 Part 9: EM and Special Relatty Electromagnetic Forces Seen by Different Observers Consider a long straight wire at rest in a frame S with zero net charge, but carrying a current 1 A charge q moving in the same direction as the current in the wire feels a magnetic force pushing it towards the wire v, ‘Aavanced Elecromaoretism n Part 9: EM and Special RelatityElectromagnetic Forces Seen by Different Observers An observer in S sees an electrically neutral wire, with the same number of negative and positi /e charges per unit length. Let us suppose that the current arises from positive charges moving with speed v in the same direction as the charge ¢. Since the wire is electrically neutral, the charge line densities of e stationary negative charges and the moving positive charges are the same. Electromagnetic Forces Seen by Different Observers At a radial distance r from the wire, the observer in $ sees a magnetic field! vol pate 2. oar (20) The charge g moving at speed w parallel to the wire at a distance r from the wire experiences a force: Hol ar where the minus sign indicates a force towards the wire for positive q, v and 1. F = qh =a a Using Newton's second law of motion, the acceleration of the charge resulting from the magnetic force is: @r_ oF Cr FL 22) Wm Fm" Oar (22) where m is the mass of the charge in its rest frame. ‘aevanced Gicvomagretam 12 Pans €w and Space Rely ‘nsvancod Eecvomagnetiom 13 Panto EM and Speci Romy Electromagnetic Forces Seen by Different Observers Now consider an observer in S’, the rest frame of the charge g. This observer should also see the charge accelerate towards the wire, Using time dilation, dt = ydt'; so the rate of acceleration in s* should be: @r adr Pr per 4 bol 5 (23) we tn One But In S’, the charge is at rest: this means that it will feel no force from the magnetic field around the wire So why does the charge accelerate in S'? Electromagnetic Forces Seen by Different Observers Consider the wire as viewed by the observer in S' ‘Suppose there are N charged particles per unit length of the wire when viewed in S. The number of negative charges per unit length when viewed in S! is yN (since the negative charges were at rest in S, and are moving with speed v in S") The number of positive charges per unit length when viewed in S'is N/y (ince the positive charges were moving with speed v in S, and are stationary when viewed in 5") ‘Advanced Eleevromagretism 4 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 15 Part 9: EM and Special RelatityElectromagnetic Forces Seen by Different Observers Electromagnetic Forces Seen by Different Observers The densities of the negative and positive charges do not cancel in S': the net charge line density 9’ is: x = we(2-a) om-3) (24) Since the current J comes from positive charges ¢ with charge density Ne per unit length moving with speed v, we can write: 5) Hence the charge line density is y (28) evened Cecvomsaretsm 16 Pats EM and pec Remy arced Bearonsaneiam 77 Par EM and Soe Rey Electromagnetic Forces Seen by Different Observers Electromagnetic Forces Seen by Different Observers Distances perpendicular to the direction of motion are not , “The electrostatic force on the wire in Ss: affected by relativistic contraction, 50 the charge q is at the same distance r from the wire in the frame $" as in the frame 5 (29) The electric field at the position of the charge is Hence, the acceleration of the charge in St is 1 - or ee Treg c en wr Ft Hol (20) a2 im m nr Si (2 Qe i writter Using 1/ Hosa, this can be written: This is in agreement with equation (23) — even though we @) derived the result in a completely different way. ‘evans Eecvomosvelsm 1 po: Ew ard Spec Ret ‘need Eecronosneion 19 Pai: Ew and Spec ReiElectromagnetic Forces Seen by Different Observers The force on the particle which was purely magnetic in § appears purely electrostatic in 5’ Observers in the two frames agree about the acceleration, but disagree about the origin of the force causing the acceleration. Electric ané magnetic fields are “interchangeable”: whether fone sees an electric or a magnetic field in a given situation depends on one’s frame of reference. This example represents a special case of the transformation of electric and magnetic fields in special relativity. In what follows, we will first show that Maxwell's equations are compatible with special relativity, then derive the general form of the field transformations. ‘Aavanced Eleivomagretism 20 Par 9 EM and Special Relatay Four-Vectors and the Geometry of Space-Time The Lorentz transformation is a linear transformation connecting space and time coordinates in one frame with those in another frame. Can we devise a more natural notation that treats space (z,y,2) and time ¢ coordinates on an equal footing? The answer is Yes! We simply extend the concept of a three-dimensional vector: (yz) @y to four dimensions; thus we write a four-vector: (eyzet) (32) Note that we write ct for the fourth component of a four-vector, so that it has the same units (i.e, units of length) as the other three components. Three-vectors obey certain rules of geometry. We need to be careful about how we extend these rules to four-vectors. ‘Advanced Ee:tomagnetism 2 Part 9: EM and Specai Reatty Three-Vectors and Rotations The length (or rather, the length squared) of a three-vector is found by taking the scalar product: Three-Vectors and Rotations We can write the rotation about the z axis as a matrix Parra tyt? (33) Foot = RO) 7 (7) where The quantity +? is invariant under rotations of the axes. For . cosé sing 0 , 2 0 0 1 = sl =xcosotysing (3a) yo y=-zsind +ycose (35) zo dae (36) ‘aavanced Eleeromoaretim 2 Port 9: EM and Special Reaty ‘aevanced Electromagnetiom 2 Part 9: EM and Special ReatyThree-Vectors and Rotations Three-Vectors and Rotations We observe that the rotation matrices are orthonormal, i.e Rd)" - RY) = Ts (39) where Ig is the 3 x 3 identity matrix. Another way of saying this, is that the rotation matrices preserve the identity matrix, Le. R(G)T Ig RY) = Is (40) This is true for rotations around the « axis and around the y axis, as well as rotations around the z axis. Note that the scalar product of two three-vectors can be written as a matrix multiplication (41) Under a rotation R, we have FORE (42) and the length of the vector is transformed Riis RF (43) But since the rotation matrix R preserves the identity matrix: Par? RT -Ig-R=13 (44) the length of the vector ¥'is invariant under R: Tops. fa? (48) ‘Aavanced Eleivomagretism 2 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism 25 Part 9 EM and Special Relat Four-Vectors and the Geometry of Space-Time Four-Vectors and the Geom y of Space-Time The square of the length of a three-vector r? is invariant under rotations. To extend this concept quantity: four-vectors, we recall that the We note that, like the identity matrix Js in three dimensions, the m 1x q is invariant under rotations. Pasty te? 2? (48) For example if we write the rotation about the = axis as: is invariant under Lorentz transformations. cose sing 0 0 =sing cosé 0 0 R() Oo 18 (49) Let us write this as: 0 0 01 r oF 7) then we have where is now a four-vector, and g is a four-by-four matrix: Rd)" +9 RCS) (50) z 1000 y 0100 =|" t=l003 0 (48) a 000-1 ‘avanced Biectromagretim 36 Part: EM and Speci Realy ‘havanced Becvomagectom ra Part: EM and Speci ReaiyFour-Vectors and the Geometry of Space-Time The fourth dimension gives us an extra set of transformations under which the matrix g is invariant. The minus sign on the (4,4) component of g means that these transformations look a little different from normal ‘transformations. Four-Vectors and the Geometry of Space-Time Let us write: y= cosho (52) where @ Is the parameter in one of the transformations A(2) Using the identity: cosh? 9 ~ sinh?9 = (53) ‘An example of one of these transformations is: we can write: cosh@ 0 0 ~sinne sinho = By (4) a@=f 2 19 0 (1) 0 01 0 where sinh@ 0 9 cosho (ss) ‘Aavanced Eleivomagretism 28 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism 29 Part 9: EM and Specai Reatty Four-Vectors and the Geometry of Space-Time Four-Vectors and the Geom y of Space-Time Summary: By combining the spatial coordinates and the time coordinate into a single four-vector: Then the transformation A(@) becomes: = + 00 —By ¥ (ss) Ao) oon (55) io By 00 7 and considering transformations A(@) that leave the matrix 9 , invariant With @ = of formation A(0) the Lorent 3383 ith d= v/e, the transformation A(0) gives the Lorentz , jlo transformation (1) (4): ACT -9-AMO=9 9=19 59 8 wa) 000-1 Ao) S7 co en we have obtained the Lorentz transformations: yy 00 ay w@=| 2 29 2], y=cosne, py=sino by OO ¥ (woFour-Vectors and the Geometry of Space-Time Four-Vectors and Index Notation A Lorentz boost is just a kind of “rotation” in space-time. The matrix g, sometimes called the metric, is invariant under normal rotations (in three-dimensional space) and under Lorentz boost “rotations” in space-time The metric provides a rule for constructing invariant quantities, We have already seen that for i= (2,y,2,¢t) describing the motion of a spherical wavefront of a light wave, the quantity: P+yPt2-PP=0 (61) is invariant under Lorentz transformations. In general, if # and 7 are four-vectors, then the quantity: The product of two four vectors Food (63) appears all the time in special relativity. To simplify things, we write the pth component (= 1...4) of a four-vector fas pi Note that jis written as a superscriot, We define a four-vector associated with # with components: P= Yo Pave (64) The components of the new four-vector are distinguished from those of the original four-vector by writing the index x as a subscript. The square of the “length” of the four-vector 7 is given by: Pood (62) ‘ is invariant under Lorentz transformations. This is because the Fog B= Yo pop = D> pe (65) metric g is preserved under Lorentz transformations. wren “ ‘Aavanced Eleivomagretism 32 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism 33 Part 9: EM and Specai Reatty Four-Vectors, Index Notation and the Summation Convention Four-Vectors, Index Notation and the Summation Convention In general, the “scalar product” of two four-vectors can be written as 4 ‘ 9 = Sp avnat = SS pus (6s) woe ist A product of two four-vectors constructed in this way is Lorentz invariant. Products such as these occur so frequently in special relativity, ‘at we introduce a short-hand notation that avoids writing the summation symbol all the time. ‘The summation convention states: where a “down” index on ‘one four-vector also appears as an “up” index on another four-vector, we sum over the components of the two four-vectors, thus: Put = Spe = 3) pr avuat (67) =A pe In general, any index should appear a maximum of two times in any expression: once as a “down” index and once as an “up” index When an index appears twice in this way, summation over the index is implied. If an index appears twice or more as either a “down” index or an “up" index, you are doing something wrong! Stop, go back, and check what you have wri ‘Advanced Eleevromagretism 34 Part 9: EM and Special Relatty ‘Aavanced Elecromagretism 35 Part 9: EM and Special RelatityLorentz Transformations of Four-Vectors The Momentum Four-Vector ‘The transformation of a four-vector pH from one inertial frame S into a second intertial frame s’ can be written very easily as: p= Np” (6a) where the summation convention applies, and the matrix AM, has components (in the case of a boost along the = axis): y 00 ~by H, o 10 0 a, 0 010 (69) By oo ¥ Note that to maintain consistency with the summation convention, the matrix A’, is written with one index “up” and the other index "down" A four-vector can be constructed from the energy of a particle and its momentum. If the energy (the sum of the mass energy and the kinetic energy) of a particle is and its momentum is P,Py ps), then the vector py be Py bh (70) £ is a four-vector, called the momentum four-vector of the particle. The “length” squared of the momentum four-vector is given by: 2424p 2 22 Purl = wh + vf +2 — Ty = — be mm where mo is the rest mass of the particle. ‘Aavanced Eleivomagretism 36 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism 37 Part 9 EM and Special Relat The Momentum Four-Vector The Differential Operator a We can re-write this as: BP = 2 + Bet (72) Which is familiar from special relativity. Since all observers agree on the rest mass of a particle, the rest mass is Lorentz invariant, So the quantity pup" is Lorentz invaria four-vector. hence, p# must be a The differential oper: r BH is a four-vector whose components ae ae = (73) se gS To see that 0!" is indeed a four-vector, we must check its transformation rules. ‘Advanced Eleevromagretism 38 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 39 Part 9: EM and Special RelatityThe Differential Operator a The Differential Operator a, and the D’Alembertian The first component transforms as: a at a Associated with aH is the differential operator 6. 2 2 oa an ba) Bt (ray 1 fa Using the inverse Lorentz transformation (6) - (9) for a boost Bn = 0d! (Z (80) in the + direction: (7s) We detine the differential operator 9 as 1= ao" (a1) Altogether, we find the components 4 transform as: Note that we use the summation convention, so that a a = yal —pyat @ summation over the repeated index mis implied P= (77) = Ga) From the components of the vectors, we can write: a Bye +704 (79) 2 1a 22 (2) Hence, a! transforms the same way as 2! under a Lorentz sransformation, and is therefore a four-vector. Aevareed Ercromsgretsm 0 Part: Ew and Spec Remiviy ‘Raareed Uecronsancion i Parte: wane Spec Remi The Differential Operator oH, and the D’Alembertian 1) The Current Density Four-Vector The current density (Jz, Jy, Jz) and the charge density p can be The second-order differential operator [. combined into a four-vector: ae a, a a a J! = (Je, Jy, Jeep)" 84 ee a (3) ¢ ”) (84) a tagtaz Za” ar is called the D'Alembertian. Since the D’Alembertian is the product of two four-vectors, we expect it to be Lorentz invariant. This is indeed the case, as can be verified by calculating its transformation properties directly. The correct transformation properties for a four-vector follow from the Lorentz invariance of electric charge, together with time dilation and length contraction We 494 Me Pay Tyme 8) (zero) which is obviously Lorentz invariant. yd! = ‘Advanced Eleevromagretism 42 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 43 Part 9: EM and Special RelatityCovariant Form The Electromagnetic Potential Four-Vector ‘An equation expressed purely in terms of four-vectors and Lorentz invariants is said to be in covariant form If an equation can be put into covariant form, it means that the equation will still have the same form (i.e. will look the same) if all the quantities involved undergo a Lorentz transformation An equation that is in covariant form will be consistent with e first principle of special relativity. We expect to be able to express the laws of physics (in so far as they are compatible with special relativity) in covariant form. Consider the wave equations for the magnetic vector ang electric scalar potential i = pol (86) be = -2 (87) = Write the second equation as at = 285 = -Hovo (es) We can combine equations (86) and (88) as follows: DAY = —poJ* (89) where J! = (Je, Jy, Jz,¢p)" is the curre and we have defined the quantity AM as: density four-vector, @ AM = (As, Ay, Ass) (90) ‘Aavanced Eleivomagretism aa Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism a Part 9 EM and Special Relat The Electromagnetic Potential Four-Vector A Moving Point Charge: The Liénard-Wiechert Potentials ‘The operator (I is Lorentz invariant, as is the physical constant Mo, and the current density J# is a four-vector, We assume that AM is a four-vector, called the electromagnetic potential four-vector, Then, the wave equation (89): DAK = —po J! Involves only Lorentz invariants and four-vectors, and hence is In covariant form. We can apply a Lorentz transformation to the potentials around a stationary point charge to find the potentials around 2 point charge moving at a constant velocity. The resulting potentials are known as the Liénard-Wiechert potentials We start with the familiar Coulomb potential around a stationary point charge q 14 93 The Lorenz gauge condition: °O = Ta (3) (91) A@ = 0 (94) can be written in covariant forts where Fy isthe location of the point charge aA =0 (2) We now make a Lorentz transformation from a frame in which the point charge is at rest. to one in which itis moving with some non-zero velocityA Moving Point Charge: The Lignard-Wiechert Potentials Let us choose a coordinate system in which the charge is at rest, and the charge and the observation point lie on the z-axis. We shall first consider a boost along the z-axis, and then generalise our result to include boosts in other directions. In the inertial frame S, the point charge is at rest. In the inertial frame S', the charge is moving with velocity » along the 2’-axis Therefore, frame S! is moving with velocity —v along the z-axis with respect to frame 5. ‘A Moving Point Charge: The Liénard-Wiechert Potentials The Lorentz transformations of the potentials are then: # = ¥b+rAD) = 706 (95) Ay = 9(Ae4 3) = (96) Since the vector potential Al, is readily expressed in terms of the scalar potential ¢’, we concentrate on finding the scalar potential in frames! ‘Substituting from equations (93) and (94) into equation (95), we have for the scalar potential: , 1 4 =e (97) Gneo lem] To find an expression for ¢/ in terms of coordinate in S', we use the Lorentz transformations of the coordinates. 2=7(2-w) (8) ‘Aavanced Eleivomagretism 8 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism 29 Part 9 EM and Special Relat A Moving Point Charge: The Liénard-Wiechert Potentials A Moving Poi Charge: The Lignard-Wiechert Potentials Substituting from (98) into (97) gives "i 1 a Sree [fe ve) - @—¥4)] (99) (100) Note that the charge is at coordinate 2!, at time ¢, (as measured in frame S"), and that the potentials 4" and A, are measured at. coordinate 2’ and time ¢/ (again, as measured in frame S") Since any change in the source takes time Az'/e to propagate a distance Az’, we must have: Uae, (01) Therefore, we can write equation (100) for the potential in frame § tS (102) 24] (1 v/e) where the minus sign holds for 2! > 2/, (charge moving towards ‘the observer) and the plus sign holds for 2! < 2f, (charge moving away from the observer) ‘Advanced Eleevromagretism 50 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 51 Part 9: EM and Special RelatityA Moving Point Charge: The Lignard-Wiechert Potentials Since coordinates in directions transverse to the boost are not changed by the Lorentz transformation, we can generalise ‘A Moving Point Charge: The Liénard-Wiechert Potentials Dropping the prime, we can use equations (103) and (96) to write expressions for the potentials around a point charge moving with constant velocity # = Ge: equation (102) to a boost in an arbitrary direction: (105) Nite « of (fe) — (103) z ("") = ey oma le a) 66: é 4ne0 a (Bw) 4@y = Sqn (106) where: where if is a unit vector from the charge at i to the observer er 1 er at r, and the charge is at # at time ty, given by: Sta EE vous (104) = Fy t [Fe fal (107) Equations (105) and (106) give the Liénard-Wiechert, potentials for a point charge moving at constant velocity, ‘aevanced Gicvomagretam G2 Pans Ew and Space Rom ‘Raancod Cecvonsanciom SB Peto ea and Speci Rem A Moving Point Charge: The Liénard-Wiechert Potentials From the Liénard-Wiechert potentials (105) and (106): 1 area eG) = 4e@y = eo we see that there is a relativistic enhancement of the potential for a charge moving towards an observer. and a relativistic reduction of the potential fora charge moving away from an Goserver. ‘The enhancement or reduction compared to the Static case Is‘ relativistic effect, since It vanishes in the limit eo (In which case, the expressions for the potentials around a moving point charge are the same as those for the potentials around a static charge) Finally, note that the Liénard-Wiechert potentials satisty the Lorenz gauge conaition: (108) The Electromagnetic Field The components of the magnetic field (2, By, Bz) and the electric field (Hz, Hy, Ez) cannot be combined into a four-vector. However, they can be combined into a matrix that will allow us to write Maxwell's equations in explicitly covariant form: Recall that the electromagnetic field is obtained from the derivatives of the potential. Let us define the matrix FY: re ahav ran (aos) where A¥ is the four-vector electromagnetic potential, and a is the four-vector differential operator. Since the right-hand side of equation (109) involves only four-vectors, it transforms under @ Lorentz transformation a at al — a A = NAY OPAP— NE NYgA™ (110) Therefore, the matrix ##” transforms under a Lorentz transformation as: PC = ANN’ FO qu) ‘Aavanced Elecromaoretism 55, Part 9: EM and Special RelatityThe Electromagnetic Field Since F#" transforms appropriately under Lorentz transformations, this is a valid quantity to use in explicitly covariant expressions. Now we inspect the components of FH” For example, we find that: OAs ay FL? = al 4? a? Al = = 8B, (112) ‘As another example, we find that 106, 10 226 5 2 na) céz cat © (113) We also note that the diagonal components of Fi” are zero - at Ad Pio, pe quay and that FH” is antisymmetric: pu pe (1s) The Electromagnetic Field Overall, we find that the components of FH" are: 0B. —By ~Fa/e B 0 Br ~By/e By -Be 0 —B./e Byje Byje Belo 0 pH (ate) We observe that the six independent components of the 4 x 4 antisymmetric matrix FH are the six components of the electromagnetic field The transformation prope! ties of the electromagnetic field under Lorentz transformations follow immediately from the transformation properties of the matrix FH FP = Am nS, HY (7) ‘Aavanced Eleivomagretism 56 Par 9 EM and Special Relatay ‘aavanced Liecvomagnetism 37 Part 9 EM and Special Relat The Electromagnetic Field We now have an explicitly covariant quantity F that contains © components of the electromagnetic field. If we are able to write Maxwell's equations purely in terms of FH and other quantities (four-vectors and Lorentz invariants) with the proper transformation properties, then we will have shown that Maxwell's equations are consistent with special relativity. Explicitly Covariant Form of Maxwell's Equations First, consider the expression: are (ais) This may be evaluated explicitly using equation (116); but note that we can also write it using (109) Okt” = 8,0" AY — a0" AM ais) Note that: aa" (220) In the Lorenz gauge, the four-vector potential AM satisfies the wave equation: DAY = ~poJ” (22a) We can also choose the Lorenz gauge condition uA" =0 (122) and hence: ay F HY = po)” (223) ‘Advanced Eleevromagretism 58 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 59 Part 9: EM and Special RelatityExplicitly Covariant Form of Maxwell's Equations Explicitly Covariant Form of Maxwell's Equations Consider the explicitly covariant equation (123): ayFHY = pos” (124) If we take v = 4, we find that 8 Ey tee (125) which can be written: (126) Now consider the case v= 1 in the explicitly covariant equation (123) FEY = — pod” (128) This gives: (229) which can be written Wx Ble (220) We obtain similar expressions from the cases v =2 and v= 3; combining the equations from all the cases v = 1,2,3, we Using /Hoeo, we obtain the familiar form of Maxwell's @ Horo obtain Maxwell's equation equation VB=o (227) vx i 2 (a3) a ‘evarce Wecromsgretam GPa EM ond Spd Ray ‘vanced acvorsanctam Gl Pa 8 EM and Seda Ray Explicitly Covariant Form of Maxwell's Equations Explicitly Covariant Form of Maxwell's Equations Now consider the definition of the matrix PHY = AH AY — BY AM (135) We find that the explicitly covariant equation (123): Using this definition, we find that: 8, FH” = — pio)” (232) OPH 4 YPM 4 anprr = 0 (136) gives (by considering different values of the index v), the Inhomogeneous Maxwell's equations: vVB=p (133) 4 _ ab ; vxi-S i (134) Note that this is an identity for any values of the indices 2, 4. and v: it holds for any components of the matrix FH” If we choose: A=3 37) we fing: an? fn.+Ze, ae yet ° (138) which can be written in the form familiar from Maxwell's equations: ve (439) ‘Advanced Eleevromagretism 2 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 6s Part 9: EM and Special RelatityExplicitly Covariant Form of Maxwell's Equations Now let us take the equation (136): Explicitly Covariant Form of Maxwell's Equations To summarise, the explicitly covariant equation (123) OEE 4 OPM 4 np (140) with the values for the indices: A,B HY = po” (245) eet, 2 4 (sax) can be written using three-vectors: We find that v (ase) 1a, ,18 AEB +o Bs 142) cat + cy (aaa) which can be written The explicitly covariant equation (136) Vx 8).+28.=0 (43) OEM + OPM OPO = 0 a7) a We find similar equations for = 1, and = 4; and for can be written using three-vectors: = 2, v= 3 and A= 4, Combining the equations together, we ~ = ab obtain the familiar Maxwell's equation ViB=0 VK E+ (248) of vx itt ao (say ‘aavanced tlecvomsgretm os Park EW and Specs Resta ‘aavancoa Kecvomagnetam S Part EW and Speci Reston Lorentz Transformation of the Electromagnetic Field Explicit expressions for the transformations of the electromagnetic field can be found from equation (111) P= RH NY, Fo? (as) Since the electromagnetic field #9 is represented by a matrix, and the Lorentz transformation AM, is also represented by a matrix, applying the transformation just involves matrix multiplication ‘Advanced Eleevromagretism 66 Part 9: EM and Special Relatty Lorentz Transformation of the Electromagnetic Field For a Lorentz boost of velocity v along the = axis, we find for the electric field BL = By (aso) FL = (By — vB.) (asi) = (8: + By) (52) And for the magnetic field BL = (asa) By (asa) BL (155) The inverse transformations are obtained simply by replacing » by -w Note that the electric field in the S’ frame depends on the magnetic field in the S frame; and that the magnetic field in S” depends on the electric field in S. ‘Advanced Elecromaoretism er Part 9: EM and Special RelatityLorentz Transformation of the EM Field: Example 1 ‘An stationary observer measures the Earth's magnetic field to be 30 T. What field would be measured by an observer in an aeroplane flying past the stationary observer at 900 km/h (250 m/s) perpendicular to the direction of the Earth’s field? Choose the x axis to be the direction of motion of the aeroplane, relative to the stationary observer, and the z axis to be in the direction of the magnetic field. For the stationary observer, the magnetic field is: Lorentz Transformation of the EM Field: Example 1 For the moving observer, 8 = 8.3 x 10 measured by the moving observer are: T and y= 1, The fields BL =o BL = 0 BL = 7B. x 30:7 and the electric field is: Br = 0 , By = 0 m= 0 B= 30nr By = Be 7.5 mv/m Bao and the electric field is: E. = 0 Ey = 0 B, = 0 ‘aavanced tlecvomsgretm oe ark 9 Ew ond Speci Resta ‘evanced Uecvonsaretom ° Part EW and Speci Reston Lorentz Transformation of the EM Field: Example 2 ‘A neutral hydrogen atom moves with kinetic energy 100 keV in a laboratory frame. Suppose the atom enters a magnetic field of strength 1 T perpendicular to its direction of motion. What fields will the atom experience in its rest frame? First, we calculate the velocity of the hydrogen atom. The rest mass of the hydrogen atom is mn = 0.938271 GeV/c? So the total energy of the hydrogen atom is: syne? = 0.938271 GeV + 100 keV = 0.938371 GeV (156) Hence 1 = 2938871 1 00107 (387) 0.938271 Hence (asa) and: v = Be 4.38 x 108 m/s (ass) Lorentz Transformation of the EM Field: Example 2 Let the hydrogen atom be moving along the x axis, and the magnetic field be parallel to the z axis. The initial electric field seen by the hydrogen atom is zero; the magnetic field is: Be = 0 By = 0 B. = 17 The magnetic field seen by the hydrogen atom in its rest frame BL= 0 BL = 0 BL = yB,=1000107T ‘Advanced Eleevromagretism 70 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 7 Part 9: EM and Special RelatityLorentz Transformation of the EM Field: Example 2 Lorentz Transformation of the EM Field: Example 3 The electric field seen by the hydrogen atom in its rest frame is. What are the fields around @ moving point charge? Let the charge q be moving along the + axis with velocity v. In B=o the rest frame S! of the charge, there is no magnetic field, and BL = —ywB, = 4.38 MV/m the electric field is given by: B= 0 (160) The hydrogen atom sees an electric field of over 4 megavolts In cartesian coordinates, the field components are: per meter! This is an extremely strong electric field, and can 161 result in ionisation of the hydrogen atom (an effect called 72+ Pays (161) Lorentz ionisation) Kt % aa 62) BE = (63) at Eye? ‘aavanced tlecvomsgretm 72 Park EW and Specs Resta ‘aavancoa Kecvomagnetam a Part EW and Speci Reston Lorentz Transformation of the EM Field: Example 3 Lorentz Transformation of the EM Field: Example 3 Now we apply the inverse Lorentz transformations to find the fields in the laboratory frame. Note that we have to transform the coordinates as well as the fields. 2 = e-w) (164) v v (165) dae (166) With zero magnetic field in ', the electric field transforms as: B, = Fy (167) Py = 7B) (168) B, = 7B (169) and the magnetic field transformations are: (70) a7) (172) We find that the electric field in the frame S is given by. 2 — vt) WP + Pa? en) oy was 0m) ve (75) wore Notice the factor 7 that appears in the x-dependence of the fields. This means that with increasing velocity, the fields become “flattened” towards the plane perpendicular to the direction of motion of the charge. ‘Advanced Eleevromagretism 74 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 75 Part 9: EM and Special RelatityLorentz Transformation of the EM Field: Example 3 The magnetic field is given by: Lorentz Transformation of the EM Field: Example 3 To visualise the fields, consider the fields along the axes for the case t qi Eely 0) =~, (a79) Be = (76) freq By = a77) Bylx 0) 14 (180) Gxeou Be (178) , Bxe=y=0) = -2% (asi) Enegz The magnetic field is “flattened” at high particle velocities, in and the magnetic field is given by: fe same way as the electric field. There is also a direct dependence of the size of the magnetic field on the velocity (as Be = 0 (182) we expect): at v= 0, the magnetic field vanishes altogether v4 Bie=y=0) =~ + (183) Panez B(2=2=0) (asa) ‘Ravanced tiecivomaaretam 76 Park EW and Specs Resta ‘Revancod tleiromagnetism 7 Part 9: EM and Special ReiatWiy Lorentz Transformation of the EM Field: Example 3 Summary of Part 9: Electromagnetism and Special Relativity The electric and magnetic fields around a relativistic charged particle are “flattened” towards a plane perpendicular to the direction of motion of the charged particle, ‘You should be able to ‘© Explain what is meant by a “Lorentz invariant” 1 State that electric charge is @ Lorentz invariant, and show that electric and magnetic fields are not Lorentz invariants. = write the Lorentz transformations using four-vector index notation + Write down and use the four-vector equivalents of the grad, div and Iaplacian ifferential operators. ‘+ Write down the components of the four-vectors representing current Gensity and electromagnetic potentials. + Derive 2 4 x 4 matrix representing the electromagnetic elds, by taking the “grad” of the electromagnetic potential four-vector ‘= write down Maxwell's equations and the continuity equation using four-vector notation, and show the equivalence of the equations in this form to the equations written in the usual three-vector notation, + Perform Lorentz transformations of the current density, electromagnetic potentials and electric and magnetic elds ‘Advanced Eleevromagretism 78 Part 9: EM and Special Relatty ‘Aavanced Elecromaoretism 79 Part 9: EM and Special Relatity