Lecture 24
Diunggah oleh
Anand RajHak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Lecture 24
Diunggah oleh
Anand RajHak Cipta:
Format Tersedia
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Introduction
In the earlier lectures we have used the effective properties of the unidirectional layers in the
development of various lamina or laminate mechanics issues. However, we know that at microscale
the fibrous composites are heterogeneous. A composite is made of two main phases - fiber and
matrix. Further, we know that apart from these two phases, additional phase may be present in the
composite. These phases may be fillers, zones formed due to reaction between fibre and matrix and
the coatings applied to the fiber, if any. The properties of these constituents, their amounts present
and their distribution affect the effective properties of the composite.
It is now well understood that to determine the effective properties of a composite one needs to
consider the microscale, that is, the scale at which the fibre and matrix are present. Thus, the study
of composites at the fiber and matrix level is referred to as micromechanics.
In the present lecture we will present various methods to determine the effective hygro-thermo-
mechanical properties of the composite. It is assumed that the properties of constituents, their
arrangements and amounts are known a-priori.
The Lecture Contains
Effective Elastic Constants
Idealization of Microstructure of Fibrous Composite
Volume and Mass Fractions, Density and Void Content
Mass Fractions
Density
Strength of Material Approximations
Effective Axial Modulus
Effective Axial (Major) Poison's Ratio
Effective Transverse Modulus
Homework
References
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_1.htm[8/18/2014 1:02:59 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Effective Elastic Constants:
The unidirectional lamina is interest of this course. The unidirectional lamina is orthotropic in nature.
We know from the 3D constitutive equations that an orthotropic material has 9 independent
constants. Further, for a transversely isotropic material there are 5 independent constants. The
average or effective constitutive equation for transversely isotropic material is given as below. The
transverse isotropy is in plane 2-3.
where , are the effective elastic constants of the equivalent homogeneous
material.
In this chapter, we are going to see the micromechanical methods to obtain the effective engineering
constants that define the above effective elastic constants of the equivalent homogeneous material.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_2.htm[8/18/2014 1:02:59 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Idealization of Microstructure of Fibrous Composite:
As mentioned earlier, the micromechanics is a study at fibre and matrix level. Thus, the geometry of
arrangement of the fibres and matrix in a composite is an essential requirement to develop a model
for the study. Some of the methods do not use the geometry of arrangement. Most of the methods
developed for micromechanical analysis assume that:
1. The fibers and matrix are perfectly bonded and there is no slip between them.
2. The fibres are continuous and parallel.
3. The fibres are assumed to be circular in cross section with a uniform diameter along its
length.
4. The space between the fibres is uniform throughout the composite.
5. The elastic, thermal and hygral properties of fibre and matrix are known and uniform.
6. The fibres and matrix obey Hooke’s law.
7. The fibres and the matrix are only two phases in the composite.
8. There are no voids in the composite.
There are many ways to idealize the cross section of a lamina. In Figure 7.1 are shown two popular
idealizations. The most commonly preferred arrangements are square packed and hexagonal packed
arrays of fibres in matrix. The square and hexagonal packed arrays can be as shown in Figure
7.1(a), and (b), respectively.
In these idealizations it is seen that due to symmetry and periodicity of these arrays one can
consider only one array to analyze the lamina at micro scale. Further, if this one array represents the
general arrangement of fibres with respect to matrix and the interactions of fibre and matrix phases,
then such array is called Representative Volume Element (RVE). Further, this RVE as a volume of
material statistically represents a homogeneous material. In the analysis of an RVE the boundary
conditions are chosen such that they reflect the periodicity. Thus, the arrays shown in Figure 7.1 are
various RVEs. One should be able to see that the RVE also reflects the volume fractions. The term
RVE was first coined by Hill in 1963.
For example, the square RVE represents a lower fibre volume fraction than a hexagonal RVE. Note
that RVE is also called as Unit Cell.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_3.htm[8/18/2014 1:02:59 PM]
Objectives_template
Figure 7.1: Idealization of cross section of a lamina
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_3.htm[8/18/2014 1:02:59 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Volume and Mass Fractions, Density and Void Content:
In the present section we are going to introduce some important concept of relative fraction of fibres
and matrix by volume and mass. This is very important from the point that the most of the
micromechanics based approaches use these fractions, along with the properties of individual
phases, to express the properties of the equivalent homogeneous material.
In the present case, the effective properties of a composite are obtained with the assumption that
the fibre is orthotropic or transversely isotropic and matrix is isotropic in behaviour. However, with
appropriate changes, fibre can also be considered to be isotropic. In the following, the subscripts or
superscripts and will denote fibre and matrix, respectively.
Volume Fractions:
As stated earlier, the fibre volume fraction is defined as the ratio of fibre volume to composite volume
and matrix volume fraction is defined as the ratio of matrix volume fraction to composite volume. Let,
be the volume occupied by fibres and matrix, respectively. Let, be the composite volume.
We know that,
(7.1)
Thus, from these two definitions of volume fractions, we can write
(7.2)
Thus, in notations
(7.3)
where, denotes the fibre volume fraction and denotes the matrix volume fraction. Note that
“total volume” and “composite volume” are used interchangeably.
Note: If the interphase is also present as a third phase then, Equation (7.2) is modified as
or
(7.4)
where, denotes the interphase volume fraction and denotes the interphase volume.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_4.htm[8/18/2014 1:02:59 PM]
Objectives_template
In case, there are voids present in composite, then the above equation becomes as
or
(7.5)
where, denotes the void volume fraction and denotes the void volume. In the remaining,
we will consider that there are only two phases and Equation (7.3) is used.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_4.htm[8/18/2014 1:02:59 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Mass Fractions:
Let and be the mass of fibres, matrix and composite, respectively. We know that
(7.6)
The mass fractions, similar to volume fractions, are defined as the ratio of mass of respective phase
to the mass of composite. Thus, we can write,
(7.7)
where, is fibre mass fraction and is matrix mass fraction. Now, let us write the mass of
each phase in terms of density and volume of respective phase as
(7.8)
where, and are the densities of fibre, matrix and composite, respectively. Now, mass
fractions can be written in terms of density and volume fractions as
(7.9)
This relation between mass and volume fractions is given in terms of individual constituent properties
(using Equations (7.6) and (7.8)) as
(7.10)
Thus, it is clear from the above equation that the volume and mass fractions are not the same. One
should always state the basis for calculating the fibre content in a composite.
Density:
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_5.htm[8/18/2014 1:03:00 PM]
Objectives_template
The density of composite is derived in terms of densities and volume fractions of the individual
phases as follows. The mass of composite is given by Equation (7.6). We can write this in terms of
respective volume fractions and densities (with rearrangement) as
(7.11)
This is written using the definition of volume fraction for fibre and matrix as
(7.12)
We will write the density of composite in terms of mass fraction from Equation (7.9) as
(7.13)
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_5.htm[8/18/2014 1:03:00 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Strength of Material Approximations:
In general, the laminates made are thin. Hence, for such laminates the analysis done using Kirchhoff
and plane stress assumptions is reasonably good. For such analysis, one needs the engineering
constants that occur in defining planar constitutive equations. These engineering constants are:
1. - the axial modulus
2. = - transverse modulus
3. - axial Poisson’s ratio (for loading in - direction)
4. - axial shear modulus (shear stress parallel to the fibers)
Further, it is seen that for transversely isotropic composite, four out of five (the fifth one is )
properties can be developed from this approach. For the planar hygro-thermal analysis of such
laminates, one can also obtain the in-plane coefficients of thermal expansions and and
hygroscopic expansion and as well.
It is important to note that this approach involves assumptions which do not necessarily satisfy the
requirements of an exact elasticity solution. In this approach the effective properties will be
expressed in terms of the elastic properties and volume fractions of the fiber and matrix. The lamina
is considered to be an alternate arrangement of fibres and matrix. The RVE chosen in these
derivations is shown in Figure 7.2. The RVE here does not take into account the cross sectional
arrangement of fibres and matrix, rather it represents volume of the material through the cross
sectional area of fibre and matrix.
Figure 7.2: (a) Unidirectional lamina, (b) RVE for unidirectional composite for
prediction of elastic properties
Let, and represent fibre area and matrix area, respectively. and represent fibre
and matrix widths, respectively. be the length of the RVE.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_6.htm[8/18/2014 1:03:00 PM]
Objectives_template
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_6.htm[8/18/2014 1:03:00 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Effective Axial Modulus :
The unit cell as shown in Figure 7.2 is used to compute the effective axial modulus . It should be
noted that the thickness of the unit cell is not important in this computation. Further, the cross
sectional shapes are not considered in this calculation. However, the cross sectional areas are
important in this calculation. The thicknesses of the fibre and matrix constituents are same in the unit
cell. Hence, the areas of the constituents represent the volume fractions of the constituents.
In the calculation of effective axial modulus, it is assumed that the axial strain in the composite is
uniform such that the axial strains in the fibers and matrix are identical. This assumption is justified
by the fact that the fibre and the matrix in the unit cell are perfectly bonded. Hence, the elongation in
the axial direction of the fibre and matrix will also be identical. Thus, the strains in the fibre and
matrix can be given as
(7.14)
where, is the axial strain in the composite and and are the axial strains in fibre and
matrix, respectively. Now, let and be the axial Young’s moduli of the fibre and matrix,
respectively. We can give the axial stress in the fibre, and matrix, as
(7.15)
Using the above equation and the cross section areas of the respective constituent in the unit cell,
we can calculate the forces in them as
(7.16)
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_7.htm[8/18/2014 1:03:00 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
The total axial force in the composite is sum of the axial forces in fibre and matrix. Thus, the total
axial force in the composite substituting the expressions for axial strains in fibre and matrix from
Equation (7.14) in above equation, can be given as
(7.17)
Now be the average axial stress in composite. The total cross sectional area of the composite is
. Thus, using the average axial stress and cross sectional area of the composite, the
axial force is
(7.18)
Thus, combining Equation (7.17) and Equation (7.18) and rearranging, we get
(7.19)
Figure 7.3: (a) Undeformed unit cell under (b) and (c) deformed individual
constituents of the unit cell
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_8.htm[8/18/2014 1:03:00 PM]
Objectives_template
Let us define
(7.20)
Further, noting that the ratios and for same length of fibre and matrix represent the fibre
and matrix volume fractions, respectively. Thus, combining Equations (7.19) and (7.20), we get
(7.21)
The above equation relates the axial modulus of the composite to the axial moduli of the fibre and
matrix through their volume fractions. Thus, the effective axial modulus is a linear function of the
fiber volume fraction. This equation is known as rule of mixtures equation. It should be noted that the
effective properties are functions of the fiber volume fractions; hence it should always be quoted in
reporting the effective properties of a composite.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_8.htm[8/18/2014 1:03:00 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Effective Axial (Major) Poison’s Ratio :
To determine the effective axial Poisson’s ratio we consider the loading as in the case applied for
determining the effective axial modulus. Here, for this loading we have and other stresses
are zero. We define the effective axial Poisson’s ratio as
(7.22)
The effective strain in direction 2 from Figure 7.3(b) and (c) can be given as
(7.23)
Now, the changes in and can be obtained using the Poisson’s ratio of individual
constituents. The axial Poisson’s ratios for fibre and matrix are given as
(7.24)
Thus, the changes in and are given as
(7.25)
The total change in is given as
(7.26)
The strain in direction 2 for the composite can be given using Equation (7.25) and Equation (7.26)
as
(7.27)
Here, and denote the fibre and matrix volume fractions for same length of fibre and
matrix. Note that denotes the effective axial strain . Thus, from Eq. (7.27) the effective axial
Poisson’s ratio is written as
(7.28)
The above equation is the rule of mixtures expression for composite axial Poisson’s ratio.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_9.htm[8/18/2014 1:03:00 PM]
Objectives_template
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_9.htm[8/18/2014 1:03:00 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Effective Transverse Modulus :
Here, we are going to derive the effective transverse modulus by loading the RVE in direction 2 as
shown in Figure 7.4(a). There are two considerations while deriving this effective modulus. The first
approach considers that the deformation of the each constituent is independent of each other as
shown in Figure 7.4(b) and (c) and the deformation in direction 1 is not considered. The second
approach considers that deformations of the fibre and matrix in direction 1 are identical as they are
perfectly bonded.
is applied to the RVE as shown in
To calculate the effective modulus in direction 2, a stress
Figure 7.4(a).
First Approach:
As mentioned, the fibre and matrix deform independently of each other. The resulting deformation in
direction 1 is not considered here. This assumption is simplistic and was used by early researchers.
The fibre and matrix are subjected to same state of stress. The state of stress is unidirectional, that
is, . Now, using the individual moduli and deformations in direction 2, these
stresses can be given as
(7.29)
From this equation we can write the individual deformations, which give the total deformation in
direction 2 as
(7.30)
Now, the composite strain in direction 2 can be calculated from the definition as
(7.31)
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_10.htm[8/18/2014 1:03:01 PM]
Objectives_template
Figure 7.4: (a) Undeformed unit cell under uniform stress (b) and (c)
deformed individual constituents of the unit cell
Introducing the volume fractions in the above equation,
(7.32)
Noting that , from the above equation, we get
(7.33)
This equation is the rule of mixtures equation for effective modulus .
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_10.htm[8/18/2014 1:03:01 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
Home Work:
1. What are the assumptions in a typical micromechanical analysis?
2. Write a short note on RVE/Unit Cell.
3. Define volume and mass fractions for fibre and matrix and derive expressions for them.
4. Derive an expression for density of a composite in terms of densities of its constituents.
5. Using strength of materials approach, derive expressions for effective axial modulus, Poisson’s
ratio and transverse modulus.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_11.htm[8/18/2014 1:03:01 PM]
Objectives_template
Module 7: Micromechanics
Lecture 24: Strength of Materials Approach
References:
R Hill. Elastic properties of reinforced solids: some theoretical principles. J. Mech.
Phys. Solids, 1963, Vol. 11, pp. 357-372.
SW Tsai, HT Hahn. Introduction to Composite Materials, Technomic Publishing,
Lancaster, PA, 1980.
MW Hyer, AM Waas. Micromechanics of linear elastic continuous fibre composites, in
Comprehensive Composite Materials. Vol. 1: Fiber Reinforcements and General Theory
of Composites, Eds. Kelly A, Zweben C. Elsevier 2000.
CT Herakovich. Mechanics of Fibrous Composites, John Wiley & Sons, Inc. New York,
1998.
AK Kaw. Mechanics of Composite Materials. 2nd Edition, CRC Press, New York, 2006.
file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture24/24_12.htm[8/18/2014 1:03:01 PM]
Anda mungkin juga menyukai
- Shoe Dog: A Memoir by the Creator of NikeDari EverandShoe Dog: A Memoir by the Creator of NikePenilaian: 4.5 dari 5 bintang4.5/5 (537)
- Grit: The Power of Passion and PerseveranceDari EverandGrit: The Power of Passion and PerseverancePenilaian: 4 dari 5 bintang4/5 (587)
- Numerical Simulation of Prestressed Precast Concrete Bridge Deck Panels Using Damage Plasticity ModelDokumen10 halamanNumerical Simulation of Prestressed Precast Concrete Bridge Deck Panels Using Damage Plasticity ModelAnand RajBelum ada peringkat
- Mathcentre Ode PDFDokumen2 halamanMathcentre Ode PDFRavi TejBelum ada peringkat
- Hex Tet ComparisonDokumen13 halamanHex Tet ComparisonajimonBelum ada peringkat
- De ApplicationsDokumen174 halamanDe ApplicationsnoteasytobebooBelum ada peringkat
- Formula SheetDokumen1 halamanFormula SheetSaleem SheikhBelum ada peringkat
- Class Xii - Differntiation & Integration Formulae.Dokumen1 halamanClass Xii - Differntiation & Integration Formulae.Mandeep Singh Plaha59% (22)
- DynamicsDokumen31 halamanDynamicsANAND RAJBelum ada peringkat
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDari EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RacePenilaian: 4 dari 5 bintang4/5 (890)
- The Yellow House: A Memoir (2019 National Book Award Winner)Dari EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Penilaian: 4 dari 5 bintang4/5 (98)
- The Little Book of Hygge: Danish Secrets to Happy LivingDari EverandThe Little Book of Hygge: Danish Secrets to Happy LivingPenilaian: 3.5 dari 5 bintang3.5/5 (399)
- On Fire: The (Burning) Case for a Green New DealDari EverandOn Fire: The (Burning) Case for a Green New DealPenilaian: 4 dari 5 bintang4/5 (73)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDari EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifePenilaian: 4 dari 5 bintang4/5 (5794)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDari EverandNever Split the Difference: Negotiating As If Your Life Depended On ItPenilaian: 4.5 dari 5 bintang4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDari EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FuturePenilaian: 4.5 dari 5 bintang4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDari EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryPenilaian: 3.5 dari 5 bintang3.5/5 (231)
- The Emperor of All Maladies: A Biography of CancerDari EverandThe Emperor of All Maladies: A Biography of CancerPenilaian: 4.5 dari 5 bintang4.5/5 (271)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDari EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You ArePenilaian: 4 dari 5 bintang4/5 (1090)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDari EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyPenilaian: 3.5 dari 5 bintang3.5/5 (2219)
- Team of Rivals: The Political Genius of Abraham LincolnDari EverandTeam of Rivals: The Political Genius of Abraham LincolnPenilaian: 4.5 dari 5 bintang4.5/5 (234)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDari EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersPenilaian: 4.5 dari 5 bintang4.5/5 (344)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDari EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaPenilaian: 4.5 dari 5 bintang4.5/5 (265)
- Rise of ISIS: A Threat We Can't IgnoreDari EverandRise of ISIS: A Threat We Can't IgnorePenilaian: 3.5 dari 5 bintang3.5/5 (137)
- The Unwinding: An Inner History of the New AmericaDari EverandThe Unwinding: An Inner History of the New AmericaPenilaian: 4 dari 5 bintang4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Dari EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Penilaian: 4.5 dari 5 bintang4.5/5 (119)
- Her Body and Other Parties: StoriesDari EverandHer Body and Other Parties: StoriesPenilaian: 4 dari 5 bintang4/5 (821)
- Setting up PCR for D1S80 VNTR Analysis from Buccal Cell DNADokumen10 halamanSetting up PCR for D1S80 VNTR Analysis from Buccal Cell DNAmmarrinnaBelum ada peringkat
- FTIR Analysis of Rapeseed Oil and Biodiesel Methyl EstersDokumen2 halamanFTIR Analysis of Rapeseed Oil and Biodiesel Methyl Estersrgx1120% (1)
- Combustion Theory Ideal Gas ModelDokumen74 halamanCombustion Theory Ideal Gas ModelAli ÇelikBelum ada peringkat
- Niton XRF V Fire Assay App NoteDokumen2 halamanNiton XRF V Fire Assay App Notedarioharloc2272Belum ada peringkat
- CH 5 Heat Exchanger Design MethodsDokumen30 halamanCH 5 Heat Exchanger Design Methodsapi-3765936100% (1)
- Amb Jul Aug 2015Dokumen100 halamanAmb Jul Aug 2015unitymineBelum ada peringkat
- Line Sizing CriteriaDokumen5 halamanLine Sizing CriteriaBILAL ILYASBelum ada peringkat
- The Radio Chemistry of Mercury - Us AECDokumen211 halamanThe Radio Chemistry of Mercury - Us AEClondonbluetopazBelum ada peringkat
- Practical of Chemistry PDFDokumen377 halamanPractical of Chemistry PDFrajesh971Belum ada peringkat
- ASTM C128 Standard Test Method for Relative Density and AbsorptionDokumen23 halamanASTM C128 Standard Test Method for Relative Density and AbsorptionLC LeeBelum ada peringkat
- Dual Shield II 70T-12H4: Gas-Shielded Flux-Cored Wires (Fcaw) Mild Steel WiresDokumen2 halamanDual Shield II 70T-12H4: Gas-Shielded Flux-Cored Wires (Fcaw) Mild Steel WiresPhilippe TrudelBelum ada peringkat
- Plastics: Name: Taaha Muzaffar Imam ROLL NO.: 19011AA002 Sem/Sec: Ii/A Branch: B.Arch College: Spa' JnafauDokumen5 halamanPlastics: Name: Taaha Muzaffar Imam ROLL NO.: 19011AA002 Sem/Sec: Ii/A Branch: B.Arch College: Spa' JnafauTaaha Muzaffar ImamBelum ada peringkat
- Anaerobic Fundamentals COD BalanceDokumen28 halamanAnaerobic Fundamentals COD BalanceDavid Sanchez100% (1)
- AntimonyDokumen72 halamanAntimony沈益Belum ada peringkat
- Brittany L. Hayes - Recent Advances in Microwave - Assisted SynthesisDokumen11 halamanBrittany L. Hayes - Recent Advances in Microwave - Assisted SynthesisnnnnjwBelum ada peringkat
- Quantitative Analysis of Carbohydrates I - Lab 4Dokumen27 halamanQuantitative Analysis of Carbohydrates I - Lab 4Noriko Medoruma0% (3)
- Analisis de Gas de Aceite de Transformador Utilizando Una Columna de Separacion Astm d3612 KasalabDokumen2 halamanAnalisis de Gas de Aceite de Transformador Utilizando Una Columna de Separacion Astm d3612 KasalabJohnatan HernándezBelum ada peringkat
- Nova Hunting The Elements Video GuideDokumen3 halamanNova Hunting The Elements Video GuideJaclyn Dugger100% (1)
- Pipe identification color codingDokumen1 halamanPipe identification color codingขุน แสนBelum ada peringkat
- Ex: # 01: A Sample of Dry Anthracite Has The Following: 44kg CODokumen12 halamanEx: # 01: A Sample of Dry Anthracite Has The Following: 44kg COnicoolBelum ada peringkat
- Rambutan SunscreenDokumen7 halamanRambutan SunscreenAndrea Alvarado RoBelum ada peringkat
- Xanthan Gum-USPDokumen2 halamanXanthan Gum-USPLaboratorium FarmasiBelum ada peringkat
- Laprak Distilasi UapDokumen11 halamanLaprak Distilasi UapRetnani Arum PertiwiBelum ada peringkat
- Test Report E-Liquid: 1 Sample InformationDokumen10 halamanTest Report E-Liquid: 1 Sample InformationVangel PetrovBelum ada peringkat
- Sludge Dewatering PDFDokumen36 halamanSludge Dewatering PDFPaul Maposa100% (2)
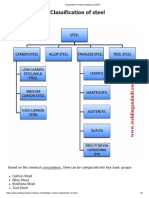
- Classification of Steel - Welding and NDTDokumen3 halamanClassification of Steel - Welding and NDTAshif Iqubal100% (1)
- Top Steel Companies in IndiaDokumen3 halamanTop Steel Companies in Indiazukmos67% (3)
- API 651 QuestionsDokumen4 halamanAPI 651 QuestionsMohammed YoussefBelum ada peringkat
- Enhanced Hybrid Science 6 Quarter1 Module 1 Week1Dokumen10 halamanEnhanced Hybrid Science 6 Quarter1 Module 1 Week1KATHLENE CORPUS100% (1)
- Experiment 2: Brinell Hardness TestDokumen5 halamanExperiment 2: Brinell Hardness TestseifBelum ada peringkat