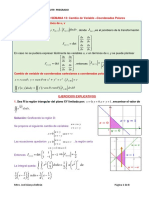
SESIÓN 01: INTRODUCCIÓN A VECTORES Y

TENSORES
ii  j  j  k  k  0
i j  k   ji
1. VECTORES Y OPERACIONES
VECTORIALES v1  v2  (u1i  v1 j  w1k )  (u2i  v2 j  w2 k )
u   (u1u2i  i  u1v2i  j  u1w2i  k
v   v  , v  u v w
T
v1u2 j  i  v1v2 j  j  v1w2 j  k
 w
 w1u2 k  i  w1v2 k  j  w1w2 k  k
v  u v w2 2 2
 (v1w2  v2 w1 )i  (u1w2  u2 w1 ) j  (u1v2  u2v1 )
Se puede usar la notación determinante:
v1  u1i  v1 j  w1k  i j k  v1w2  v2 w1 
 v1  v2  (u1  u2 )i  (v1  v2 ) j  ( w1  w2 )k
v2  u2i  v2 j  w2 k 
 v1  v2  u1 v1 w1  u1w2  u2 w1 
 su  u2 v2 w2  u1v2  u2v1 

sv  s(ui  vj  wk )  sui  svj  swk   sv  
EL TRIPLE PRODUCTO ESCALAR
 sw u v w
1 1 1

EL PRODUCTO PUNTO DE DOS v1  v2  v3   u2 v2 w2

VECTORES
El producto punto de dos vectores v1 y v2 es u3 v3 w3
una cantidad escalar dada por:

v1  v2  v1 v2 cos(v1 , v2 )
i i  j  j  k  k  1
i  j  i  k  j i  j  k  k i  k  j  0
v1  v2  (u1i  v1 j  w1k )  (u2i  v2 j  w2 k )
v1  v2  u1u2  v1v2  w1w2
Un vector unitario ev en la dirección de v es:

v
ev 
GRADIENTE DE UN ESCALAR Y DERIVADA
DIRECCIONAL
v   
 i j k
La proyección del vector v1 sobre el vector
dirección unitario de v2 x y z
s s s
s  i  j k
x y z
La proyección de s en cierta dirección del

vector unitario el está dada por:

ds
 s  el  s cos(s, el )
dl
Y se denomina derivada direccional de s a lo
largo de la dirección del vector unitario el ,
EL PRODUCTO CRUZ DE DOS VECTORES

v3  v1  v2  v1 v2 sin(v1 , v2 ) ,

y la dirección está dado por la regla de la

mano derecha.
 a111  a122   a1N N  b1
a211  a222   a2 N N  b2

aN 11  aN 22   aNN N  bN

Y la notación matricial de este sistema de
ecuaciones equivale a:
 a11 a12 a1N   1   b1 
a a22 a2 N   2   b2 
 21 
    
    
 aN 1 aN 2 aNN  N  bN 
O en su forma compacta:
A  B
OPERACIONES CON EL OPERADOR
NABLA AUTOVECTORES Y AUTOVALORES
divergente del vector En general, los auto-vectores de una matriz
u v w cuadrada A de orden N se obtienen
v    resolviendo la siguiente ecuación:
x y z Av   v  Av   I v  ( A   I )v  0
Dado que, por definición, los auto-vectores son
El divergente del gradiente de una variable no nulos, entonces:
escalar s, es denotado por el laplaciano de
un escalar s y es un escalar dado por: A   I  0  det( A   I )  0 , y en
s s s
2 2 2 forma extendida:
  (s)  2 s     a11   a12 a1N 
x 2 y 2 z 2  a 
a22   a2 N
det  21 0
El laplaciano de un vector, es un vector dado
por:
 
 2 v  ( 2u )i  ( 2 v) j  ( 2 w)k  
 aN 1 aN 2 aNN  
La curvatura de un campo vectorial
  
v  ( i j  k )  (ui  vj  wk )
x y z
i j k
   w v u w v u
  (  )i  (  ) j  (  )k
x y z y z z x x y
u v w

La divergencia de un vector v con su

gradiente
  
(v )v   (ui  vj  wk )  ( i  j  k )(ui  vj  wk )
  x y z
  
 (u  v  w )(ui  vj  wk )
x y z
u u u v v v w w w
 (u  v  w )i  (u  v  w ) j  (u v  w )k
x y z x y z x y z

Si s es una función escalar, y v1, v2 y v3 son

campos vectoriales:

Uso de matrices para describir sistemas de

ecuaciones
Un sistema de N ecuaciones y N incógnitas se
puede escribir como:
  XX  XY  XZ   u   XX u  XY v  XZ w
3. TENSORES Y OPERACIONES
TENSORIALES

 XX  XY  XZ    v    YX  YY  YZ   v    YX u  YY v  YZ w
  
   YX  YY  YZ   ZX  ZY  ZZ   w  ZX u  ZY v  ZZ w
 ZX  ZY  ZZ  De manera similar, la divergencia de un tensor
 es un vector dado por:
 XX  YX  ZX   
     (   )i  ( XY  YY 
x y z x y 
El doble producto punto de dos tensores
 y v es un escalar calculado como:

 u
 ii 
 ii XX  ij XY  ik XZ    x
   u
( : v)   ji YX  jj YY  jk YZ   :  ji  j
 ki  kj  y
 ZX  kk ZZ  
 u
ZY

 ki  k
 z
  ii XX  ij XY  ik XZ  ji YX  jj YY  jk YZ  ki ZX  kjyZYrealizando
Expandiendo
 kk ZZel producto de doble

vv  (ui  vj  wk )(ui  vj  wk )

punto, por ejemplo:
u u u u
 uu j XY
uv : jiuw   i j : j i XY  i  i  XY   XY
 iiuu  ijuv  ikuw
 jivu  jjvv  jkvw


   vv vw 
  vv   vuRealizando
y 1
y 1
los mismos pasos en cada término
y y

 wudel producto
wv ww 
expandido se obtiene:
 u u u v v
 kiwu  kjwv  kkww  ( : v)   XX   XY   XZ   YX   YY
El gradiente de un vector v es un tensor
x y z x y
dado por:
TEOREMA DE LA GRADIENTE PARA

 
v  (

x
i

y

z

j  k )(ui  vj  wk )  INTEGRAL DE LINEA
Este teorema relaciona una integral de línea
con  uvalores w  en sus extremos.
vde función
 los
Sea C es una curva lisa,descrita por el vector
u v w  x x x
 ii  ij  ik  r (t) ur[ x(tv), y(tw),z (t )] / a  t  b ,
x
u
x
v
x
w
 
  v y s es

   
y y y  cuyo gradiente s
una función escalar
 ji  jj  jk , es  
continuo en C, entonces:
y y y  u dr vs(r(bw))  s((r (a))
  
 s
u v w   z z z 
 ki  kj  kk
z z z 
La multiplicación de un tensor 
por un
escalar s resulta en un tensor cuyos
componentes son multiplicado por dicho
escalar.
El producto punto de un tensor 
por un

vector v da como resultado el siguiente

vector:
 ii  ij XY  ik XZ  ji YX  jj YY 
  v    XX   (ui  vj  wk )
 
  jk YZ  ki ZX  kj ZY  kk ZZ  TEOREMA DE GREEN
Que al expandirse y resolverse se convierte Este teorema expresa la integral de contorno
en: de una curva simple cerrada C en términos de
la integral doble de la región bidimensional R
  v   (iXX u   XY v   XZ w)i  ( YX u   YY v   YZ wlimitada  ZXC.u   ZY v   ZZ w)k
) j  (por
  Sea C el contorno cerrado de una región
La ecuación anterior puede obtenerse usando
la multiplicación matricial como: bidimensional R. Si u ( x, y ) y v ( x, y ) son
funciones de las derivadas parciales continuas
definidas en R, entonces:

dv du
 (udx  vdy)   (
C R
 )dxdy
dx dy
En la ecuación xx, la integral de contorno a lo
largo de C es positiva en el sentido contrario a
las agujas del reloj.
El teorema de Green puede escribirse en una
forma más compacta usando vectores. Con
ese fin se define dr ,v y el vector de área
d S como:
d r  dxi  dyj / v  ui  vj / d S  dxdyk
Entonces la forma vectorial del teorema de
Green está dada por:
 v  d r   [  v]  d S
C R
El teorema de Green es útil para calcular
integrales de línea que surgen en flujos.
*Por formula:
3 1
 sin  d    sin 2 
4
8 4
Demostrada en:
https://www.youtube.com/watch?v=KdDXfkjGF
I8
TEOREMA DE STOKES
El teorema de Stokes es una versión
dimensional superior del teorema de Green.
Mientras que el teorema de Green relaciona
una integral de línea con una integral doble, el
teorema de Stokes relaciona una integral de
línea con una integral de superficie.
Sea v un campo vectorial, S una superficie
orientada, y C la curva contorno de S ,
orientada usando la regla de la derecha, como
se muestra en la figura xx. El teorema de
Stokes dice lo siguiente:
 [  v]  d S   v  d r
S C
Donde r es tal que d r / ds es el vector
tangente unitario y s la longitud de arco de C.
La curva de la integral de línea, C, debe tener
orientación positiva, lo que significa que los
puntos dr tienen sentido antihorario cuando
la superficie normal, d S , apunta hacia el
espectador, siguiendo la regla de la mano
derecha.
TEOREMA DE LA DIVERGENCIA
Sea V un volumen en el espacio tridimensional
de contorno S. Sea n el vector normal
unitario que apunta hacia el exterior de S. Si
v es un campo vectorial definido en V,
entonces el teorema de la divergencia
(también conocido como teorema de Gauss)
afirma que:
 [  v]dV   v  ndS
V S
1
sin 4  C
32
El teorema de divergencia implica que el flujo
neto de un campo vectorial a través de una
superficie cerrada es igual al volumen total de
todas las fuentes sumideros (es decir, la
integral de volumen de su divergencia) sobre
la región dentro de la superficie. Es un
teorema importante para la dinámica de
fluidos.
El teorema de la divergencia se puede utilizar
en diferentes contextos para derivar muchas
otras identidades útiles (corolarios).
Específicamente puede aplicarse al producto
de una función escalar s, y un vector constante
no nulo, para derivar la siguiente relación:
 [s]dV   sd S
V S
El teorema de la divergencia es igualmente
aplicable a los tensores, en cuyo caso se
escribe como:
 [  ]dV   [  n]dS
V S
REGLA INTEGRAL DE LEIBNIZ
La regla integral de Leibniz da una fórmula
para diferenciar una integral definida cuyos
límites son funciones de la variable diferencial.
Sea  ( x, t ) una función que depende de
una variable de espacio x y tiempo t. Entonces
la regla integral de Leibniz puede ser escrita
como:
  b a
b (t ) b (t )
d

dt a (t )
 ( x, t )dt  
a (t )
t
dx   (b(t ), t )   (a(t ), t )
t t
II tèr min o III tèr min o
I tèr min o

El significado de los diversos términos de la

ecuación xx pueden deducirse de la figura xx.
El primer término a la derecha da el cambio en
la integral porque  está cambiando con el
tiempo t, mientras que el segundo y tercer
términos explican la ganancia y pérdida de
área cuando los límites superior e inferior se
mueven, respectivamente.

*demostración:
https://www.youtube.com/watch?v=iueiHCw7s
Ac