101 – Matemáticas I : Cálculo diferencial en IR

Tema 10
Funciones derivables

10.1 Derivada de una función en un punto

Definición 224.- Se dice que f : (a, b) −→ IR es derivable en el punto x0 ∈ (a, b) si

f (x) − f (x0 )
lı́m = L ∈ IR
x→x0 x − x0
f (x+h)−f (x)
es decir, si existe y es finito ese lı́mite (ó el lı́mite equivalente, lı́m h ).
h→0
df
Al valor de dicho lı́mite se lo denomina derivada de f en el punto x0 y se representa por f 0 (x0 ) ó dx (x0 ).

La derivada nos indica lo que “crece” la función alrededor del y = f (x0 ) + f 0 (x0 )(x − x0 )
punto, puesto que en el cociente usado para definirla nos apa-
rf (x)
rece el incremento f (x) − f (x0 ) de la función en relación con el ¾
incremento x − x0 de la variable. f (x) − f (x0 )
El valor del cociente f (x)−fx−x0
(x0 )
, para cada x , es la pendiente
r α
de la cuerda entre los puntos (x0 , f (x0 )) y (x, f (x)) (ver figura f (x0 )
| {z }
aneja), por lo que en el lı́mite se obtendrá la pendiente de la recta x−x0 f (x)−f (x0 )
x−x0 = tg α
tangente a la gráfica de la función en el punto. Es decir, la recta
x0 ←← x
y = f (x0 ) + f 0 (x0 )(x − x0 ) resulta ser la recta tangente a la
gráfica de f en el punto (x0 , f (x0 )) .
Diremos que f : A −→ IR es derivable en un conjunto A1 ⊆ A, si lo es en cada punto de A1 . Entonces, se
puede construir la función que asocia a cada punto x ∈ A1 la derivada de la función f en el punto x; A esta
función se le llama función derivada de f y se le representa por f 0 , donde f 0 : A1 −→ IR .
Si a su vez, f 0 : A1 −→ IR es derivable en un conjunto A2 ⊆ A1 , se puede construir la derivada de la función
0
f en cada punto x ∈ A2 . A esta función se le llama función derivada segunda de f y se le representa por
(f 0 )0 = f 00 , donde f 00 : A2 −→ IR . Análogamente se tienen la derivadas de órdenes superiores, f 000 , . . . , f n) .

Ejemplo ? La función constante f : IR −→ IR , con f (x) = k , es derivable en cada punto de su dominio:

f (x)−f (x0 ) k−k 0
lı́m x−x0 = lı́m x−x = lı́m x−x = 0 = f 0 (x0 ) ; con lo que f 0 (x) = 0 para todo x ∈ IR .
x→x0 x→x0 0 x→x0 0

? La función identidad f : IR −→ IR , con f (x) = x , es derivable en cada punto de IR :

lı́m f (x0 +h)−f
h
(x0 )
= lı́m x0 +h−x
h
0
= lı́m 1 = 1 = f 0 (x0 ), y f 0 (x) = 1 para todo x ∈ IR .
h→0 h→0 h→0

? La función polinómica f : IR −→ IR dada por f (x) = x2 es derivable en cada punto de su dominio pues
x2 −x2
lı́m f (x)−f
x−x0
(x0 )
= lı́m x−x00 = lı́m (x−xx−x
0 )(x+x0 )
= lı́m x + x0 = 2x0 = f 0 (x0 ), y f 0 (x) = 2x en IR .
x→x0 x→x0 x→x0
0 x→x0

? La exponencial f (x) = e es derivable en cada punto de IR y f 0 (x) = ex , pues

x
x+h x x h h h
lı́m e h−e = lı́m e (eh −1) = lı́m ex ( e h−1 ) = ex lı́m e h−1 = ex · 1 = ex = f 0 (x).
h→0 h→0 h→0 h→0

? f (x) = ln x, es derivable en (0, +∞) y f (x) = x1 0

ln( x+h
x ) ln(1+ h ) ln(1+ h
x)
lı́m ln(x+h)−ln(x)
h = lı́m h = lı́m x h x = x1 lı́m h = 1
x = f 0 (x) .
h→0 h→0 h→0 x h→0 x

? La función f (x) = sen x es derivable en cada punto de IR y f 0 (x) = cos x

sen(x+h)−sen(x) (1) 2 sen( h h
2 ) cos(x+ 2 ) sen( h
2)
lı́m h = lı́m h = lı́m cos(x + h2 ) h = cos(x) · 1 = cos x = f 0 (x) .
h→0 h→0 h→0 2

(1) sen x−sen y = sen( x+y

2 + x−y x+y
2 ) − sen( 2 − x−y
2 ) ³ ´
= sen( 2 ) cos( 2 ) + cos( 2 ) sen( x−y
x+y x−y x+y
2 ) − sen( x+y x−y x+y x−y
2 ) cos( 2 ) − cos( 2 ) sen( 2 ) = 2 cos( x+y x−y
2 ) sen( 2 )

Prof: José Antonio Abia Vian I.T.I. en Electricidad

102 – Matemáticas I : Cálculo diferencial en IR 10.1 Derivada de una función en un punto

? La función f (x) = cos x es derivable en cada punto de IR y f 0 (x) = − sen x

cos(x+h)−cos(x) (2) −2 sen( h h
2 ) sen(x+ 2 ) sen( h
2)
lı́m h = lı́m h = lı́m − sen(x + h2 ) h = − sen(x) = f 0 (x).
h→0 h→0 h→0 2

(2) Análogamente al caso del seno, cos x − cos y = cos( x+y

2 + x−y
2 ) − cos( x+y
2 − x−y
2 ) = −2 sen( x+y x−y
2 ) sen( 2 )

? La recta y = cos 0 − sen 0(x − 0) = 1 es la recta tangente a cos(x) en el punto 0. Análogamente, la

recta y = sen 0 + cos 0(x − 0) = x es la tangente a sen(x) en el 0. 4

f (x)−f (x0 )
Para que una función sea derivable, debe existir lı́m x−x0 . Ahora bien, el denominador siempre
x→x0
tiende hacia 0, por lo que sólo¯ puede existir ¯ el lı́mite si el lı́mite del denominador también es cero; puesto que
¯ f (x)−f (x0 ) ¯
si f (x) − f (x0 ) 6→ 0 entonces ¯ x−x0 ¯ −→ ∞ o no existe. Luego debe cumplirse que lı́m f (x) = f (x0 ), es
x→x0
decir que f sea continua en x0 :
Teorema 225.- Si f es derivable en un punto x0 entonces f es continua en dicho punto.
Demostración:
Veamos que lı́m f (x) = f (x0 ) . Para cada x 6= x0 , la función f (x) puede escribirse en la forma
x→x0

f (x) = f (x) − f (x0 ) + f (x0 ) = f (x)−f

x−x0
(x0 )
(x − x0 ) + f (x0 ),
y tomando lı́mites se prueba la continudad de f en x0 , ya que:
f (x) − f (x0 )
lı́m f (x) = lı́m · lı́m (x − x0 ) + lı́m f (x0 ) = f 0 (x0 ) · 0 + f (x0 ) = f (x0 ).
x→x0 x→x0 x − x0 x→x0 x→x0

Nota: Como consecuencia de este resultado una función sólo puede ser derivable en los puntos de continuidad.
Pero la continuidad no garantiza la derivación:
Ejemplo La función f (x) = |x| es continua pero no derivable en 0, ya que
f (x)−f (0) |x| x f (x)−f (0) |x| −x
lı́m x−0 = lı́m+ x = lı́m+ x =1 y lı́m x−0 = lı́m− x = lı́m− x = −1 4
x→0+ x→0 x→0 x→0− x→0 x→0

Como para los lı́mites y la continuidad, la derivabilidad se extiende bien mediante las operaciones con
funciones:
Propiedades 226.- Sean f y g funciones derivables en un punto x0 , entonces:
a) f + g es derivable en x0 y (f + g)0 (x0 ) = f 0 (x0 ) + g 0 (x0 ).

b) f g es derivable en x0 y (f g)0 (x0 ) = f 0 (x0 )g(x0 ) + f (x0 )g 0 (x0 ).

f 0 (x0 )g(x0 ) − f (x0 )g 0 (x0 )
c) f /g es derivable en x0 , si g(x0 ) 6= 0 , y (f /g)0 (x0 ) = ³ ´2 . .
g(x0 )

Ejemplos ? Si g derivable en x0 y k una constante, f (x) = k g(x) es derivable en x0 y f 0 (x0 ) = k g 0 (x0 ).

En efecto, basta aplicar la fórmula del producto, f 0 (x0 ) = 0g(x0 ) + k g 0 (x0 ) = k g 0 (x0 ).
? La función f (x) = x3 es derivable en cada x ∈ IR , por ser producto de funciones derivables.
f (x) = x3 = x2 x = g(x)h(x) , y f 0 (x) = (gh)0 (x) = g 0 (x)h(x) + g(x)h0 (x) = 2x · x + x2 · 1 = 3x2 .
En general, f (x) = xn es derivable en IR con f 0 (x) = nxn−1 y los polinomios son derivables en IR .
x2 −1 (2x)(x)−(x2 −1)(1) x2 +1
? f (x) = x , cociente de derivables, es derivable en su dominio y f 0 (x) = x2 = x2 . 4

Regla de la cadena 227.- Sea f derivable en x0 y g derivable en f (x0 ) , entonces la función compuesta g ◦ f
es derivable en x0 y además: ³ ´
(g ◦ f )0 (x0 ) = g 0 f (x0 ) f 0 (x0 ). .

Ejemplo f (x) = xα es derivable en (0, +∞) , pues f (x) = xα = eα ln(x) donde g(x) = ex y h(x) = α ln x
son derivables en sus dominios. Además, f 0 (x) = g 0 (h(x))h0 (x) = eα ln x (α x1 ) = xα αx = αxα−1 . 4

Prof: José Antonio Abia Vian I.T.I. en Electricidad

103 – Matemáticas I : Cálculo diferencial en IR 10.1 Derivada de una función en un punto

10.1.1 Aplicaciones de la derivada

Regla simple de L’Hôpital 228.- Si f (x0 ) = g(x0 ) = 0 y f y g son derivables en x0 con g 0 (x0 ) 6= 0.
f (x) f 0 (x0 )
Entonces, lı́m = 0 .
x→x0 g(x) g (x0 )
Demostración:
Por ser f y g derivables en x0 , y f (x0 ) = g(x0 ) = 0, se tiene
f (x)−f (x0 )
f (x)−f (x0 ) lı́m
f (x) f (x) − f (x0 ) x−x0 x→x0 x−x0 f 0 (x0 )
lı́m = lı́m = lı́m = =
x→x0 g(x) x→x0 g(x) − g(x0 ) x→x0 g(x)−g(x0 )
lı́m g(x)−g(x0 ) g 0 (x0 )
x−x0 x→x0 x−x0

sen x
Ejemplo lı́m x = 1 pues f (x) = sen x y g(x) = x, verifican las condiciones del resultado, f (0) = g(0) = 0 ,
x→0
0 0 sen x cos(0)
f (0) = cos(0) y g (0) = 1 . Luego lı́m x = 1 =1 4
x→0

ln x
Ejemplo Calcular el valor del lı́mite lı́m 2 .
x→1 cos(πx)+e1−x
1
La función f (x) = ln x verifica que f (1) = 0 y derivable en 1 con f 0 (x) = x y f 0 (1) = 1.
2
La función g(x) = cos(πx) + e1−x verifica que g(1) = cos(π) + e0 = −1 + 1 = 0 y derivable en 1 con
2
g 0 (x) = −π sen(πx) + e1−x (−2x) y g 0 (1) = −π sen(π) + e0 (−2) = −2 6= 0 .
ln x 1
Luego lı́m cos(πx)+e 1−x2
= −2 4
x→1

Nota: La derivación es una potente herramienta para el cálculo de lı́mites, no solo por el resultado anterior
sino por la más útil Regla General de L’Hôpital 238 y los polinomios de Taylor, que veremos más adelante.

10.1.1.1 Crecimiento de una función en un punto. Extremos locales

El significado de la derivada como lo que crece la función cerca del punto, queda de manifiento con el siguiente
resultado:
Teorema 229.- Sea f : (a, b) −→ IR derivable en el punto x0 ∈ (a, b) . Entonces, si f 0 (x0 ) > 0 (resp. f 0 (x0 ) <
0 ) la función f es estrictamente creciente (resp. decreciente) en x0 .
Demostración:
f (x)−f (x0 ) f (x)−f (x0 )
Si f 0 (x0 ) > 0, como f 0 (x0 ) = lı́m x−x0 , se tiene que x−x0 > 0 para los x cercanos a x0 . Entonces
x→x0

? si x0 < x , como x − x0 > 0, necesariamente f (x) − f (x0 ) > 0 de donde f (x0 ) < f (x)
? y si x < x0 , es x − x0 < 0 y debe ser f (x) − f (x0 ) < 0 de donde f (x) < f (x0 )

Análogamente, para f 0 (x0 ) < 0 .

Definición 230.- Sea f : (a, b) −→ IR , se dice que f alcanza un máximo local en el punto x0 ∈ (a, b) (o que
f (x0 ) es un máximo local de f ) si f (x) ≤ f (x0 ) para todos los x de algún entorno E(x0 , δ) de x0 .
Se dice f alcanza un mı́nimo local en x0 si f (x0 ) ≤ f (x) para todos los x del entorno.
Nota: Diremos extremo local para referirnos indistintamente a un máximo o un mı́nimo local.

Proposición 231.- Sea f : [a, b] −→ IR continua y c ∈ (a, b). Si f es decreciente en cada x ∈ [a, c) y creciente
en cada x ∈ (c, b], entonces f (c) es un mı́nimo local de f .
Si f es creciente en cada x ∈ [a, c) y decreciente en cada x ∈ (c, b], f (c) es un máximo local de f .
Demostración:
En efecto, en el primer caso, por ser f continua en [a, b] existe el mı́nimo de f en el conjunto, pero no se puede
alcanzar en un punto de [a, c) ya que todos los puntos son decrecientes (el valor de f en el punto es mayor que
los cercanos de su derecha); y no puede alcanzarse en (c, b] ya que todos los puntos son crecientes (el valor de f

Prof: José Antonio Abia Vian I.T.I. en Electricidad

104 – Matemáticas I : Cálculo diferencial en IR 10.1 Derivada de una función en un punto

en el punto es mayor que los cercanos de su izquierda). Luego necesariamente, el mı́nimo tiene que alcanzarse
en c . Análogamente, para el caso del máximo.

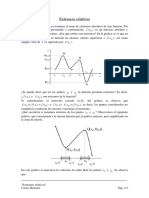
Ejemplo La función f (x) = |x| presenta un mı́nimo local en 0, pues es continua en

IR (luego en cualquier intervalo cerrado como [−1, 1] ), decreciente a la izquierda de 0
r
( f (x) = −x) y creciente a la derecha ( f (x) = x ). 4

Nota: La hipótesis de continuidad de la función es imprescindible para

asegurar el resultado. En la figura aneja pueden observarse distintas b b
situaciones en las que sin continuidad no hay los extremos esperados: r r
en los dos primeros casos la función no alcanza el máximo esperado y no b
hay extremo local; en el tercero, no se tiene el máximo esperado aunque
sı́ un extremo ya que se alcanza un mı́nimo local en el punto.
Con la continuidad, si f es creciente (o decreciente) en los puntos
a derecha e izquierda de c, también se garantiza la no existencia de
b r
extremo. Pero sin continuidad, a pesar de ser creciente antes del punto
y creciente despues del punto puede existir extremo, como en la cuarta r b
situación de la figura donde tenemos un máximo local.

Corolario 232.- Sea f : [a, b] −→ IR continua en [a,b] y derivable en (a, b). Si f 0 (x) < 0 (resp. f 0 (x) > 0 ) para
cada x ∈ (a, c) y f 0 (x) > 0 (resp. f 0 (x) < 0) en cada x ∈ (c, b), la función f alcanza en c un mı́nimo local
(resp. máximo local).

2
Ejemplo La función f (x) = e−x , continua y derivable en IR , presenta un máximo local en 0, pues su
2
derivada f 0 (x) = e−x (−2x) es positiva si x < 0 y negativa si x > 0. 4

Teorema 233 (Condición necesaria de extremo).- Sea f : (a, b) −→ IR . Si f es derivable en el punto

c ∈ (a, b) y f alcanza un extremo local en c, entonces f 0 (c) = 0 .
Demostración:
f (x)−f (c) f (x)−f (c) f (x)−f (c)
Si f es derivable en c , existe f 0 (c) = lı́m x−c = x→c
lı́m x−c = x→c
lı́m x−c . Entonces
x→c
x<c x>c

? si f (c) es un máximo local, se verifica que f (x) − f (c) ≤ 0 para los x cercanos a c, luego

f (x) − f (c) ³ ≤ 0 ´ f (x) − f (c) ³ ≤ 0 ´

f 0 (c) = x→c
lı́m = ≥0 y f 0 (c) = x→c
lı́m = ≤0 =⇒ f 0 (c) = 0
x<c
x−c ≤0 x>c
x−c ≥0

? Análogamente, si f (c) es mı́nimo local, f (x) − f (c) ≥ 0 , luego

f (x) − f (c) f (x) − f (c)

f 0 (c) = x→c
lı́m ≤0 y f 0 (c) = x→c
lı́m ≥0 =⇒ f 0 (c) = 0
x<c
x−c x>c
x−c

2
Ejemplo La función f (x) = e−x del ejemplo anterior, es derivable en 0 y presenta un máximo local en 0.
2
Y ciertamente se verifica que f 0 (0) = e−0 (−2 · 0) = 0 . 4

La condición anterior es sólo una condición necesaria, bajo la hipótesis de derivación, pero no es suficiente
para asegurar la existencia de extremo. Es decir, de los puntos donde la función sea derivable puede alcanzarse
extremo únicamente en aquellos donde la derivada se anule, pero también puede no alcanzarse extremo en
ellos. Son, de entre los puntos derivables, los únicos puntos candidados a albergar extremo.
En consecuencia, para encontar los extremos locales de una función, basta con buscarlos entre los puntos
donde sea derivable, con derivada cero, y los puntos donde la función no sea derivable.

Ejemplo La función f (x) = x3 es derivable en IR y f 0 (x) = 3x2 se anula en x = 0, pero no tiene extremo
local en el punto.

Prof: José Antonio Abia Vian I.T.I. en Electricidad

105 – Matemáticas I : Cálculo diferencial en IR 10.2 Teoremas de derivación

3x4 −8x3
Ejemplo La función f (x) = 16 es continua en [−1, 3] y derivable en r
0 3x2 (x−2) 0
(−1, 3); su derivada en (−1, 3) es f (x) = y se anula ( f (x) = 0)
4
en los puntos x = 0 y x = 2 . Entonces los únicos puntos “candidatos” r
a albergar un extremo local son x = 0 y x = 2 (donde existe la derivada
y se anula), pero también los puntos x = −1 y x = 3 donde la función r
no es derivable (por ser extremos del intervalo de definición). De hecho,
el los extremos del intervalo se alcanza extremo local ( f (−1) y f (3) son
máximos locales) y también en el punto interior x = 2 ( f (2) es mı́nimo r
local); mientras que el otro “candidato” x = 0 no alberga extremo. 4

10.2 Teoremas de derivación

Los tres teoremas siguientes son básicos para pasar los resultados de derivación sobre puntos a todo un intervalo,
lo que nos servirá además para contruir mejores herramientas de trabajo.
Teorema de Rolle 234.- Sea f : [a, b] −→ IR tal que f es continua en [a, b] y derivable en (a, b) y además
f (a) = f (b), entonces ∃ c ∈ (a, b) tal que f 0 (c) = 0.
Demostración:
Por ser f continua en [a, b] , el Teorema de Weierstrass (222) garantiza que se alcanzan el máximo y el mı́nimo
en el conjunto. Entonces,
? si se alcanza uno de los extremos en algún c ∈ (a, b) , por ser f derivable en (a, b) , se cumple que f 0 (c) = 0
? si los extremos se alcanzan en a y b , por ser f (a) = f (b) , el máximo y el mı́nimo deben coincidir, por lo
que la función es constante en [a, b] y f 0 (c) = 0 para todo c ∈ (a, b) .

Ejemplo La función polinómica f (x) = x4 − 4x2 se anula en x = 0 y x = 2, luego f (0) = 0 = f (2) y es

continua y derivable en [0, 2]. Entonces, el polinomio f 0 (x) = 4x3 − 8x tiene alguna raı́z entre 0 y 2 . 4

Nota: Si la función no es constante, el teorema de Rolle tiene otra lectura: se asegura la existencia de al menos
un extremo en el intervalo. Geométricamente, el teorema de Rolle significa que existe un punto con tangente
horizontal.
El teorema siguiente, conocido como de los f 0 (c) =
f (b)−f (a)
b−a
incrementos finitos o del valor medio de La- 0
f (c) = 0 r
grange, generaliza el Teorema de Rolle. Y, en r
f (b) q
sentido geométrico, significa que hay un punto q q q
f (a) = f (b) f (a)
cuya recta tangente tiene la misma pendiente
que la cuerda que une los puntos extremos de a c b a c b
la gráfica f (b)−f
b−a
(a)
= f 0
(c) . Teorema de Rolle Teorema de Lagrange

Teorema del valor medio de Lagrange 235.- Sea f : [a, b] −→ IR tal que f es continua en [a, b] y derivable
en (a, b), entonces ∃c ∈ (a, b) tal que:

f (b) − f (a) = f 0 (c)(b − a)

Demostración:
f (b)−f (a)
Como a 6= b, podemos escribir f 0 (c) = b−a , es decir, buscamos un c ∈ (a, b) tal que f 0 (c) sea la pendiente
de la cuerda entre los puntos (a, f (a)) y (b, f (b)) que tiene por ecuación y = f (a) + f (b)−f
b−a
(a)
(x − a).
¡ f (b)−f (a) ¢
Consideremos entonces la función g(x) = f (x) − f (a) + b−a (x − a) (la función menos la cuerda)
para llevar el problema a las condiciones del teorema de Rolle. En efecto, g: [a, b] −→ IR es continua en [a, b] y
¡ ¢
derivable en (a, b) por ser suma de continuas y derivables, además, g(a) = f (a) − f (a) + f (b)−f b−a
(a)
(a − a) = 0
¡ ¢
y g(b) = f (b) − f (a) + f (b)−f
b−a
(a)
(b − a) = 0 .
Entonces, existe c ∈ (a, b) tal que g 0 (c) = 0; y como g 0 (x) = f 0 (x) − f (b)−f
b−a
(a)
, se tiene la igualdad propuesta
f (b)−f (a)
ya que 0 = f 0 (c) − b−a .

Prof: José Antonio Abia Vian I.T.I. en Electricidad

106 – Matemáticas I : Cálculo diferencial en IR 10.2 Teoremas de derivación

El último de los teoremas y más general es el teorema de Cauchy. Aunque gráficamente no tiene un significado
claro, es muy útil para la extensión de la teorı́a:
Teorema del valor medio de Cauchy 236.- Sean f y g funciones continuas en [a, b] y derivables en (a, b).
Si g 0 (x) 6= 0 , ∀ x ∈ (a, b) , entonces ∃ c ∈ (a, b) tal que:

f (b) − f (a) f 0 (c)

= 0 .
g(b) − g(a) g (c)

Con los teoremas anteriores y la derivación, ya se puede asegurar la monotonı́a por intervalos:
Proposición 237.- Si f es un función continua en [a, b] y derivable en (a, b) y f 0 (x) > 0, ∀ x ∈ (a, b), entonces
f es estrictamente creciente en [a, b].
Si f es una función continua en [a, b] y derivable en (a, b) y f 0 (x) < 0, ∀ x ∈ (a, b) , entonces f es
estrictamente decreciente en [a, b].
Demostración:
Para cualesquiera x1 , x2 ∈ [a, b], con x1 < x2 , consideremos el intervalo [x1 , x2 ]. Podemos aplicar el teorema
del valor medio de Lagrange en este intervalo, luego ∃ c ∈ (x1 , x2 ) tal que f (x2 ) − f (x1 ) = f 0 (c)(x2 − x1 ).
Entonces,
? si f 0 > 0 en (a, b), también f 0 (c) > 0 y se tiene que f (x2 ) − f (x1 ) = f 0 (c)(x2 − x1 ) > 0 por lo que
f (x1 ) < f (x2 ) y, en consecuencia, f es estrictamente creciente en [a, b].
? si f 0 < 0 en (a, b), también f 0 (c) < 0 y se tiene que f (x2 ) − f (x1 ) = f 0 (c)(x2 − x1 ) < 0 por lo que
f (x1 ) > f (x2 ) y, en consecuencia, f es estrictamente decreciente en [a, b].

Y también podemos obtener el resultado de la Regla General de L’Hôpital para el cálculo de lı́mites:
Regla General de L’Hopital 238.- Sean f y g funciones derivables en un entorno reducido de x0 , E ∗ (x0 , δ),
con g(x) 6= 0 y g 0 (x) 6= 0, ∀ x ∈ E ∗ (x0 , δ) y lı́m f (x) = 0 = lı́m g(x). Entonces,
x→x0 x→x0
0
f 0 (x)
si existe lı́m fg0 (x)
(x)
se cumple que lı́mf (x)
= lı́m 0 . .
x→x0 x→x0 g(x) x→x0 g (x)

Nota: Esta regla es también válida en los casos en que x0 sea +∞ ó −∞ y cuando lı́m f (x) = +∞ ó −∞
x→x0
y lı́m g(x) = +∞ ó −∞, (también en este caso x0 puede ser +∞ ó −∞ ) sin más que traducir las hipótesis
x→x0
de f y g a entornos de +∞ ó −∞.

sen(x)−x
Ejemplo Calcular el lı́m x3 . Las funciones f (x) = sen(x) − x y g(x) = x3 son derivables en IR ,
x→0
con f (0) = 0 = g(0); y sus derivadas son f 0 (x) = cos(x) − 1 y g 0 (x) = 3x2 . Entonces, por L’Hôpital, el lı́mite
inicial existe si existe él del cociente de las derivadas, por lo que hemos trasladado el problema al cálculo de un
nuevo lı́mite lı́m cos(x)−1
3x2 . Como también es indeterminado y las derivadas son derivables, podemos aplicar de
x→0
nuevo L’Hôpital para resolver este lı́mite. Sucesivamente, tendremos que
sen(x) − x cos(x) − 1 − sen(x) −1 sen(x) −1
lı́m 3
= lı́m 2
= lı́m = lı́m =
x→0 x x→0 3x x→0 6x 6 x→0 x 6
La existencia del último lı́mite garantiza la cadena de igualdades. 4

tg( π
2 −x)
Ejemplo Calcular lı́m ln x .
x→0+
+∞ tg( π −x)
Como las funciones del cociente son derivables cerca de 0+ , y ln2 x → −∞ , aplicando l’Hôpital
−1
π
tg( 2 −x) cos 2 ( π −x) ¡ − ¢
lı́m ln x = lı́m 1
2
= lı́m cos2−x 0 −1 −1
( π −x) = 0+ = lı́m 2 cos( π −x)(− sen( π −x))(−1) = ( 0+ ) = −∞ 4
x→0 + x→0+ +
x x→0 2 x→0+ 2 2

2 2
Ejemplo Sabemos que lı́m x2 −x = 1 , y usando l’Hôpital lı́m x2 −x = lı́m 2x−1
= lı́m 2
=1 4
x→+∞ x +3x x→+∞ x +3x x→+∞ 2x+3 x→+∞ 2

Añadamos un resultado que puede parecer irrelevante, pero que resulta de utilidad para las funciones defi-
nidas a trozos:

Prof: José Antonio Abia Vian I.T.I. en Electricidad

107 – Matemáticas I : Cálculo diferencial en IR 10.2 Teoremas de derivación

Proposición 239.- Sea f : (a, b) −→ IR tal que f es continua en x0 ∈ (a, b), f es derivable en un entorno
reducido de x0 , y existen los lı́m+ f 0 (x) y lı́m− f 0 (x) . Entonces:
x→x0 x→x0
f es de derivable en x0 si y sólo si lı́m+ f 0 (x) = lı́m− f 0 (x).
x→x0 x→x0

Demostración:
Por ser f continua en x0 , f (x) → f (x0 ) cuando x → x0 y, por ser derivable, puede aplicarse la Regla de
L’Hôpital para obtener las igualdades de lı́mites siguientes:

f (x) − f (x0 ) f 0 (x) f (x) − f (x0 ) f 0 (x)

lı́m+ = lı́m+ = lı́m+ f 0 (x) lı́m− = lı́m− = lı́m− f 0 (x)
x→x0 x − x0 x→x0 1 x→x0 x→x0 x − x0 x→x0 1 x→x0

f (x)−f (x0 ) f (x)−f (x0 )

Entonces, si f es derivable en x0 , f 0 (x0 ) = lı́m− x−x0 = lı́m+ x−x0 y lı́m+ f 0 (x) = lı́m− f 0 (x).
x→x0 x→x0 x→x0 x→x0
f (x)−f (x0 )
0
Recı́procamente, si lı́m f (x) = lı́m f (x), entonces lı́m 0
x−x0 = lı́m f (x)−f
x−x0
(x0 )
y existe el lı́mite
+
x→x0 x→x−
0 x→x−
0 x→x+ 0
global, por lo que f es derivable en x0 y f 0 (x0 ) = lı́m+ f (x) = lı́m− f (x) . 0 0
x→x0 x→x0

½
x, si x ≥ 0
Ejemplos ? La función f (x) = |x| = no es derivable en x = 0. En efecto, es continua en
−x, si x < 0
x = 0 y derivable en IR − {0} , y como lı́m+ f 0 (x) = lı́m+ 1 = 1 6= lı́m− f 0 (x) = lı́m− −1 = −1 , la función
x→0 x→0 x→0 x→0
no es derivable en el punto.
½
x2 , si x ≥ 0
? La función f (x) = es derivable en x = 0. En efecto, es continua en x = 0 y derivable
−x2 , si x < 0
en IR − {0}, y como lı́m+ f (x) = lı́m+ 2x = 0 = lı́m− f 0 (x) = lı́m− −2x = 0, la función es derivable en
0
x→0 x→0 x→0 x→0
el punto y f 0 (0) = 0. 4

10.2.1 Teorema de la función inversa

El siguiente teorema garantiza de modo sencillo la existencia de función inversa en un conjunto y procura un
método para obtener las derivadas de la inversa aunque no conozcamos su expresión.
0
Teorema de la función inversa 240.- Sea f : [a, b] −→ IR continua en [a, b] y derivable
¡ ¢en (a,1 b), con f > 0 ó
0 −1 0
f < 0 en (a, b) . Entonces f admite función inversa derivable en (a, b) y (f ) f (x) = f 0 (x) . .

Corolario 241.- Si f es estrictamente creciente (resp. estrictamente decreciente), su inversa f −1 es estricta-

mente creciente (resp. estrictamente decreciente)
Demostración:
¡ ¢ 1
Como (f −1 )0 f (x) = f 0 (x) , su signo es el mismo que el de f 0 .

Corolario 242.- Si f 0 es continua, entonces la derivada de la inversa es también continua.

Ejemplo La función f (x) = tg x es continua y derivable en (− π2 , π2 ) , con f 0 (x) = 1 + tg2 x que es mayor que
cero en cada punto. Luego f es estrictamente creciente en el intervalo y su función inversa arctg: IR −→ (− π2 , π2 )
1
es también estrictamente creciente y (f −1 )0 (tg(x)) = 1+tg 2 x luego haciendo y = tg x , se obtiene que

1
(f −1 )0 (y) = (arctg y)0 = 4
1 + y2

Ejemplo La función f (x) = sh(x) es continua y derivable en IR , con f 0 (c) = ch(x) que es continua y mayor
que cero en el conjunto. Luego admite inversa en IR y su función inversa argsh: IR −→ IR tiene también derivada
1
continua. Como (f −1 )0 (sh(x)) = ch(x) haciendo y = sh(x) y usando que ch2 x − sh2 x = 1, se tiene

1
(f −1 )0 (y) = (argsh y)0 = p 4
1 + y2

Prof: José Antonio Abia Vian I.T.I. en Electricidad

108 – Matemáticas I : Cálculo diferencial en IR 10.2 Teoremas de derivación

Inversas de las demás funciones trigonométricas e hiperbólicas

f (x) = sen x tiene por inversa en [− π2 , π2 ] a arcsen: [−1, 1] −→ [− π2 , π2 ] y (arcsen y)0 = √ 1
1−y 2

f (x) = cos x tiene por inversa en [0, π] a arccos: [−1, 1] −→ [0, π] y (arccos y)0 = √−1
1−y 2
1
f (x) = ch x tiene por inversa en [0, +∞) a argch: [1, +∞) −→ [0, +∞) y (argch y)0 = √
y 2 −1
1
f (x) = th x tiene por inversa en IR a argth: (−1, 1) −→ IR y (argth y)0 = 1−y 2

10.2.2 Representación gráfica de funciones (1)

A lo largo de este tema (y también en el anterior) hemos obtenido resultados sobre el comportamiento de la
función: continuidad, monotonı́a, extremos, . . . . Resultados que también se reflejan en la gráfica de la función,
y que vamos a utilizar, para realizar un esbozo de la misma. La representación gráfica será más completa tras
el tema siguiente sobre las derivadas de órdenes superiores.

10.2.2.1 Monotonı́a y extremos locales

Basta para ello reunir algunos de los resultados ya obtenidos, en particular: uso del signo de la derivada para
el crecimiento de la función, la condición necesaria de extremos locales, la condición suficiente de extremo que
se da en la Proposición 231.
Para el estudio del signo de la función derivada, si esta es continua, puede resultar útil el Teorema de Bolzano.
Si f 0 (c) = 0 y f 0 (d) = 0 , f 0 continua en [c, d] y no se anula en ningún otro punto, el signo de
f 0 (x) es el mismo para todos los x ∈ (c, d).
En efecto, si dos puntos de (c, d), x1 y x2 , con x1 < x2 , verifican que f 0 tiene signos distintos, por ser
continua, tendrı́a que existir un punto x0 ∈ (x1 , x2 ) en el que f 0 (x0 ) = 0 en contra de que no se anula en
ningún punto más del conjunto. Luego todos tienen el mismo signo y para conocerlo basta con calcularlo en
uno de los puntos.

3x4 −8x3 r
Ejemplo La función f (x) = 16 es continua en [−1, 3] y derivable en
2
(−1, 3); su derivada en (−1, 3) es f (x) = 3x (x−2)
0
4 y se anula únicamente
en x = 0 y x = 2 . Como la función derivada f 0 (x) = 34 x2 (x − 2) es continua r
en (−1, 3) y en (−1, 0] sólo se anula en 0 , tiene el mismo signo en todos los
puntos de (-1,0); como f 0 ( −1 −15 r
2 ) = 32 < 0 en (−1, 0) es siempre negativa y
la función f es decreciente en (−1, 0) .
f 0 (x) es continua en [0, 2] y sólo se anula en los extremos, luego tiene el r
mismo signo en (0, 2). Como f 0 (1) = −3 4 < 0 es siempre negativa y f es
decreciente en (0, 2).
f 0 (x) es continua en [2, 3) y sólo se anula en 2, luego tiene el mismo signo en (2, 3). Como f 0 ( 52 ) = 75
32 > 0 es
siempre positiva y f es creciente en (2, 3) .
Los únicos puntos “candidatos” a albergar un extremo local son x = 0 y x = 2 (donde existe la derivada y
se anula), y los puntos x = −1 y x = 3 donde la función no es derivable por ser extremos del dominio.
Como f es continua en −1 y es decreciente en (−1, 0) , f (−1) es un máximo local. Como f es continua
en 0 y es decreciente en (−1, 0) y decreciente en (0, 2) , f (0) no es un extremo. Como f es continua en 2 y es
decreciente en (0, 2) y creciente en (2, 3), f (2) es un mı́nimo local. Como f es continua en 3 y es creciente en
(2, 3) , f (3) es un máximo local. 4

10.2.2.2 Concavidad y convexidad

Hemos visto en la condición necesaria de extremo local cómo, cuando es derivable, la derivada en el punto es
cero; o lo que es lo mismo, la recta tangente a la gráfica en el punto es horizontal. Si el extremo es un máximo,
para valores cercanos al punto los valores de la función son menores que el máximo local luego, gráficamente,
los puntos de la gráfica están por debajo de la recta tangente; y si es un mı́nimo los puntos de la gráfica están
por encima de la recta tangente. Pero, también eso puede ocurre en cualquier otro punto (ver la gráfica que
ilustra los teoremas de Rolle y del valor medio de Lagrange en pág 105) y nos lleva a las definiciones de función
cóncava y convexa.

Prof: José Antonio Abia Vian I.T.I. en Electricidad

 109 – Matemáticas I : Cálculo diferencial en IR 10.3 Ejercicios

Aunque pueden darse definiciones para las que no es necesaria la derivación (mejores y menos restrictivas que
éstas), las que damos a continuación son sencillas de introducir y más que suficientes para el uso que haremos
de los conceptos, pero también incorporann herramientas para una fácil manipulación.
Definición 243.- Diremos que una función f : (a, b) −→ IR , derivable en x0 ∈ (a, b) es convexa en el punto
x0 si f (x) ≤ f (x0 ) + f 0 (x0 )(x − x0 ) para los x de algún entorno de x0 .
Diremos que es cóncava en x0 si f (x) ≥ f (x0 ) + f 0 (x0 )(x − x0 ) para los x de algún entorno de x0 .
Diremos que es cóncava o convexa es un intervalo si lo es en cada punto.
Un punto de continuidad se dice de inflexión si la función cambia de concavidad en él.

Nota: En otras palabras, diremos que es convexa (cóncava) en x0 si, cerca de x0 , la gráfica de la función está
por debajo (encima) de la recta tangente en el punto. Con los comentarios hechos en la introducción de este
apartado, en los máximos donde la función sea derivable la función es convexa y en los mı́nimos cóncava.
Ejemplo La función f (x) = x2 ¡es cóncava en cada punto ¢ de IR . Como es derivable en cada punto x = a y
f 0 (x) = 2x , se cumple que f (x) − f (a) + f 0 (a)(x − a) = x2 − a2 − 2a(x − a) = x2 − 2ax + a2 = (x − a)2 ≥ 0
para todo x , luego f (x) ≥ f (a) + f 0 (a)(x − a) y es cóncava en cada punto.
Ejemplo La función f (x) = x2 (x − 3) , es convexa en x = 0, cóncava en x = 3 y presenta un punto de
inflexión en x = 1 .
En efecto, consideremos la función ga (x) = f (x) − (f (a) + f 0 (a)(x − a)) entonces, si ga (x) ≥ 0 en algún
entorno de a es cóncava en a, si ga (x) ≤ 0 en algún entorno de a es convexa en a y si ga (x) cambia de signo
en a es un punto de inflexión. Como ga (a) = 0 y es derivable (pues f lo es), veamos como se comporta cerca
de cada uno de los puntos indicados:

? En x = 0 , se tiene g00 (x) = 3x(x − 2), por lo que es positiva antes

de 0 y negativa depués (y g0 es creciente antes de 0 y decreciente
depués) luego g0 (x) ≤ g0 (0) = 0 en algún entorno de 0.
q q
? En x = 3 , se tiene g30 (x) = 3(x + 1)(x − 3) , por lo que es negativa
antes de 3 y positiva depués (y g3 es decreciente antes de 3 y
creciente depués) luego g3 (x) ≥ g3 (3) = 0 en algún entorno de 3.
q
? En x = 1 , se tiene g10 (x) = 3(x − 1)2 , por lo que es positiva antes
de 1 y también depués (y g1 es creciente antes de 1 y creciente
depués) luego g1 (x) ≤ g1 (1) = 0 para los x menores que 1 y
g1 (x) ≥ 0 para los x mayores que 1.

Luego es convexa en x = 0 , cóncava en x = 3 y tiene un punto de inflexión en x = 1 . 4

10.3 Ejercicios
10.107 Aplicar las reglas de derivación, para encontrar la expresión de f 0 en:
√ q q
a) f (x) = √x−1 b) f (x) = x−1
c) f (x) = √x−1
x+1 x+1 x+1
√
d) f (x) = ln x e) f (x) = ln(sen x) f) f (x) = (ln(2 − x2 ))−1
³ ´ −5
3
2+x
g) f (x) = arctg x2 h) f (x) = ln(arccos(tg(x2 ))) i) f (x) = √x−1
x+1

10.108 Encontar la expresión de las funciones derivadas, indicando el conjunto donde tienen validez:
√ 4
√1 x x x5
a) f (x) = x
b) f (x) = x2 +1 c) f (x) = (x+1)3
√ p
d) f (x) = x2 − 2x e) f (x) = ln |x| f) f (x) = − |x| − x

10.109 Hallar la recta tangente a las gráficas de las funciones siguientes en los puntos que se indican:
a) f (x) = x3 − x , en x = 0 y en x = 1.
1
b) f (x) = e x2 , en x = −1 y en x = 0.

Prof: José Antonio Abia Vian I.T.I. en Electricidad

 110 – Matemáticas I : Cálculo diferencial en IR 10.3 Ejercicios

√ √ +
c) f (x) = 2 − x2 , en x = 1 y en x = − 2 .

10.110 Probar que la parábola y = (x + 1)2 + 1 tiene recta tangente en todos sus puntos.
¿En qué puntos la recta tangente pasa por (0, 0) ?

10.111 Usar la regla de L’Hôpital, para calcular

x2 −4 x3 +23 7x3 +4x

a) lı́m
x 2 (2+x) b) lı́m c) lı́m 2 −2x3
x→−2 x→−2 x+2 x→0 3x−x
3 2
x+ex −1
d) lı́m 7x 2+4x 3 e) lı́m ln(cos
x2
x)
f) lı́m senarctg
x→∞ 3x−x −2x x→0 x→0 x
2
g) lı́m ln(x ) h) cos x
lı́m 2x−π i) lı́m (x + 1)( π2 − arctg(2x))
x→1 x−1 x→ π 2
x→∞
x
j) lı́m xe 6 k) lı́m xα ln |x| α ∈ IR l) lı́m lnαx α ∈ IR
x→∞ x→0 x→∞ x
³ ´ −1
1 1
m) lı́m ln x − x−1 n) lı́m xsen x o) lı́m (x2 + 1) x2
x→1 x→0+ x→∞

10.112 Estudiar la derivabilidad y obtener las derivadas, de las funciones del ejercicio 9.101.

10.113 Obtener las ası́ntotas de las funciones del ejercicio 9.101.

½ 1+4x
arctg 4x2 , si x 6= 0
10.114 Estudiar la continuidad y derivabilidad de la función f (x) = π , e indicar sus inter-
2, si x = 0
valos de crecimiento y decrecimiento. ¿Tiene ası́ntotas?
10.115 Para las funciones f , g y h del ejercicio 9.103:
a) Estudiar su derivabilidad en los puntos del dominio.
b) Dar la expresión de las funciones derivadas.
c) Obtener los intervalos de monotonı́a.
d) Estudiar la existencia de extremos locales.
e) Estudiar la existencia de ası́ntotas.
f) Estudiar la continuidad y derivabilidad de las funciones f 0 , g 0 y h0 .
√
x x
10.116 Hallar los extremos locales y globales de f (x) = 2
x +1 en [1, 3] y en [0, +∞).

10.117 Estudiar la monotonı́a de f (x) = x − sen x en [0, π] y deducir de ello que x ≥ sen x en [0, π].

10.118 Probar que:

a) Si f es una función estrictamente creciente, entonces
f ◦ g alcanza un máximo/mı́nimo en a ⇐⇒ h alcanza un máximo/mı́nimo en a
b) Si f es una función estrictamente decreciente, entonces
f ◦ g alcanza un máximo/mı́nimo en a ⇐⇒ g alcanza un mı́nimo/máximo en a

10.119 Usar los resultados del ejercicio 10.118, para encontrar los extremos locales de las funciones
x+1
1
a) f (x) = e x2 +3 b) f (x) = √
(x2 −5)2 +x2

10.120 Si f es par y alcanza un extremo en x = a, ¿alcanzará también un extremo en x = −a?

¿Que ocurrirá si f es impar? ¿Y si es periódica de periodo T ?
10.121 Problema: Con una cuerda atamos una vaca al exterior de un edificio de planta cuadrada situado en el
centro de un prado. Si la longitud de la cuerda es la misma que el lado del edificio, ¿en qué punto debemos
atar la vaca para que tenga la mayor área posible de pasto? ¿y la menor?
Modelado del problema: Representamos el edificio por un cuadrado de lado L , por ejemplo él de vértices
(0, 0), (L, 0) , (L, L) y (0, L) .
Como el edificio es cuadrado, ocurre lo mismo en cada lado, por lo que basta estudiar uno de los lados,
por ejemplo el lado inferior (el segmento {(x, 0) : x ∈ [0, L]} ).

Prof: José Antonio Abia Vian I.T.I. en Electricidad

 111 – Matemáticas I : Cálculo diferencial en IR 10.3 Ejercicios

Luego, para cada x ∈ [0, L], debemos encontrar un función f que asigne a cada x el área buscado, es
decir, tal que f (x) = área-abarcado-atando-en-x .
La solución del problema se obtiene encontrando los puntos donde de alcancen el máximo y el mı́nimo
global de f en el intervalo [0, L] .

a) Resolver el problema planteado.

b) Repetir el problema para una cuerda de longitud la mitad del perı́metro del edificio.

10.122 Descomponer 100 en dos sumandos tales que el cuádruplo del primero más el cuadrado del segundo sea
mı́nimo.
10.123 Hallar dos números cuya suma sea a, de modo que la suma de la cuarta potencia de uno, más el cuadrado
del otro, sea máxima.
10.124 Entre todos los rectángulos de área 50, ¿cuál es el de perı́metro mı́nimo? ¿y máximo?

10.125 Sean los triángulos rectángulos que tienen la suma de los catetos constante (e igual a k ). ¿Cuál de ellos
tiene área máxima?

10.126 Dado un triángulo isósceles de base 8 cm y altura 5 cm, hallar las dimensiones de un rectángulo inscrito
en él de área máxima.
10.127 Un prisma de 15 cm de altura tiene como base un triángulo rectángulo de hipotenusa igual a 10 cm.
Calcular las longitudes de los catetos para que el volumen sea máximo.
10.128 De entre todos los cilindros con volumen 100π cm 3 , escoger el de área lateral máxima. ¿Cuál es el de
área total máxima?
10.129 Hallar las distancias mı́nima y máxima del punto (1, 1) a la circunferencia (x − 2)2 + (y − 2)2 = 9.

10.130 Hallar, las dimensiones del cilindro de volumen máximo inscrito en una esfera de radio R

10.131 Hallar, las dimensiones del cilindro de área total máxima inscrito en una esfera de radio R

10.132 Un pescador en bote de remos se encuentra, mar adentro, a una distancia de 2 km. del punto más cercano
de una playa recta y desea llegar a otro punto de la playa a 6 km. del primero. Suponiendo que se puede
remar a una velocidad de 3 km/h. y caminar a 5 km/h, ¿qué trayectoria debe seguir para llegar a su
destino en el menor tiempo posible? Si tiene una lancha que viaja a 15 km/h, ¿qué trayectoria debe seguir
ahora?

10.133 Hay que cortar un hilo de longitud L en dos trozos. Con uno de ellos se forma un cı́rculo, y con el otro
un cuadrado. ¿Cómo hay que cortar el hilo para que la suma de las áreas sea máxima? ¿Y para que sea
mı́nima?.
10.134 Un camión ha de recorrer 300 kms en una carretera llana a una velocidad constante de x km/h. Las leyes
de circulación prescriben para la velocidad un máximo de 60 km/h y un mı́nimo de 30 km/h. Se supone
x2
que el carburante cuesta 3 duros/litro y que el consumo es de 10 + 120 litros por hora. El conductor cobra
10 duros por hora. Teniendo en cuenta que la empresa paga al conductor y el carburante, a qué velocidad
tendrá que viajar el camión para que el dinero desembolsado por la empresa sea mı́nimo.
10.135 Sea f (x) una función derivable en todo IR , cuya gráfica es simétrica respecto al eje OY .
a) Estudiar la paridad (simetrı́a) de f 0 (x).
b) Determinar, si es posible, f 0 (0).

10.136 Sea f una función de clase 1 (derivable con derivada continua) en la recta real IR . Supongamos que f
tiene exactamente un punto crı́tico x0 que es un mı́nimo local estricto de f . Demostrar que x0 también
es un mı́nimo absoluto para f .

Prof: José Antonio Abia Vian I.T.I. en Electricidad