Basics 1

8.4 The Normal Curve

The essential terms:

density scale
normal curve
standard normal curve
standardized score (z-score)

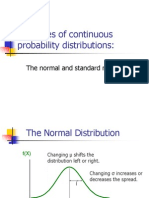
The normal curve is the familiar symmetric, bell shaped curve that's often used to approximate the
distribution of measurements in a population.
Example:

The distribution of the number of hours that college students sleep on a week night is
approximated by the normal curve displayed in the figure below. Characteristics of the model
were determined from data collected in a statistics class at Penn State University.

Probability Equals Area Under the Curve

The vertical axis in the drawing of the normal curve above is a density scale. When a density scale
is used, probability equals area under the curve.
Example:

file:///D|/RHO/stat200/normal2.htm (1 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

The proportion of college students who sleep between 5.5 and 8.5 hours is the area under the
normal curve between 5.5 and 8.5 hours, an area shown in the following figure.

Characteristics of the Normal Curve

Some important features of the normal curve are:

● The shape is a symmetric bell curve shape.

● Measurements relatively close to the mean are more probable than measurements relatively
far from the mean.
● The center of the distribution is the mean.

● The spread of the bell is determined by the standard deviation.

There actually are several probability distribution models that have these characteristics. The
normal curve is by far the most commonly used model with these features.

Notation for the Population Mean and Standard Deviation

The normal curve is a model for the distribution of measurements in a population.

● The symbol µ is used to represent the population mean.
● The symbol σ is used to represent the population standard deviation.

Page 2- The Standard Normal Curve

Standardized Scores

A standardized score, also called a z-score, measures how many standard deviations a value is
from the mean.

file:///D|/RHO/stat200/normal2.htm (2 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

A formula for calculating a standardized score is

Example:
Suppose that the mean pulse rate in a population is 75 beats per minute and the standard
deviation is 10.
● For a pulse rate of 85, the standardized score is 1 .
z = ( value - mean ) / s.d. = ( 85 - 75 ) / 10 = 1.

● For a pulse rate of 70, the z-score is - 0.5 .

z = ( value - mean ) / s.d. = ( 70 - 75 ) / 10 = - 0.5 .

Standardize to Solve Normal Curve Problems

Every normal curve problem can be solved by converting the problem to an equivalent question
about standardized scores.

Example:
Suppose that the distribution of pulse rates in a population is described by a normal curve with
a mean of 75 beats per minute and a standard deviation equal to 10.
The standardized score for a pulse rate of 85 is z = 1.
The proportion of the population that has a pulse rate less than 85 is also the proportion that
has a z-score less than 1.

The Standard Normal Curve

The standard normal curve is a normal curve model for z-scores. In this model, the mean is 0
and the standard deviation is 1
The standard normal curve is used to solve every normal curve problem, whether the problem is
about heights, IQs, hours of sleep, or any other variable.

Finding Areas Under the Standard Normal Curve

● The table on page 232 of the packet shows the area to the left of a z-score.

● Spreadsheet programs, like Excel, have commands that calculate normal curve areas.

file:///D|/RHO/stat200/normal2.htm (3 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

● Graphing calculators, like the TI-83, also have commands that can be used.

Solving Normal Curve Problems

We now demonstrate how to solve general normal curve problems. As an example, we use the
normal curve model for college students' hours of sleep on a week night that we described in 'The
Basics' section.
● The mean is µ = 7 hours
● The standard deviation is σ = 1.7 hours.

How to Find the Proportion Less Than a Value

To find the proportion of a population with a value less than a specified value:
1. Calculate a z-score for the specified value.
2. Determine the area to the left of the z-score.

Example
About what proportion of students sleep less than 5 hours on a week night? This will be the
area to the left of 5 hours.

The solution:
1. Calculate the standardized score for 5 hours of sleep. The formula is

file:///D|/RHO/stat200/normal2.htm (4 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

For 5 hours, z = ( 5 - 7 ) / 1.7 = -2 / 1.7 = -1.18

2. Use the table on page 232 to find the area to the left of -1.18.
The answer is about 0.12 (about 12% ). About 12% of college students sleep less than 5
hours on a week night.
Note: If the proportion sleeping less than 5 hours is 0.12 the proportion sleeping more than
5 hours is 1-0.12 = 0.88 .

How to Find the Proportion Greater Than a Value

To find the proportion of a population with a value greater than a specified value:
1. Calculate a z-score for the specified value.
2. Determine the area to the left of the z-score.
3. Area to the right = (1-area to the left).

Example
About what proportion of students sleep more than 10 hours on a week night? This is the area
to the right of 10 hours.

The solution:

file:///D|/RHO/stat200/normal2.htm (5 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

1. Calculate the z-score for 10 hours.

Z = ( 10 - 7 ) / 1.7 = 3 / 1.7 = 1.76
2. Find the area to the left of Z=-1.76. The answer is about 0.96. (Use p. 232).
3. Calculate (1-answer in step 2).
1 - 0.96 = 0.04 (about 4%). About 4% of college students sleep more than 10 hours
per night.

How to Find the Proportion in an Interval

To find the proportion of a population that falls in a specified interval:

1. Calculate a z-score for each end of the interval.
2. Find the area (probability) to the left of each z-score.
3. Calculate the difference between the two probabilities

On a week night, what percentage of students sleep between 5 and 10 hours? This is the area
between 5 hours and 10 hours.

The solution -
We learned information about 5 and 10 hours of sleep in the previous two solutions.
1. For 10 hours, z = 1.76. For 5 hours, z = -1.18.

2. To the left of z =1.76, the area is about 0.96.

file:///D|/RHO/stat200/normal2.htm (6 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

To the left of z =-1.18, the area is about 0.12.

3. The answer is 0.96 - 0.12 = 0.84. About 84% of college students sleep between 5 and
10 hours on a week night.

How to Find a Percentile

The term "percentile rank" refers to the area (probability) to the left of a value. For instance, we
found that the area to the left of 5 hours of sleep is 0.1190. This means that:
● the percentile rank for 5 hours is 0.1190 (about 12%)

● the 12th percentile is 5 hours

To find the value corresponding to a specified percentile rank:

1. Determine the z-score that has the given percentile rank.
2. Figure out what value has that z-score.

Example
What is the 98th percentile of the distribution of hours of sleep? The probability to the left of
the answer is 0.98.

The solution:
1. Find the z-score for which the area to the left is 0.98.
Look for 0.98 under Prob<=Z in the table on page 232.
● The value under Z Score is 2.05. The 98th percentile is 2.05 standard deviations above
the mean.
2. Determine the sleep value that has a z-score of 2.05.

file:///D|/RHO/stat200/normal2.htm (7 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

● 2.05 standard deviations is ( 2.05 )( 1.7 )

= 3.5 hours.
● 3.5 hours above the mean of 7 hours
= 10.5 hours.
The 98th percentile of the sleep distribution is 10.5 hours.

A formula to calculate the value that has a known z-score is

X=Zσ+µ
For z = 2.05 , x = (2.05) (1.7) + 7 = 3.5 + 7 = 10.5 hours.

The Empirical Rule and Outliers

The following three statements constitute the empirical rule.

1. About 68% of the values in a population described by a normal curve are within one
standard deviation of the mean.

2. About 95% of the values in a population described by a normal curve are within two
standard deviations of the mean.

3. About 99.7% of the values in a population described by a normal curve are within three
standard deviations of the mean.
The empirical rule is also called the 68 - 95 - 99.7% rule .

Example:
The number of hours that college students sleep on a week night is approximated by a normal
curve with a mean of 7 hours and a standard deviation of 1.7 hours.
● About 68% of college students sleep between 5.3 and 8.7 hours on a week night. The
calculation is 7 ± 1.7

● About 95% of college students sleep between 3.6 and 10.4 hours on a week night. The
calculation is 7 ± (2•1.7)

● About 99.7% of college students sleep between 1.9 and 12.1 hours in a week night. The
calculation is 7 ± (3•1.7)

When is a Value an Outlier?

There is no universally accepted criterion for declaring a point to be an outlier, but most data

file:///D|/RHO/stat200/normal2.htm (8 of 9) [3/14/2000 1:19:49 PM]

 Basics 1

analysts are suspicious when a data value's z-score is not between -3 and +3 .
The motivation for this guideline is that about 99.7% of the values in a population described by a
normal curve are within three standard deviations of the mean. In other words, nearly all z-scores
are between -3 and +3.

Example
In the Penn State sleep survey, one student's response was that he had slept 16 hours the
previous day.
Let's see where 16 hours falls in the normal curve model for sleep.
z = ( 16 - 7 ) / 1.7 = 9/1.7 = 5.29
This z-score is outside the range -3 to +3 so we call it an outlier.
We can also use the table on page 232 to find the probability to the left of z = 5.29. The closest
z-score in the table is z = 5. The probability to the left of this z-score is 0.9999997, or, in
percent terms, about 99.99997%.
In other words, 16 hours of sleep is around the 99.99997th percentile of the distribution. Quite
an accomplishment!

file:///D|/RHO/stat200/normal2.htm (9 of 9) [3/14/2000 1:19:49 PM]