Menachem Kojman and Saharon Shelah - Universal Abelian Groups
Diunggah oleh
JtyhmfDeskripsi Asli:
Judul Asli
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Menachem Kojman and Saharon Shelah - Universal Abelian Groups
Diunggah oleh
JtyhmfHak Cipta:
Format Tersedia
1
455 Universal Abelian Groups by Menachem Kojman and Saharon Shelah* ABSTRACT
6.10.2003
We examine the existence of universal elements in classes of innite abelian groups. The main method is using group invariants which are dened relative to club guessing sequences. We prove, for example: Theorem: For n 2, there is a purely universal separable p-group in n if, and only if, 20 n . 0 Introduction In this paper group will always mean innite abelian group, and cardinal and cardinality always refer to innite cardinals and innite cardinalities. Given a class of groups K and a cardinal we call a group G K universal for K in if |G| = and every H K with |H| is isomorphic to a subgroup of G. The objective of this paper is to examine the existence of universal groups in various well-known
modified:1996-03-19
classes of innite abelian groups. We also investigate the existence of purely universal groups for K in , namely groups G K with |G| = such that every H K with |H| is isomorphic to a pure subgroup of G. The main set theoretic tool we use is a club guessing sequence. This is a prediction principle which has enough power to control properties of an innite object which are
revision:1994-06-16
dened by looking at all possible enumerations of the object. Unlike the diamond and the square, two combinatorial principles which are already accepted as useful for the theory of innite abelian groups, club guessing sequences are proved to exist in ZFC. Therefore using club guessing sequences does not require any additional axioms beyond the usual * Partially supported by the United StatesIsrael Binational science foundation. Publication number 455 1
455
455
6.10.2003
axioms of ZFC. Club guessing sequences are particularly useful in proving theorems from negations of CH and GCH. The paper is organized as follows: in section 1 we dene group invariants relative to club guessing sequences, and show that the invariants are monotone in pure embeddings. In Section 2 we construct various groups with prescribed demands on their invariants. In section 3 these ideas are used to investigate the existence of universal groups for classes of torsion groups and classes of torsion free groups. It appears that cardinal arithmetic decides the question of existence of a universal group in many cardinals. For example: there is a purely universal separable p-group in n i n 20 for all n 2 (for n = 1 only the if part holds). This paper follows two other papers by the same authors, [KjSh 409] and [KjSh 447], in which the existence of universal linear orders, boolean algebras, and models of unstable and stable unsuperstable rst order theories were examined using the same method. All the abelian group theory one needs here, and more, is found in [Fu], whose system
modified:1996-03-19
of notation we adopt. An acquaintance with ordinals and cardinals is necessary, as well as familiarity with stationary sets and the closed unbounded lter. Knowledge of chapter II in [EM] is more than enough. Before getting on, we rst observe that in every innite cardinality there are universal groups which are divisible: 0.1 Theorem: In every cardinality there is a universal group, universal p-group (for
revision:1994-06-16
every prime p), universal torsion group and universal torsion-free group. Proof: These are, respectively, the direct sum of copies of the rational group Q together with copies of Z(p ) for every prime p; the direct sum of copies of Z(p ); the direct sum of copies of Z(p ) for every prime p; and the direct sum of copis of Q. The universality of these groups, each for its respective class, follows from the structure 2
455
455
6.10.2003
theorem for divisible groups and the fact that every group (p-group, torsion group, torsionfree group) is embeddable in a divisible group (p-group, torsion group, torsion-free group) of the same cardinality ([Fu] I, 23 and 24]) 1 The invariant of a group relative to the ideal id(C) A xed assumption in this section is that is a regular uncountable cardinal. We assume the reader is familiar with the basic properties of closed unbounded sets of , and with the denition and basic properties of stationary sets. 1.1 Denition: For a group G, nG = {ng : g G}. Two elements g, h G are ncongruent if g h nG. If g, h are n-congruent, we also say that h is an n-congruent of g. 1.2 Denition: (1) ([Fuch, p.113]) Let G be group. A subgroup H G is a pure subgroup, denoted by H pr G, if for all natural n, nH = nG H. (2) An embedding of groups h : H G is a pure embedding if its image h(H) is a pure
modified:1996-03-19
0.1
def
subgroup of G. 1.3 Denition: Suppose that is a regular uncountable cardinal and that G is a group of cardinality . A sequence G = G : < is called a -ltration of G i for all (1) G G+1 (2) G is of cardinality smaller than
revision:1994-06-16
(3) if is limit, then G = (4) G =
<
<
G .
Suppose G = G : < is a given ltration of a group G. Suppose c is a set of ordinals, and the increasing enumeration of c is i : i < i() . Let g G be an element. We dene a way in which g chooses a subset of c: 1.4 Denition: InvG (g, c) = {i c : g 3
n ((Gi +1
+ nG) (Gi + nG))}
455
455
6.10.2003
We call InvG (g, c) the invariant of the element g relative to the -ltration G and the set of indices c. Worded otherwise, InvG (g, c), is the subset of those indices i such that by increasing the group Gi to the larger group Gi+1 , an n-congruent for g is introduced for some n. As the denition of the invariant depends on a -ltration, one may think that the invariant does not deserve its name. Indeed, given a group G equipped with two respective -ltrations G and G , it is not necessarily true that for g G
(1)
InvG (g, c) = InvG (g, c)
The solution to this problem is working with a club guessing sequence C = c : S and the ideal id(C) associated to it. The idea is as follows: for any pair of -ltrations G and G a group G there is a club E such that for every E, G = G . So if we chose our set c in the denition of invariant to consist only of such good -s, namely if c E, then it does not matter according to which -ltration we work. But we cannot
modified:1996-03-19
choose a set c which is a subset of every club E resulting from some pair of -ltrations. What we can do is nd a sequence of c-s with the property that for every club E , stationarily many of them are subsets of E. Thus we will be able to dene an invariant that is independent of a particular choice of a -ltration. Here is the precise formulation of this:
revision:1994-06-16
1.5 Denition: A sequence c : S , where S is a stationary set, c and = sup c for every , is called a club guessing sequence if for every club E the set { S : c E} is a stationary subset of . The theorems asserting the existence of club guessing sequences will be quoted later. A club guessing sequence C = c : S gives rise to an ideal id(C) over the guessing ideal. 4
455
455
6.10.2003
1.6 Denition: Suppose that C = c : S is a club gussing sequence. We dene a proper ideal id(C) as follows: A id(C) A & E , E club, & E S, c E. So a set of -s is small if there is a club E which it fails to guess stationarily often, namely there is no A such that c E. 1.7 Lemma: If C is a club guessing sequence as above, then id(C) is a proper, complete ideal. Proof: That id(C) is proper means that it does not contains every subset of . Indeed, S id(C), as it guesses every club. That id(C) is downward closed is immediate from / the denition. Suppose, nally, that Ai , i < (), i() < are sets in the ideal. We show that their union A =
def i<i()
Ai is in the ideal. Pick a club Ei for every i < i() so that Ei is a club. Suppose that d A. Then there here
i<i()
Ai c Ei . The set E =
is some i < i() such that Ai . Therefore c Ei . But E Ei , so necessarily c E. Thus, A id(C)
modified:1996-03-19
1.7
We adopt the phrase for almost every in S, by which we mean for all S except for a set in id(C). 1.8 Lemma: Suppose that C = c : S is a club guessing sequence on S . Suppose that G and G are two -ltrations of a group G of cardinality . Then for almost every S, (1) holds for every g G. Proof: : The set of < for which G = Ga is a club. Let us denote it by E. If for some
revision:1994-06-16
, c E holds, then for every g G it is true that Inv G (g, c ) = InvG (g, c ). But as C is a club guessing sequence, by denition, for almost every , c E. We dene now the desired group invariant. 1.9 Denition: Suppose that C is a club guessing sequence and that G is a -ltration of a group G of cardinality . Let 5 1.8
455
6 (1) P (G, C) = {InvG (g, c ) : g G}
455
6.10.2003
(2) INV(G, C) = [ P (G, C) : S ]id(C) The second item should read the equivalence class of the sequence of P modulo the ideal id(C), where two sequences are equivalent modulo an ideal if the set of coordinate in which the sequences dier is in the ideal. 1.10 Lemma: The denition of INV(G, G) does not depend on the choice -ltration. Proof: Suppose that G, G are two -ltrations. By the regularity of , there exists a club E such that for every E, G = G . Therefore for every such that c E and every g G, InvG (g, c ) = InvG (g, c ). This means that for every such that c E, P (G, C) = P (G , C). But for almost all it is true that c E, therefore the sequqnces P (G, C) : S and P (G , C) : S are equivalent modulo id(C). 1.10
We remark at this point that the denition just made depends on the existence of a club guessing sequence! Strangely enough, we can prove the existence of club guessing sequences for regular uncountable cardinals for all such cardinals except 1 .
modified:1996-03-19
Let us now quote the relevant theorems which assert the existence of club guessing sequences: 1.11 Theorem: If and are cardinals, + < and is regular, then there is a club guessing sequence c : S such that the order type of each c is . Proof: In [Sh-e, new VI2]= [Sh-e, old III7]. We procced to show that INV is preserved, in a way, under pure embeddings.
revision:1994-06-16
1.12 Lemma: Suppose that H and G are groups of cardinality and that H and G are -ltrations. Suppose that C is a club guessing sequence on S . If h : H G is a pure embedding, then for almost every S P (H, C) P (G, C). Proof: Suppose for simplicity that H pr G, namely that the embedding is the identity function. The set E1 = { : H G = H } is a club. Dene for every natural number n 6
def
455
7 a function fn (y) on G as follows:
455
6.10.2003
some fn (y) =
x {x : x H & (x + y) nG}
if {x : x H & (x + y) nG} =
0 otherwise There is a club E2 such that G is closed under fn for all n for every E2 . E = E1 E2 is a club. 1.13 Claim: Suppose that h H and that E. Then h has an n-congruent in G (in the sense of G) i h has an n-congruent in H (in the sense of H). Proof: One direction is trivial. Suppose, then, that there is an n-congruent g G . Let h = fn (g). By the denition of fn , h + g nG ; also h g nG. Therefore h h nG. As H pr G, h h nH, and therefore h is an n-congruent of h in the sense of H. 1.13
The proof of the Lemma follows now readily: For almost every S it is true c E. Therefore for every such , every h H and every n, h has an n-congruent in H i h has an n-congruent in G . Therefore InvH (h, c ) InvG (h, c ).
modified:1996-03-19
1.12
2 Constructing groups with prescribed INV In this section we construct several groups with prescribed demands on their INV. These groups are used in the next section to show that in certain cardinals universal groups do not exist. The method in all constructions is attaching to a simply dened group points from a topological completion of the group. a. Constructions of p-groups
revision:1994-06-16
2.1 Theorem: If is a regular uncountable cardinal, C = c : S is a club guessing sequence and A c is a given set of order type , then there is a separable p-group G of cardinality and -ltration G such that A P (G, C) for every S. 2.2 Remark: This implies by Lemma 1.12 that for every separable p-group G of cardinality which purely extends G and a -ltration G , for almost every , A P (G , C) 7
455
8 Proof: For every n, let Bn =
n
455
6.10.2003
A where A is a copy of Zpn with generator a . Let
G0 =
n
Bn , and let G1 be the torsion completion of G0 . G1 may be identied with all
sequences (x1 , x2 , ) where xn Bn and such that there is a (nite) bound to {o(xn )}n . For details see [Fuchs II,1421]. The group we seek lies between G0 and G1 , and is a pure subgroup of G1 . Let us make a simple observation: (1) If x = (x1 , x2 , ) and y = (y1 , y2 , ) belong to G1 and x y pn G1 , then xi = yi for all i n. Proof: Let zi = xi yi . zi Bi . As Bi pn G1 = 0 for i n, we are done.
For every S let : n be the increasing enumeration of A . Denote by n n
the sequence , , . Let b0 G1 be (x , x , ) where x = pn1 an . So xn is of n 1 2 n 1 order p and height n 1. Consequently, b0 is of order p. Let us denote x def k = pn
modified:1996-03-19
pkn1 a 0
x
if n < k otherwise
and also let
0 def = pn
k 0. Let bn = ( , pn ). Let G be the subgroup of G1 generated by G0
together with {bn : S, n < }. Having dened G, let us specify a -ltration G. For every i < let Gi be {a : < i} {bn : S, < i, n < } . 2.3 Claim: InvG (b0 , c ) = A . Proof: We should show that the set of indices i with the property that in Gi+1 some congruent of b0 appears coincides with A . Suppose rst, then, that i = n for some n.
revision:1994-06-16
(x , , x , 0, 0, ) is clearly a pn -congruent of b , as b0 (x , , x ) = pn bn . Conversely, n 1 n 1 suppose that i < n and suppose to the contrary that there is some y = (y1 , y2 , ) Gi such that b0 y P n G. Then yi = xi for all i n by (1). But y Gi implies that yn Gi a contradiction to i < n . b. Constructions of torsion-free groups 8 2.3,2.1
455
455
6.10.2003
We start by constructing a torsion-free homogeneous group of a given type t = (, , , 0, ). We recall that a characteristic (g) of an element g G is the sequence (k1 , k2 , ) where kl is the p-height of g for the l-th prime. A height can be . A type t is an equivalence class of characteristics modulo the equivalence relation of having only a nite dierence in a nite number of coordinates. A homogeneous group is a group in which all elements have the same type. We call a type t a p-type if t = (, , , 0, ) where the only coordinate in which there is 0 is the number of p in the list of primes. 2.4 Theorem: For every uncountable and regular cardinal , a club guessing sequence C = c : S and given sets A c , each A of order type , there is a homogeneous group G of cardinality with p-type t and a -ltration G such that for every S, A P (G, C). 2.5 Remark: This means that for every pure extension G of G, for almost every S, A P (G , C). Proof: This proof resembles the proof of Theorem 2.1. Let G0 =
modified:1996-03-19
Qp (where Qp is the
group or rationals with denominators prime to p). We index the isomorphic copies of Q p by n and x a , an element a of characteristic (, , , 0, ) in the -th copy of Qp . Let G1 be the completion of G0 in the p-adic topology. Let (n) : n < be the
increasing enumeration of A , and let n = (0), , (n 1) . Let b,n = k
pkn ak . 2.4
The rest is as in the proof of Theorem 2.1. 3 The main results a. The Universality Spectrum of Torsion groups
revision:1994-06-16
There is universal torsion group in i there is a universal p-group in for every prime p. We therefore may focus on p-groups alone. There is a universal divisible p-group in , the group
Z(p ), therefore the rst interesting question to ask in torsion groups
is whether there is a universal reduced p-group. Here the answer is no: 9
455
10
455
6.10.2003
3.1 Theorem: If is an innite cardinal (not necessarily regular, not necessarily uncountable) then ther is no universal reduced p-group in . Proof: There are p-groups of cardinality of Ulm length for every ordinal < + . As u(A) u(B) whenever A B, and u(A) < + , for every group of cardinality , no p-group of cardinality can be universal. 3.1
We put a further restriction on the class of p-groups, by demanding that the Ulm length of a group be at most .1 We restrict ourselves then to the class of separable p-groups. On this class see [Fu] vol II, chapter XI. b. Universal separable p-groups We investigate the universality spectrum of the class or separable p-groups. 3.2 Theorem: If = 0 then there is a purely universal separable p-group in . Proof: Let B = Bn where Bn =
Zpn . The torsion completion of B, denoted by
G, is of cardinality |B|0 = 0 = and is puely universal in . To see this let A be
modified:1996-03-19
any separable p-group of cardinality , and let BA be its basic subgroup. BA is purely embeddable in B, and this gives rise to a pure embedding of A into G. 3.2
We see then, that for every n such that n 20 there is a purely universal separable p-group in n . As CH implies that in every 0 = n for all n, it follows by 3.2 that there n is a purely universal separable p-group in every n . It is not uncommon that CH decides questions in algebra. It is much less common, though, that a negation of CH or of GCH
revision:1994-06-16
does the same. The following theorem uses a negation of GCH as one of its hypotheses. 3.3 Theorem: is regular and there is some such that + < < 0 then there is no purely universal separable p-group in .
1
One can make ner distictions here by considering the class of all p-groups of Ulm
length which is bounded by an ordinal . But we do not do this here. 10
455
11
455
6.10.2003
Proof: By + < and Theorem 1.11, we may pick some club guessing sequence C = c : S where S is a stationary set of and otp c . Suppose G is a given separable p-group. We will show that G is not universal by presenting a separable p-group H of cardinality which is not embeddable in G. We choose a -ltration G of G and observe that |P (G, C)| for every . As 0 > , there is some A c , of order type , which dose not belong to P (G, C). By Theorem 2.1, there is a group H of cardinality such that for every embedding : H G, for almost every , A P (G, C). This can hold only emptily, that is, if there are no such embeddings, because A was chosen such that A P (G, C) / 3.3
3.4 Corollary: For n 2, there is a purely universal separable p-group in n if, and only if, 20 n . Proof: : If n 20 then 0 = n and by Theorem 3.2 there is a purely universal n separable p-group in n . Conversely, if n 2 and n < 20 , then by 3.3 there is no purely universal separable p-group in n
modified:1996-03-19
3.4
c. The Universality Spectrum of Torsion-Free Group We may restrict discussion in this Section to reduced torsion-free groups. We proceed to show rst that in regular which satisfy = 0 there is a universal reduced torsionfree group. The proof of the next theorem is an isolated point in the paper with respect to the technique, because it employs model theoretic notions (rst order theory, elementary embedding and saturated model). These are available in every standard textbook on model
revision:1994-06-16
theory, like [CK]. 3.5 Theorem: if = 0 20 , then there is a universal reduced torsion-free group in . Proof: Let T be a complete rst order theory of torsion free-groups. It is enough to nd a reduced group GT of cardinality such that GT |= T and for every H |= T , H is embedded 11
455
12
455
6.10.2003 GT is of cardinality (there are
T
in GT ; for if we have such a G for every T , the group
only 20 complete rst order theories), and is evidently universal. Let, then, GT be a saturated model of T of cardinality . Let D be its maximal division subgroup, and let GT = GT /D. GT is isomorphic to the direct summand of D, and is therefore torsion-free and reduced. Suppose that H |= T is reduced (and, clearly, torsion-free). There is an elementary embedding f : H GT . 3.6 Claim: Imf D = 0 Proof: Suppose 0 = a H and f (a) D. As f is elementary, a is divisible in H by every integer n. As H is torsion-free, the set of all divisors of a generates a divisible subgroup of H, contrary to H being reduced. We conclude, therefore, that f dened by f (a) = f (a) + D is an embedding of H into GT . 3.5 Next we show that below the continuum there is no purely-universal reduced torsionfree group. The reason for this is trivial: there are 20 types (over the empty set) in this
modified:1996-03-19
def
class. Therefore we do not need the club guessing machinery, and gain an extra case the case where = 1 in comparison to Corollary 3.4. 3.7 Theorem: If < 20 then there is no purely-universal reduced torsion-free group in cardinality . In fact, for every reduced torsion-free group G of cardinality there is a rank-1 group R which is not purely embeddable in G. Proof: As < 20 , there is a characteristic (k1 , k2 ), with all ki nite, which is not equal
revision:1994-06-16
to G (g) for every g G (The denitions of characteristic and type are from [Fu], II, 85). Let R be a rank-1 group such that R (1) = (k1 , k2 ). As pure embeddings preserve the characteristic, R is not purely embeddable in G. 3.7
We look now at a lasse of torsion-free groups which do not have many types above the empty set. This is the class of homogeneous groups (a group is homogeneous if all 12
455
13
455
6.10.2003
non zero elements in the group have the same type. See [Fu] II p.109). Here we are able again to prove that there is no purely universal group in the class in cardinality < 2 0 if > 1 . However, rather than using types over the empty wet, we are using invariants. 3.8 Theorem: If is a regular cardinal, + < < 0 for some , and t is a given p-type, then there is no purely universal torsion free group in . Even more, for every torsion free group of cardinality there is a homogeneous for the class of homogeneous groups whose type is t. Proof: Let G be any homogeneous group with type t, and x some -ltration G. Let C be a club guessing sequence, and for every S let A be such that A P (G, C). Such / an A exists, as |P (G, C)| < 20 , while there are 20 subsets of c . By Theorem 2.4, there is a homogeneous group H with type t such that A P (H, C) for every S. If there were a pure embedding : H G, then by Theorem 1.12, for almost every S, A would be in P (G, C). But by the choice of A this is impossible. 3.8
References
modified:1996-03-19
[CK] C. C Chang and J. J. Keisler Model Theory, North Holland 1973. [Fu] L. Fuchs, Innite Abelian Groups, vols. I, II, Academic press, 1970. [EM] P. C. Eklof and A. H. Mekler, Almost free Modules: Set theoretic methods North Holland Math. Library, 1990 [Sh-g] Saharon Shelah, Cardinal Arithmetic, to appear in OUP.
revision:1994-06-16
[KjSh 409] M. Kojman and S. Shelah, Existence of universal models, accepted to the Journal of Symbolic Logic [KjSh 447] M. Kojman and S. Shelah, The universality spectrum of stable unsuperstable theories, accepted to Annals of Pure and Applied Logic. [GrSh 174] R. Grossberg and S. Shelah, On universal locally nite groups, Israel J. of Math., 44, (1983), 289-302. 13
455
14
455
6.10.2003
Department of Mathematics Carnegie Mellon University Pittsburgh, PA 15 213 USA Institute for Mathematics The Hebrew University of Jerusalem, Jerusalem 91904
revision:1994-06-16
modified:1996-03-19
14
455
Anda mungkin juga menyukai
- Saharon Shelah - Zero One Laws For Graphs With Edge Probabilities Decaying With Distance. Part 1Dokumen42 halamanSaharon Shelah - Zero One Laws For Graphs With Edge Probabilities Decaying With Distance. Part 1JtyhmfBelum ada peringkat
- Saharon Shelah and Renling Jin - A Model in Which There Are Jech-Kunen Trees But There Are No Kupra TreesDokumen14 halamanSaharon Shelah and Renling Jin - A Model in Which There Are Jech-Kunen Trees But There Are No Kupra TreesJtyhmfBelum ada peringkat
- Saharon Shelah and Juris Steprans - Addendum To "Maximal Chains in Omega-Omega and Ultrapowers of The IntegersDokumen6 halamanSaharon Shelah and Juris Steprans - Addendum To "Maximal Chains in Omega-Omega and Ultrapowers of The IntegersJtyhmfBelum ada peringkat
- Saharon Shelah - The Generalized Continuum Hypothesis RevisitedDokumen44 halamanSaharon Shelah - The Generalized Continuum Hypothesis RevisitedJtyhmfBelum ada peringkat
- Saharon Shelah - Universal in ( Lambda) - Stable Abelian GroupDokumen12 halamanSaharon Shelah - Universal in ( Lambda) - Stable Abelian GroupJtyhmfBelum ada peringkat
- Saharon Shelah and Juris Steprans - Maximal Chains in Omega-Omega and Ultrapowers of The IntegersDokumen20 halamanSaharon Shelah and Juris Steprans - Maximal Chains in Omega-Omega and Ultrapowers of The IntegersJtyhmfBelum ada peringkat
- J. Baldwin, M. C. Laskowski and S. Shelah - Forcing IsomorphismDokumen18 halamanJ. Baldwin, M. C. Laskowski and S. Shelah - Forcing IsomorphismJtyhmfBelum ada peringkat
- P. C. Eklof and S. Shelah - Explicitly Non-Standard Uniserial ModulesDokumen16 halamanP. C. Eklof and S. Shelah - Explicitly Non-Standard Uniserial ModulesJtyhmfBelum ada peringkat
- Saharon Shelah - On The Very Weak 0-1 Law For Random Graphs With OrdersDokumen30 halamanSaharon Shelah - On The Very Weak 0-1 Law For Random Graphs With OrdersJtyhmfBelum ada peringkat
- Saharon Shelah - Sigma-Entangled Linear Orders and Narrowness of Products of Boolean AlgebrasDokumen95 halamanSaharon Shelah - Sigma-Entangled Linear Orders and Narrowness of Products of Boolean AlgebrasJtyhmfBelum ada peringkat
- Saharon Shelah - The Universality Spectrum: Consistency For More ClassesDokumen33 halamanSaharon Shelah - The Universality Spectrum: Consistency For More ClassesJtyhmfBelum ada peringkat
- Uri Abraham and Saharon Shelah - Martin's Axiom and Delta 2-1 Well-Ordering of The RealsDokumen16 halamanUri Abraham and Saharon Shelah - Martin's Axiom and Delta 2-1 Well-Ordering of The RealsJtyhmfBelum ada peringkat
- Menachem Kojman and Saharon Shelah - The Universality Spectrum of Stable Unsuperstable TheoriesDokumen25 halamanMenachem Kojman and Saharon Shelah - The Universality Spectrum of Stable Unsuperstable TheoriesJtyhmfBelum ada peringkat
- Garvin Melles and Saharon Shelah - Aut (M) Has A Large Dense Free Subgroup For Saturated MDokumen10 halamanGarvin Melles and Saharon Shelah - Aut (M) Has A Large Dense Free Subgroup For Saturated MJtyhmfBelum ada peringkat
- Saharon Shelah - Cardinalities of Topologies With Small BaseDokumen26 halamanSaharon Shelah - Cardinalities of Topologies With Small BaseJtyhmfBelum ada peringkat
- Tomek Bartoszynski and Saharon Shelah - Closed Measure Zero SetsDokumen20 halamanTomek Bartoszynski and Saharon Shelah - Closed Measure Zero SetsJtyhmfBelum ada peringkat
- Saharon Shelah - Cardinalities of Countably Based TopologiesDokumen6 halamanSaharon Shelah - Cardinalities of Countably Based TopologiesJtyhmfBelum ada peringkat
- Garvin Melles and Saharon Shelah - A Saturated Model of An Unsuperstable Theory of Cardinality Greater Than Its Theory Has The Small Index PropertyDokumen26 halamanGarvin Melles and Saharon Shelah - A Saturated Model of An Unsuperstable Theory of Cardinality Greater Than Its Theory Has The Small Index PropertyJtyhmfBelum ada peringkat
- P. C. Eklof, A. H. Mekler and S. Shelah - Uniformization and The Diversity of Whitehead GroupsDokumen19 halamanP. C. Eklof, A. H. Mekler and S. Shelah - Uniformization and The Diversity of Whitehead GroupsJtyhmfBelum ada peringkat
- Martin Goldstern and Saharon Shelah - Many Simple Cardinal InvariantsDokumen20 halamanMartin Goldstern and Saharon Shelah - Many Simple Cardinal InvariantsJtyhmfBelum ada peringkat
- Haim Judah and Saharon Shelah - Baire Property and Axiom of ChoiceDokumen15 halamanHaim Judah and Saharon Shelah - Baire Property and Axiom of ChoiceJtyhmfBelum ada peringkat
- Menachem Kojman and Saharon Shelah - Mu-Complete Souslin Trees On Mu +Dokumen8 halamanMenachem Kojman and Saharon Shelah - Mu-Complete Souslin Trees On Mu +JtyhmfBelum ada peringkat
- Saharon Shelah - Every Null-Additive Set Is Meager-AdditiveDokumen14 halamanSaharon Shelah - Every Null-Additive Set Is Meager-AdditiveJtyhmfBelum ada peringkat
- W. W. Comfort, Akio Kato and Saharon Shelah - Topological Partition Relations of The Form Omega - (Y) 1-2Dokumen15 halamanW. W. Comfort, Akio Kato and Saharon Shelah - Topological Partition Relations of The Form Omega - (Y) 1-2JtyhmfBelum ada peringkat
- Reinhard Diestel, Saharon Shelah and Juris Steprans - Characterizing Dominating GraphsDokumen9 halamanReinhard Diestel, Saharon Shelah and Juris Steprans - Characterizing Dominating GraphsJtyhmfBelum ada peringkat
- Martin Goldstern, Haim Judah and Saharon Shelah - Strong Measure Zero Sets Without Cohen RealsDokumen27 halamanMartin Goldstern, Haim Judah and Saharon Shelah - Strong Measure Zero Sets Without Cohen RealsJtyhmfBelum ada peringkat
- P. C. Eklof, A. H. Mekler and S. Shelah - Hereditarily Separable Groups and Monochromatic UniformizationDokumen23 halamanP. C. Eklof, A. H. Mekler and S. Shelah - Hereditarily Separable Groups and Monochromatic UniformizationJtyhmfBelum ada peringkat
- Maxim R. Burke and Saharon Shelah - Linear Liftings For Non-Complete Probability SpacesDokumen8 halamanMaxim R. Burke and Saharon Shelah - Linear Liftings For Non-Complete Probability SpacesJtyhmfBelum ada peringkat
- Tomek Bartoszynski and Saharon Shelah - Intersection of 2 Aleph Null Ultrafilters May Have Measure ZeroDokumen6 halamanTomek Bartoszynski and Saharon Shelah - Intersection of 2 Aleph Null Ultrafilters May Have Measure ZeroJtyhmfBelum ada peringkat
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDari EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifePenilaian: 4 dari 5 bintang4/5 (5783)
- The Yellow House: A Memoir (2019 National Book Award Winner)Dari EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Penilaian: 4 dari 5 bintang4/5 (98)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDari EverandNever Split the Difference: Negotiating As If Your Life Depended On ItPenilaian: 4.5 dari 5 bintang4.5/5 (838)
- Shoe Dog: A Memoir by the Creator of NikeDari EverandShoe Dog: A Memoir by the Creator of NikePenilaian: 4.5 dari 5 bintang4.5/5 (537)
- The Emperor of All Maladies: A Biography of CancerDari EverandThe Emperor of All Maladies: A Biography of CancerPenilaian: 4.5 dari 5 bintang4.5/5 (271)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDari EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RacePenilaian: 4 dari 5 bintang4/5 (890)
- The Little Book of Hygge: Danish Secrets to Happy LivingDari EverandThe Little Book of Hygge: Danish Secrets to Happy LivingPenilaian: 3.5 dari 5 bintang3.5/5 (399)
- Team of Rivals: The Political Genius of Abraham LincolnDari EverandTeam of Rivals: The Political Genius of Abraham LincolnPenilaian: 4.5 dari 5 bintang4.5/5 (234)
- Grit: The Power of Passion and PerseveranceDari EverandGrit: The Power of Passion and PerseverancePenilaian: 4 dari 5 bintang4/5 (587)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDari EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaPenilaian: 4.5 dari 5 bintang4.5/5 (265)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDari EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryPenilaian: 3.5 dari 5 bintang3.5/5 (231)
- On Fire: The (Burning) Case for a Green New DealDari EverandOn Fire: The (Burning) Case for a Green New DealPenilaian: 4 dari 5 bintang4/5 (72)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDari EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FuturePenilaian: 4.5 dari 5 bintang4.5/5 (474)
- Rise of ISIS: A Threat We Can't IgnoreDari EverandRise of ISIS: A Threat We Can't IgnorePenilaian: 3.5 dari 5 bintang3.5/5 (137)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDari EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersPenilaian: 4.5 dari 5 bintang4.5/5 (344)
- The Unwinding: An Inner History of the New AmericaDari EverandThe Unwinding: An Inner History of the New AmericaPenilaian: 4 dari 5 bintang4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDari EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyPenilaian: 3.5 dari 5 bintang3.5/5 (2219)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDari EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You ArePenilaian: 4 dari 5 bintang4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Dari EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Penilaian: 4.5 dari 5 bintang4.5/5 (119)
- Her Body and Other Parties: StoriesDari EverandHer Body and Other Parties: StoriesPenilaian: 4 dari 5 bintang4/5 (821)
- Composite and Decomposed FunctionsDokumen3 halamanComposite and Decomposed Functionsdaddy 'oBelum ada peringkat
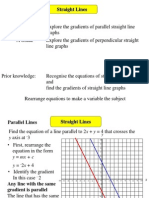
- Straight Lines 6-Parallel PerpendicularDokumen10 halamanStraight Lines 6-Parallel PerpendicularSelva RajBelum ada peringkat
- Fourth Form FinalExam Questions-2016Dokumen6 halamanFourth Form FinalExam Questions-2016Chet AckBelum ada peringkat
- EE5130 Problem Set 1 LTI Systems Convolution DTFTDokumen2 halamanEE5130 Problem Set 1 LTI Systems Convolution DTFTsoham1994Belum ada peringkat
- Introduction To Quantum Computing - Quantum Circuit ElementsDokumen13 halamanIntroduction To Quantum Computing - Quantum Circuit ElementsSaikiranKumarBelum ada peringkat
- Integration Formula: + C U Du VDX Udx DX V U Udx C CudxDokumen5 halamanIntegration Formula: + C U Du VDX Udx DX V U Udx C CudxRon AtaBelum ada peringkat
- Kristine Bobihis Cabalde, LPT, MSMEDokumen10 halamanKristine Bobihis Cabalde, LPT, MSMENorma MauiBelum ada peringkat
- On The Möbius Function in All Short Intervals Kaisa Matomäki, Joni TeräväinenDokumen18 halamanOn The Möbius Function in All Short Intervals Kaisa Matomäki, Joni TeräväinenSam TaylorBelum ada peringkat
- Sat Math Formula Practice - e Math AcademyDokumen6 halamanSat Math Formula Practice - e Math AcademytinlongBelum ada peringkat
- FormulaeDokumen8 halamanFormulaeDydtd FyfhBelum ada peringkat
- Lesson Exempla R: Quadratic Equations, Inequalities and Rational Algebraic EquationsDokumen6 halamanLesson Exempla R: Quadratic Equations, Inequalities and Rational Algebraic EquationsSWEETHEART BARRIONBelum ada peringkat
- Mathematics - Module 5Dokumen5 halamanMathematics - Module 5Angelo Luigi YasayBelum ada peringkat
- Lesson PlansDokumen12 halamanLesson Plansapi-282722668Belum ada peringkat
- (Mathematical Induction and Binomial Theorem) : Like Our Page For Entry Test Material & Admission UpdatesDokumen10 halaman(Mathematical Induction and Binomial Theorem) : Like Our Page For Entry Test Material & Admission UpdatesSAKBelum ada peringkat
- Differential Equations (MA 1150) Lecture 6: Fundamental Solutions and Constant Coefficient ODEsDokumen42 halamanDifferential Equations (MA 1150) Lecture 6: Fundamental Solutions and Constant Coefficient ODEsMansi NanavatiBelum ada peringkat
- More About Factorization of PolynomialsDokumen16 halamanMore About Factorization of PolynomialsFor BackupBelum ada peringkat
- FS Notes 1 PDFDokumen16 halamanFS Notes 1 PDFArkadev GhoshBelum ada peringkat
- Classifications of Ultrametric Spaces According To RoundnessDokumen12 halamanClassifications of Ultrametric Spaces According To RoundnessBob DylanBelum ada peringkat
- Algebra CR 2018 2 PDFDokumen4 halamanAlgebra CR 2018 2 PDFJhon AliagaBelum ada peringkat
- 3.1 Quadratic Functions and ModelsDokumen47 halaman3.1 Quadratic Functions and ModelsLeonardo TorresBelum ada peringkat
- Math 7 and 8 Performance TaskDokumen3 halamanMath 7 and 8 Performance Taskapi-401010000Belum ada peringkat
- Translating English into Algebraic ExpressionsDokumen2 halamanTranslating English into Algebraic ExpressionssalmanBelum ada peringkat
- Academic Council Proceedings May 2012Dokumen2 halamanAcademic Council Proceedings May 2012mridulkhandelwalBelum ada peringkat
- Teaching School Mathematics - AlgebraDokumen296 halamanTeaching School Mathematics - Algebrabelajar100% (3)
- Linear Algebra Resupply Date X. Dual SpaceDokumen5 halamanLinear Algebra Resupply Date X. Dual Space詹子軒Belum ada peringkat
- M01 MathematicsDokumen72 halamanM01 MathematicsDendi PerdanaBelum ada peringkat
- Addmath Form 4Dokumen11 halamanAddmath Form 4fariha ayuniBelum ada peringkat
- Ch.04 Force System ResultantsDokumen16 halamanCh.04 Force System ResultantsCK_85_3Belum ada peringkat
- Problem 1. Multilinear AlgebraDokumen4 halamanProblem 1. Multilinear Algebragau100% (5)