Poisson
Diunggah oleh
Shobha SinghDeskripsi Asli:
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Poisson
Diunggah oleh
Shobha SinghHak Cipta:
Format Tersedia
POISSON DISTRIBUTION
Examples
1. Number of telephone calls in a week.
2. Number of people arriving at a checkout in a
day.
3. Number of industrial accidents per month in a
manufacturing plant.
Generally
X = number of events, distributed independently
in time, occurring in a xed time interval.
X is a Poisson variable with pdf:
P(X = x) = e
x
x!
, x = 0, 1, . . . ,
where is the average.
1
Example 1:
If the number of arrivals is 10 per hour on average,
determine the probability that, in any hour there
will be
(i) 0 arrivals;
(ii) 6 arrivals;
(iii) more than 6 arrivals.
2
Example 2:
The average rate of telephone calls in a busy recep-
tion is 4 per minute. If it can be assumed that the
number of telephone calls per minute interval is
Poisson distributed, calculate the probability that
(i) at least 2 telephone calls will be received in any
minute.
(ii) any minute will be free of telephone calls.
(iii) no more than one telephone call will be received
in any one minute interval.
3
Derivations of Some Properties of
Poisson
1. Clearly
e
x
x!
> 0 since > 0
Also
x=0
e
x
x!
= 1
since
e
= 1 + +
2
2!
+
3
3!
+
i.e.
x=0
x
x!
= e
4
2. E(X) =
E(X) =
x=0
xe
x
x!
= e
x=1
x
x
x!
= e
x=1
x
(x 1)!
= e
x=1
x1
(x 1)!
_
_
= e
_1 +
1!
+
2
2!
+ . . .
_
_
= e
=
5
APPLICATIONS OF THE POISSON
The Poisson distribution arises in two ways:
1. As an approximation to the binomial when p
is small and n is large
Example: In auditing when examining accounts for
errors; n, the sample size, is usually large. p, the er-
ror rate, is usually small.
2. Events distributed independently of one an-
other in time:
X = the number of events occurring in a xed time
interval has a Poisson distribution.
Example: X = the number of telephone calls in
an hour.
PDF : p(x) = e
x
x!
, x = 0, 1, 2, ; > 0
6
Poisson Approximation to the Binomial
When the sample size n is large and the occurrence p is
small, the pdfs of the Binomial and Poisson are similar.
Example: An audit consists of inspecting 100 line
items selected from a large accounting population. The
accounts are rejected if more than three errors are found
in the sample. Past experience indicates that, on aver-
age, 2% of the accounts have been misstated. Calculate
the probability of rejecting the whole set.
Binomial Poisson
Approximation
x
_
100
x
_
.02
x
.98
100x
e
2
2
x
/x!
0 0.13262 0.13534
1 0.27065 0.27067
2 0.27341 0.27067
3 0.18228 0.18045
Total 0.85890 0.85713
Rule of Thumb: Use Poisson Approximation to
Binomial when n 30 and p .05.
7
Poisson as an approximation to the binomial
when n is large p is small
Recall:
mean of binomial = np
mean of Poisson =
PDF of Binomial
P(x) =
_
_
n
x
_
_
p
x
(1 p)
nx
; p =
n
=
_
_
n
x
_
_
_
n
_
x
_
1
n
_
nx
=
n!
x!(n x)!
x
n
x
(1
n
)
n
_
1
n
_
x
x
x!
e
Now
(1
n
)
n
e
as n
(1
n
)
x
1 as n
n!
(n x)!n
x
=
n(n 1) . . . (n (x 1))
n
x
= 1(1
1
n
)(1
2
n
) . . . (1
x 1
n
) 1
8
Example 1:
An auditor with a rm, running a chain of shops, believes
that the number of errors in its invoices follows a Poisson
distribution. To test the hypothesis, 100 shops were ob-
served and the invoices were inpsected. The distribution
of the number of errors found were as follows:
Errors 0 1 2 3 4 5
No. Shops 16 34 27 12 7 4
Example 2:
An auditor selects a simple random sample of line items
to decide whether or not to audit the full set. If more
than 10% of the sample are misstated, the entire set will
be audited. In each of the following circumstances, esti-
mate the probability of this happening when the popu-
lation contains 5% misstated accounts:
1. A sample of 10 is selected from a set of 40;
2. A sample of 10 is selected from a set of 5,000;
3. A sample of 50 is selected from a set of 5,000.
9
Anda mungkin juga menyukai
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDari EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifePenilaian: 4 dari 5 bintang4/5 (5795)
- January 2005 6-1 6-101: Local Governments, and Non-Profit OrganizationsDokumen31 halamanJanuary 2005 6-1 6-101: Local Governments, and Non-Profit OrganizationsDoxCak3Belum ada peringkat
- Grit: The Power of Passion and PerseveranceDari EverandGrit: The Power of Passion and PerseverancePenilaian: 4 dari 5 bintang4/5 (588)
- Haitham AL-Qawasmi: PersonalDokumen3 halamanHaitham AL-Qawasmi: PersonalSalam NaddafBelum ada peringkat
- The Yellow House: A Memoir (2019 National Book Award Winner)Dari EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Penilaian: 4 dari 5 bintang4/5 (98)
- Office Safety Checklist: Housekeeping Yes No N/ADokumen2 halamanOffice Safety Checklist: Housekeeping Yes No N/Aahmar javed100% (1)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDari EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RacePenilaian: 4 dari 5 bintang4/5 (895)
- DocumentDokumen5 halamanDocumentSamira PatrickBelum ada peringkat
- Shoe Dog: A Memoir by the Creator of NikeDari EverandShoe Dog: A Memoir by the Creator of NikePenilaian: 4.5 dari 5 bintang4.5/5 (537)
- Pre IPO ChecklistDokumen13 halamanPre IPO ChecklistNaresh PatroBelum ada peringkat
- The Emperor of All Maladies: A Biography of CancerDari EverandThe Emperor of All Maladies: A Biography of CancerPenilaian: 4.5 dari 5 bintang4.5/5 (271)
- Performance of An Accountancy School in Certified Public Accountant Licensure Examinations in The PhilippinesDokumen8 halamanPerformance of An Accountancy School in Certified Public Accountant Licensure Examinations in The PhilippinesB0bby M0ntuyaBelum ada peringkat
- The Little Book of Hygge: Danish Secrets to Happy LivingDari EverandThe Little Book of Hygge: Danish Secrets to Happy LivingPenilaian: 3.5 dari 5 bintang3.5/5 (400)
- H. QuestionnaireDokumen5 halamanH. QuestionnaireJASMIN TUBOBelum ada peringkat
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDari EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FuturePenilaian: 4.5 dari 5 bintang4.5/5 (474)
- Quarterly Status Report On Implementation of SAI June 2018Dokumen4 halamanQuarterly Status Report On Implementation of SAI June 2018RodolfoBelum ada peringkat
- On Fire: The (Burning) Case for a Green New DealDari EverandOn Fire: The (Burning) Case for a Green New DealPenilaian: 4 dari 5 bintang4/5 (74)
- EM01Dokumen20 halamanEM01Anonymous B7pghh100% (1)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDari EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersPenilaian: 4.5 dari 5 bintang4.5/5 (345)
- IFRS 1 - For PresDokumen27 halamanIFRS 1 - For Presnati67% (3)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDari EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryPenilaian: 3.5 dari 5 bintang3.5/5 (231)
- Cost Accounting-Notes For PrelimDokumen18 halamanCost Accounting-Notes For PrelimAngelie BancaleBelum ada peringkat
- Never Split the Difference: Negotiating As If Your Life Depended On ItDari EverandNever Split the Difference: Negotiating As If Your Life Depended On ItPenilaian: 4.5 dari 5 bintang4.5/5 (838)
- OpenDokumen3 halamanOpenntv2000Belum ada peringkat
- Chap 020Dokumen44 halamanChap 020JanitscharenBelum ada peringkat
- Team of Rivals: The Political Genius of Abraham LincolnDari EverandTeam of Rivals: The Political Genius of Abraham LincolnPenilaian: 4.5 dari 5 bintang4.5/5 (234)
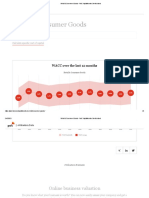
- Retail & Consumer Goods - PWC Kapitalkosten DeutschlandDokumen6 halamanRetail & Consumer Goods - PWC Kapitalkosten DeutschlandJavi FernandezBelum ada peringkat
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDari EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaPenilaian: 4.5 dari 5 bintang4.5/5 (266)
- Banking RFP Template Not For ProfitDokumen2 halamanBanking RFP Template Not For ProfitJill MarinoBelum ada peringkat
- Auditing Theory - Day 01Dokumen3 halamanAuditing Theory - Day 01Rafael Renz DayaoBelum ada peringkat
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDari EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyPenilaian: 3.5 dari 5 bintang3.5/5 (2259)
- Estimation ManualDokumen32 halamanEstimation Manualmayur_lanjewarBelum ada peringkat
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDari EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You ArePenilaian: 4 dari 5 bintang4/5 (1091)
- Corrective and Preventive Action Request Form: Pt. Akura Bina CitraDokumen1 halamanCorrective and Preventive Action Request Form: Pt. Akura Bina CitraAndreasSembiringBelum ada peringkat
- Pertemuan 12-Audit SamplingDokumen10 halamanPertemuan 12-Audit SamplingWawa LalaBelum ada peringkat
- Math 12 ABM Organization - MGT Q2 Week 6Dokumen15 halamanMath 12 ABM Organization - MGT Q2 Week 6Sammy MateoBelum ada peringkat
- Root Cause Corrective Action: SolveDokumen153 halamanRoot Cause Corrective Action: Solvehagh_mostafa2787Belum ada peringkat
- Rise of ISIS: A Threat We Can't IgnoreDari EverandRise of ISIS: A Threat We Can't IgnorePenilaian: 3.5 dari 5 bintang3.5/5 (137)
- Enron CorpDokumen8 halamanEnron CorpShanthana LoshiniBelum ada peringkat
- The Unwinding: An Inner History of the New AmericaDari EverandThe Unwinding: An Inner History of the New AmericaPenilaian: 4 dari 5 bintang4/5 (45)
- 03 Bidding Procedure For Goods and InfraDokumen96 halaman03 Bidding Procedure For Goods and InfraJuliefe Magbata ApostolBelum ada peringkat
- CVDokumen2 halamanCVruslan3089Belum ada peringkat
- Shezan AR 2016Dokumen64 halamanShezan AR 2016Nisar Akbar KhanBelum ada peringkat
- Practice Standards and Ethical ConsiderationsDokumen25 halamanPractice Standards and Ethical ConsiderationsJohn AlbateraBelum ada peringkat
- QUALITY MANAGEMENT MCQsDokumen6 halamanQUALITY MANAGEMENT MCQsWedad aliBelum ada peringkat
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Dari EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Penilaian: 4.5 dari 5 bintang4.5/5 (121)
- Food Distribution Monitoring System GUIDELINESDokumen3 halamanFood Distribution Monitoring System GUIDELINESطلال مداحBelum ada peringkat
- Apha 1020QCDokumen10 halamanApha 1020QCErick Leonardo Valle MendozaBelum ada peringkat
- Control and Performance EvaluationDokumen83 halamanControl and Performance EvaluationRafaelDelaCruzBelum ada peringkat
- Her Body and Other Parties: StoriesDari EverandHer Body and Other Parties: StoriesPenilaian: 4 dari 5 bintang4/5 (821)