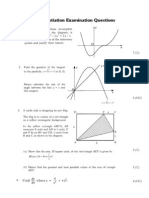
Unit1 Summary
Diunggah oleh
knoxmathsHak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Unit1 Summary
Diunggah oleh
knoxmathsHak Cipta:
Format Tersedia
hsn.uk.
net
Straight Lines
Distance Formula 2 2 Distance = ( x2 x1 ) + ( y2 y1 ) betw een ( x1, y1 ) and ( x2 , y2 ) Midpoint Formula
x +x y + y Midpoint = 1 2 , 1 2 2 2
m = tan
Notation
Functions and Graphs
Composite Functions
Example
f (x ) = x2 +1 f ( g( x )) = f (3x 4 ) = (3x 4 ) + 1
2
bel ongs to naturalnum bers { 1, 2, 3, ...}
Higher Mathematics HSN21500
g( f ( x ))
integers { ... , 1, 0,1, 2, ...} rational integer f ractions
w hol num bers { 0,1, 2, 3, ...} e
Rules
Differentiation
g ( x ) = 3x 4
= g ( x 2 + 1)
= 3 ( x 2 + 1) 4
real al points on the num ber l l ine
Domains
Set ofnum bers a f unction can operate on R estrictions Cannot divide by zero Cannot take even roots (eg square root) of negative num bers
If f ( x ) = ax n then f ( x ) = anx n1 pow er m ul ies to the f tipl ront, pow er l ers by one ow Preparing to differentiate Mul y out brackets tipl
Radians
Gradients
y y m= 2 1 x2 x1
radians = 180
Graphs of Inverses
Degrees
180 180
R efect in the l y = x , eg l ine l ogarithm ic and exponential y y = ax Radians y=x (1, a )
y=l ax og
Rates of Change
x = x2 1 Put al x term s on the top l eg 32 = 3x 2 and 1 = x 2 l ine, x x
Change roots into pow ers, eg
f ( a ) is the rate of change of f ( x ) at x = a .
Equations of Tangents
positive negative zero undefined gradient gradient gradient gradient
Paralell l ines have equalgradients
Exact Values
2 45
Graph Transformations
Transl ation: f ( x ) + a, f ( x + a ) R ef ection: f ( x ), f ( x ) l Scal ing: kf ( x ), f ( kx )
2 30 3
60
1 O 1
( a ,1)
x
A tangent is a straight l to use y b = m ( x a ) w e need a ine point and a gradient One coordinate of the point w il al ays be given the other can l w be w orked out using the given equation The gradient is a rate of change dif erentiate and substitute in f
x-coord. ( dx is the equation of the gradient)
dy dx
dy
Perpendicular Lines
45
m1 m2 = 1 f tw o l at right or ines angl w ith gradients m1 and m2 es,
Collinearity
The gradient betw een tw o of the points is equalto the gradient betw een tw o other points They share a com m on point
Equation of a Straight Line
y b = m(x a) ( a, b ) is a point on the line m is the l s gradient ine
Unit 1
Sequences
Al inear recurrence rel ation can be w ritten in the f orm un +1 = aun + b or un = aun1 + b (both m ean exactl the sam e thing) y If 1 < a < 1 then a l inear recurrence rel ation w il l cul have a l it l, w hich can be cal ated using l = b im 1 a
Increasing and Decreasing Functions
> 0 increasing,
Stationary Points
dy dx
< 0 decreasing
Occur w hen f ( x ) = 0 Four possibil ities f nature (use a nature tabl or e):
Intersection of two lines
Sol sim ul ve taneous equations (the equations of the tw o l ines) El ination, equating or substitution im
not collinear not collinear C D A C B
collinear
Perpendicular Bisectors
D A C B
maximum turning point
minimum turning point
rising point of inflection
falling point of inflection
Medians
B
Altitudes
B
Curve sketching
Graphs of Derived Functions
y Al stationary points l decreasing (ve gradient) increasing becom e roots increasing (+ve gradient) (+ve gradient) When the graph is x increasing, the graph of the derivative is y above the x-axis above above x-axis x-axis When the graph is x below x-axis decreasing, the graph of the derivative is bel the x-axis ow
BM is a m edian M is the m idpoint of AC Median from B Point: B or M G radient: mBM
CD is a perpendicul ar bisector of AB D BD is an al titude CD passes through the BD is perp. to AC m idpoint of AB Perpendicul bisector of A B ar Al titude from B Point: B Point: m idpoint of AB G radient: mCD G radient: mBD mCD mAB = 1 mBD mAC = 1
A
Work out x-axis intercepts (roots) sol y = 0 ve Work out y-axis intercept f y f x = 0 ind or Determ ine stationary points and their nature (use a nature tabl e)
Closed Intervals (Restricted Domains)
Max/m in val can occur at stationary points, or end points of ues the cl osed interval
Optimisation
Probl s usualy invol f em l ve inding m ax/m in areas and vol es um ( x ) = 0 ) and determ ine its nature Cal ate a stationary point ( f cul (use a nature tabl e)
Anda mungkin juga menyukai
- Unit 1 Notes PDFDokumen18 halamanUnit 1 Notes PDFCharles GribbenBelum ada peringkat
- SAT II Math Level 2 Subject Test Notes: FunctionsDokumen3 halamanSAT II Math Level 2 Subject Test Notes: Functionstomcantyyy100% (2)
- C1 Revision NotesDokumen5 halamanC1 Revision Notesxxtrim100% (1)
- Formulas SheetDokumen5 halamanFormulas SheetabdulrehmanBelum ada peringkat
- Important Points and Formulae: e Markedpric Discount Loss ProfitDokumen5 halamanImportant Points and Formulae: e Markedpric Discount Loss ProfitNyasha GweruBelum ada peringkat
- Math SL HandoutDokumen15 halamanMath SL Handoutmikalala1105Belum ada peringkat
- Cantey - Calculus Memory BookDokumen18 halamanCantey - Calculus Memory BookscottswallowsBelum ada peringkat
- Add Maths Formulae ListDokumen8 halamanAdd Maths Formulae ListWong Hui SeanBelum ada peringkat
- A-level Maths Revision: Cheeky Revision ShortcutsDari EverandA-level Maths Revision: Cheeky Revision ShortcutsPenilaian: 3.5 dari 5 bintang3.5/5 (8)
- SPM Add Maths Formula List Form4 PDFDokumen16 halamanSPM Add Maths Formula List Form4 PDFNicholas Rogers80% (5)
- Maths Concepts and Formulae: y FX F y XDokumen16 halamanMaths Concepts and Formulae: y FX F y XAt TanwiBelum ada peringkat
- Algebra FormulasDokumen12 halamanAlgebra FormulasLuis Fernando De AlvarengaBelum ada peringkat
- MathematicsDokumen7 halamanMathematicsJay LiBelum ada peringkat
- Vector Calculus ReviewDokumen45 halamanVector Calculus ReviewJoshua CookBelum ada peringkat
- Sunway College Johor Bahru Cambridge Gce A-Levels Programme 9709 - Mathematics Paper 1 SummaryDokumen7 halamanSunway College Johor Bahru Cambridge Gce A-Levels Programme 9709 - Mathematics Paper 1 SummaryLehleh HiiBelum ada peringkat
- Writing and Graphing Linear Equations 1 1Dokumen62 halamanWriting and Graphing Linear Equations 1 1api-32711519150% (2)
- Important Points and Formulae: Mathematics Grade 9 BmiDokumen6 halamanImportant Points and Formulae: Mathematics Grade 9 BmiZulfiqar Ali MirBelum ada peringkat
- Important Points and Formulae: e Markedpric Discount Loss ProfitDokumen4 halamanImportant Points and Formulae: e Markedpric Discount Loss ProfitTaha YousafBelum ada peringkat
- Calculus II Cheat SheetDokumen4 halamanCalculus II Cheat SheetajznelsonBelum ada peringkat
- Algebra FormulasDokumen12 halamanAlgebra FormulasAmir MustakimBelum ada peringkat
- Math - 7th Grade Teaching NotesDokumen16 halamanMath - 7th Grade Teaching NotesPara ParadiseBelum ada peringkat
- Ad Maths Formula ListDokumen16 halamanAd Maths Formula ListZareena CarrimBelum ada peringkat
- SAT Subject Math Level 2 FactsDokumen11 halamanSAT Subject Math Level 2 FactsSalvadorBelum ada peringkat
- Linear Graphs and Equations: Y1 M (x-x1) When The Gradient and The Co-Ordinates (x1, Y1) of A Single Point That The LineDokumen6 halamanLinear Graphs and Equations: Y1 M (x-x1) When The Gradient and The Co-Ordinates (x1, Y1) of A Single Point That The LineSchoolSlackerBelum ada peringkat
- Mathematics Revision of Formulae and Results: Surds Co-Ordinate GeometryDokumen5 halamanMathematics Revision of Formulae and Results: Surds Co-Ordinate GeometryabhiBelum ada peringkat
- Unit 2 SummaryDokumen1 halamanUnit 2 SummaryknoxmathsBelum ada peringkat
- SPM Add Maths Formula List Form4Dokumen16 halamanSPM Add Maths Formula List Form4Alvin HonBelum ada peringkat
- Geometry: Steven SkienaDokumen22 halamanGeometry: Steven SkienapropatrioBelum ada peringkat
- C1 Maths Revision Algebra and Functions (Chapter 1)Dokumen12 halamanC1 Maths Revision Algebra and Functions (Chapter 1)Laurence GardnerBelum ada peringkat
- 0.2 Lines in The Plane: The Real Number LineDokumen14 halaman0.2 Lines in The Plane: The Real Number Linebenalyn ignacioBelum ada peringkat
- Graphs, Linear Equations, and FunctionsDokumen46 halamanGraphs, Linear Equations, and FunctionsAmit BhararaBelum ada peringkat
- HSCMaths Ext 231341Dokumen30 halamanHSCMaths Ext 231341Robert HigginsBelum ada peringkat
- AnalyticDokumen25 halamanAnalyticshotsfiredsxiiiBelum ada peringkat
- Formula Sheet MathDokumen5 halamanFormula Sheet MathMata Pronoob100% (1)
- 1385106121Dokumen70 halaman1385106121Abhishek AgrawalBelum ada peringkat
- Calculus Book IDokumen19 halamanCalculus Book ITeresa Villena GonzálezBelum ada peringkat
- Straight Lines HSNDokumen18 halamanStraight Lines HSNapi-298592212Belum ada peringkat
- C2 RevisionDokumen2 halamanC2 RevisionEL HassaryBelum ada peringkat
- Additional Mathematics - List of Formulae (Form 4)Dokumen19 halamanAdditional Mathematics - List of Formulae (Form 4)Syazleen Nabilah AkmalBelum ada peringkat
- Transformation of Axes (Geometry) Mathematics Question BankDari EverandTransformation of Axes (Geometry) Mathematics Question BankPenilaian: 3 dari 5 bintang3/5 (1)
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsDari EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsBelum ada peringkat
- Applications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankDari EverandApplications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankBelum ada peringkat
- Practice Makes Perfect in Geometry: Angles, Triangles and other PolygonsDari EverandPractice Makes Perfect in Geometry: Angles, Triangles and other PolygonsPenilaian: 5 dari 5 bintang5/5 (1)
- Harmonic Maps and Minimal Immersions with Symmetries (AM-130), Volume 130: Methods of Ordinary Differential Equations Applied to Elliptic Variational Problems. (AM-130)Dari EverandHarmonic Maps and Minimal Immersions with Symmetries (AM-130), Volume 130: Methods of Ordinary Differential Equations Applied to Elliptic Variational Problems. (AM-130)Belum ada peringkat
- Nonlinear Functional Analysis and Applications: Proceedings of an Advanced Seminar Conducted by the Mathematics Research Center, the University of Wisconsin, Madison, October 12-14, 1970Dari EverandNonlinear Functional Analysis and Applications: Proceedings of an Advanced Seminar Conducted by the Mathematics Research Center, the University of Wisconsin, Madison, October 12-14, 1970Louis B. RallBelum ada peringkat
- Application of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsDari EverandApplication of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsPenilaian: 5 dari 5 bintang5/5 (1)
- Practice Makes Perfect in Geometry: Angles, Triangles and other Polygons with AnswersDari EverandPractice Makes Perfect in Geometry: Angles, Triangles and other Polygons with AnswersBelum ada peringkat
- Practice Makes Perfect in Geometry: Three-Dimensional FiguresDari EverandPractice Makes Perfect in Geometry: Three-Dimensional FiguresBelum ada peringkat
- A5 Summer School 2012 3 FlyerDokumen2 halamanA5 Summer School 2012 3 FlyerknoxmathsBelum ada peringkat
- Zot VacDokumen1 halamanZot VacknoxmathsBelum ada peringkat
- Technicians AdvertDokumen1 halamanTechnicians AdvertknoxmathsBelum ada peringkat
- 16+ EventDokumen1 halaman16+ EventknoxmathsBelum ada peringkat
- Recruitment Poster EdinurghDokumen1 halamanRecruitment Poster EdinurghknoxmathsBelum ada peringkat
- Unit 2 Integration Examination Questions CALDokumen4 halamanUnit 2 Integration Examination Questions CALknoxmathsBelum ada peringkat
- Muirfield VacDokumen1 halamanMuirfield VacknoxmathsBelum ada peringkat
- Unit 2 Recurrence Relation Examination Questions CALDokumen4 halamanUnit 2 Recurrence Relation Examination Questions CALknoxmathsBelum ada peringkat
- Unit 1 Straight Line Exam Questions CALDokumen3 halamanUnit 1 Straight Line Exam Questions CALknoxmathsBelum ada peringkat
- U2 Trigonometric Formulae and EquationsDokumen4 halamanU2 Trigonometric Formulae and EquationsknoxmathsBelum ada peringkat
- U2 Equation of CircleDokumen7 halamanU2 Equation of CircleknoxmathsBelum ada peringkat
- U2 Factors and Quadratic TheoryDokumen3 halamanU2 Factors and Quadratic TheoryknoxmathsBelum ada peringkat
- Credit Past Paper Questions - SolutionsDokumen28 halamanCredit Past Paper Questions - SolutionsknoxmathsBelum ada peringkat
- Advanced Higher Maths: Formulae: Essential Trigonometric IdentitiesDokumen5 halamanAdvanced Higher Maths: Formulae: Essential Trigonometric IdentitiesknoxmathsBelum ada peringkat
- Unit 1 Differentiation Examination Questions CALDokumen6 halamanUnit 1 Differentiation Examination Questions CALknoxmathsBelum ada peringkat
- U1 Graphs and FunctionsDokumen4 halamanU1 Graphs and FunctionsknoxmathsBelum ada peringkat
- Higher Unit 3 SummaryDokumen1 halamanHigher Unit 3 SummaryknoxmathsBelum ada peringkat
- Unit 2 SummaryDokumen1 halamanUnit 2 SummaryknoxmathsBelum ada peringkat
- Unit RevisionDokumen7 halamanUnit RevisionknoxmathsBelum ada peringkat
- Differentiation FormulaeDokumen3 halamanDifferentiation FormulaeknoxmathsBelum ada peringkat
- Standard Integrals Formulae 1Dokumen1 halamanStandard Integrals Formulae 1knoxmathsBelum ada peringkat
- S3 April Credit Assessment: 1. Calculation 2. Scientific Notation 3. SimilarityDokumen1 halamanS3 April Credit Assessment: 1. Calculation 2. Scientific Notation 3. SimilarityknoxmathsBelum ada peringkat
- Revision Questions by TopicDokumen82 halamanRevision Questions by TopicknoxmathsBelum ada peringkat
- S3 December Credit AssessmentDokumen1 halamanS3 December Credit AssessmentknoxmathsBelum ada peringkat
- S2 Course OutlineDokumen1 halamanS2 Course OutlineknoxmathsBelum ada peringkat
- S1 Course OutlineDokumen1 halamanS1 Course OutlineknoxmathsBelum ada peringkat
- Python in Hidrology BookDokumen153 halamanPython in Hidrology BookJuan david Gonzalez vasquez100% (1)
- 25 Middlegame Concepts Every Chess Player Must KnowDokumen2 halaman25 Middlegame Concepts Every Chess Player Must KnowKasparicoBelum ada peringkat
- European Asphalt Standards DatasheetDokumen1 halamanEuropean Asphalt Standards DatasheetmandraktreceBelum ada peringkat
- Jul - Dec 09Dokumen8 halamanJul - Dec 09dmaizulBelum ada peringkat
- 3D Printing & Embedded ElectronicsDokumen7 halaman3D Printing & Embedded ElectronicsSantiago PatitucciBelum ada peringkat
- Angle Modulation: Hệ thống viễn thông (Communication Systems)Dokumen41 halamanAngle Modulation: Hệ thống viễn thông (Communication Systems)Thành VỹBelum ada peringkat
- PDFDokumen40 halamanPDFAndi NursinarBelum ada peringkat
- Grade 8 Science - Second GradingDokumen5 halamanGrade 8 Science - Second GradingMykelCañete0% (1)
- Breastfeeding W Success ManualDokumen40 halamanBreastfeeding W Success ManualNova GaveBelum ada peringkat
- MFE Module 1 .Dokumen15 halamanMFE Module 1 .Adarsh KBelum ada peringkat
- Financial Market - Bsa 2A Dr. Ben E. Bunyi: Imus Institute of Science and TechnologyDokumen3 halamanFinancial Market - Bsa 2A Dr. Ben E. Bunyi: Imus Institute of Science and TechnologyAsh imoBelum ada peringkat
- Note!: Rear Shock Absorber For YAMAHA N-MAXDokumen4 halamanNote!: Rear Shock Absorber For YAMAHA N-MAXAdityaArnas0% (1)
- Ch-10 Human Eye Notes FinalDokumen27 halamanCh-10 Human Eye Notes Finalkilemas494Belum ada peringkat
- PDFDokumen27 halamanPDFER Saurabh KatariyaBelum ada peringkat
- SW OSDokumen11 halamanSW OSErnest OfosuBelum ada peringkat
- Grade 3 - Unit 1 Increase and Decrease PatternDokumen7 halamanGrade 3 - Unit 1 Increase and Decrease PatternKyo ToeyBelum ada peringkat
- Biotech NewsDokumen116 halamanBiotech NewsRahul KapoorBelum ada peringkat
- The Rise of Australian NovelDokumen412 halamanThe Rise of Australian NovelSampath Kumar GummadiBelum ada peringkat
- Institutional Group Agencies For EducationDokumen22 halamanInstitutional Group Agencies For EducationGlory Aroma100% (1)
- Coaxial Cable Attenuation ChartDokumen6 halamanCoaxial Cable Attenuation ChartNam PhamBelum ada peringkat
- Cobol v1Dokumen334 halamanCobol v1Nagaraju BBelum ada peringkat
- 8 A - 1615864446 - 1605148379 - 1579835163 - Topic - 8.A.EffectiveSchoolsDokumen9 halaman8 A - 1615864446 - 1605148379 - 1579835163 - Topic - 8.A.EffectiveSchoolsYasodhara ArawwawelaBelum ada peringkat
- Contoh Exposition TextDokumen1 halamanContoh Exposition TextKristin SeranBelum ada peringkat
- The Mooring Pattern Study For Q-Flex Type LNG Carriers Scheduled For Berthing at Ege Gaz Aliaga LNG TerminalDokumen6 halamanThe Mooring Pattern Study For Q-Flex Type LNG Carriers Scheduled For Berthing at Ege Gaz Aliaga LNG TerminalMahad Abdi100% (1)
- Sundar Pichai PDFDokumen6 halamanSundar Pichai PDFHimanshi Patle100% (1)
- Quality Control of Rigid Pavements 1Dokumen58 halamanQuality Control of Rigid Pavements 1pranjpatil100% (1)
- Word CountDokumen3 halamanWord CountLeo LonardelliBelum ada peringkat
- Chapter 10 Tute Solutions PDFDokumen7 halamanChapter 10 Tute Solutions PDFAi Tien TranBelum ada peringkat
- Safety Data Sheet SDS For CB-G PG Precision Grout and CB-G MG Multipurpose Grout Documentation ASSET DOC APPROVAL 0536Dokumen4 halamanSafety Data Sheet SDS For CB-G PG Precision Grout and CB-G MG Multipurpose Grout Documentation ASSET DOC APPROVAL 0536BanyuBelum ada peringkat
- Multinational MarketingDokumen11 halamanMultinational MarketingraghavelluruBelum ada peringkat