05246004
Diunggah oleh
bobmilkmanDeskripsi Asli:
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
05246004
Diunggah oleh
bobmilkmanHak Cipta:
Format Tersedia
Proceedings of the 2009 IEEE
International Conference on Mechatronics and Automation
August 9 - 12, Changchun, China
Dynamics Modeling of an Unmanned Bicycle with
Parallel Mechanism Adjusting Stability
Yanbin Liu
School ofMechatronical Engineering
University ofScience and Technology
Henan
Luoyang, Henan Province, China
Ihybxy@163.com
Chenhui Jia
School ofMechatronical Engineering
University ofScience and Technology
Henan
Luoyang, Henan Province, China
xjiachenhui@163.com
Jianhai Han
School ofMechatronical Engineering
University ofScience and Technology
Henan
Luoyang, Henan Province, China
j ianhaihan@mail.haust.edu.cn
Abstract - An Unmanned bicycle stability adjusting mode by
use of parallel mechanism is presented, and dynamics model of
the unmanned bicycle with parallel mechanism adjusting
stability is upbuilt in this paper. In order to increase stability and
mobility, and carrying capability, the unmanned bicycle is
controlled by a pedalling torque, a directional torque that
generated using the steer adjustment, and by a tilting torque that
generated using a 2-RHR parallel mechanism mounted on the
crossbar, and then considering effects of all components of the
unmanned bicycle, and according to rolling without slipping
condition on two wheels on the ground, the kinematic constraints
and dynamics equations of the unmanned bicycle are set up more
fully and clearly than any of the existing models.
Index Terms - Unmanned bicycle, parallel mechanism,
stability adjustment, nonholonomic system, dynamics model.
I. INTRODUCTION
Bicycles have narrow bodies, and they have high
mobility, they have small turning radius. If such functions are
used efficiently, it is very possible and feasible that they are
applied in rescue operation at disasters or tasks in activities in
forests. The unmanned bicycle is a typical unstable system, its
dynamics, stability, and control are most important and
challenging research content, and arouse many scientists's
interest.
Bicycle stability problem has remained difficult to
analyze for decades, the main reason for this is the non-
availability of a mathmatical model that closely represents a
practical bicycle's dynamics. Existing models have lots of
approximations and assumptions, which drive them away from
the practical one. The works of Whipple [1], Klein and
Sommerfeld [2] had small-angle approximations. Jones [3]
and Le Henaff [4] concentrated on geometrical considerations
that neglected dynamical forces on the steering system. Franke
et.al [5] derived non-linear equations of motion of a rigid-rider
bicycle system using Newtonian mechanics. Hand [6]
developed the linearized equations of motion for general
bicycle geometry and obtained ranges of stable motion
depending on the velocity and parameters of the bicycle. In
their recent work on the same problem, Sharma et.al [7],[8]
developed a generalized bicycle model.
By far, bicycle mobility has not been brought into play,
one of reasons for this is that stability adjusting modes used do
not meet the mobility requirement. Getz [9] controlled bicycle
by use of adjusting steer and rear wheel. Yavin [10],[11]
controlled riderless bicycle by a pedalling torque, a directional
978-1-4244-2693-5/09/$25.00 2009 IEEE 1601
torque that generated using the steer adjustment, and by a
tilting torque that generated using a rotor or flywheel mounted
on the crossbar. Beznos [12] controlled two-wheel bicycle by
a pedalling torque, a directional torque that generated using
the steer adjustment, and by a tilting torque that generated
using a gyroscope mounted on the crossbar. Lee [13]
controlled unmanned electric bicycle by a pedalling torque, a
directional torque that generated using the steer adjustment,
and by a tilting torque that generated by moving transversely
a balance mass mounted on the crossbar. Yamakita [14] and
Lychek [15] controlled bicycle by a pedalling torque, a
directional torque that generated using the steer adjustment,
and by a tilting torque that generated by controlling a
pendulum mounted on the crossbar.
High stability and mobility are perfectly put up when a
human rider a bicycle, the main reason for this is that a human
body structure possesses multi-degree of freedom parallel
driving. Hence, simulating dynamics mechanism of human
riding bicycle, author brings forward a stability adjusting
method of unmanned bicycle to increase stabilizing and
carrying capability, that is, load is directly carried by parallel
mechanism, and then center of gravity of load can be directly
controlled by a 2-RHR parallel mechanism (Fig. 1). On the
other hand, the dynamics model is foundation of dynamics,
stability, and control research on the unmanned bicycle. Any
of the existing models of unmanned bicycle is approximate
and unclear. So, Based on multi-body system kinematic and
dynamics, author deduces detailedly holonomic and
nonholonomic constraints and dynamics equations to lay a
foundation for its dynamics, stability, and control research.
II. KINEMATIC CONSTRAINTS
In the paper, it is assumed that the ground is flat, inter
friction in the bicycle and wind resistance are negligible. In
order to set up the kinematic and dynamics model, inertia
reference frame and kinetic reference frames of the bicycle are
defined as follow, the origin of inertia reference frame {O} is
uniform with contact ground point of the rear wheel at starting
time, the z, axis is vertical to the ground and points up, the
X
o
axis is tangent to the rear wheel circumference and points
forwards. The origin of reference frame {I} fixed to the front
wheel locates at circle centre of the front wheel, the z, axis
points to its contact ground point at starting time, the Y1 axis is
along front wheel axis and points left.The origin of reference
frame {2} fixed to the steer locates at intersection point of the
steer axis and the crossbar, the Z2 axis is along steer axis and
down, the Y2axis points left at starting time. The origin of
reference frame {3} fixed to the crossbar locates at circle
centre of the rear wheel, the Z3axis is vertical to the crossbar
and points up, the Y3axis is along the rear wheel axis and
points left. The origin of reference frame {4} fixed to the steer
locates at circle centre of the rear wheel , the Z4 axis points to
its contact ground point at starting time, the Y4 axis is along
the rear wheel axis and points left.
/' J. /
parall el
front whee l I
Fig.l The unmanned bicycle
,
,
ta:
f:
: :
, ,
, ,
, ,
, ,
\ i rear wheel 4
Zo
Yo
Motion generated coordinates matrix of the bicycle are
defined as
q = [x
3
, Y3' Z3' a, .0, r, o, tp,;, If/p If/
2,
u, w, B]T (1)
Where
x
3
, Y 3 , Z 3 ,a ,.0 , rare location and posture parameters of
reference frame {3} fixed to the crossbar in inertia reference
frame {a},
1J is steering angle relative to the crossbar,
rp is rotation angle of the front wheel relative to the
crossbar,
; is the rear wheel rotation angle relative to the crossbar,
If/I is the left branch bar rotation angle of the parallel
mechanism relative to the crossbar,
If/2 is the right branch bar rotation angle of the parallel
mechanism relative to crossbar,
8
1
is the left branch bar changed length,
8
2
is left branch bar changed length,
u , w is motion platform displacement of the parallel
mechanism,
Bis motion platform rotation angle.
Unit vector d
1
along the axis of the front wheel is given
by
1602
d
l
o =[x
o'
Yo, zo] (!J.(z, r)!J.(y,{J)!J.(x, a)!J.(y,1[- r;)!J.(z, lJ)[O,I,O]T)
(2)
Contact ground unit vector of the front wheel is given by
t
l
O = (zo x dlo) x d
l
o=[xo,Yo ,zo] (3)
. (!i(z, r)fi(y,.o)fi(x, a)fi(y,1[- ';)!i(z, tJ)fi(y, G")[O,O,I]T)
from (3), angle G" between the contact ground vector t
1
and
the steer axis is obtained.
Vector Ttl of contaction ground point II in inertia reference
frame is denoted by
Ttl = [xo,Yo,zo]'!:tI (4)
here !:tI is given by
[r;'j =lFJz,";: Jl!!(y,"-:)!!(Z,&) 1
W1
(5)
(9)
(11)
(22)
(17)
- sin 0
cosO
o
[
COSO
==
=!i(z, r)!i(y, !3)!i(x, a)
COS(Jr-V/J -sin(Jr-V/z) %[L+t5
2
]
sin(ll"- /2) cos(ll"- /2) 0
1 1
(18)
where Ii ( i = 1,2,3,4 )denotes the moment of inertia of the
component of the bicycle parts, m
i
denotes the mass of the
component of the bicycle parts.
In (18),
where
a is length of motion platform of the parallel mechanism,
b is length of base support, L is initial length of branch bar,
H = -(a-b)2 .
III. DYNAMICS MODEL
The total kinetic energy T of the bicycle is given by
T
(1 T 1.T. ) 1 T ( )
= -OJ. I.OJ. +-mr. r . +-OJ
L
IdfT +1 L OJ
L
i=1 2 -I -I-I 2 I-IC-IC 2 - - L -u -
1 T (I I) 1 TIl . T .
+-OJ + OJ +-OJ OJ +-m r r
2 -R -dR -uR -R 2 -m-m-m 2 dL-dLc -dLc
1 .T. 1 .T. 1 .T. 1 .T .
+"2muL[.uLc[.uLc + "2m dR[.dRc[.dRc + "2m uR[.uRc[.uRc +"2
m m[.m[.m
(19)
_11_ 1_
which is the symmetrical matrix of the velocity of the
component of the bicycle parts, here is the orientation
matrix of the front wheel, and is given by
= !i(z, r)!i(y, !3)!i(x, a)!i(y, ll" - iJ)!i(y, rp) (20)
is the orientation matrix of the steer, and is given by
= !i(z, iJ) (21)
is the orientation matrix of the crossbar, and is given by
is the orientation matrix ofthe rear wheel, and is given by
= !i(z, r)!i(y,!3)!i(x,a)B.cy,) (23)
In (18), is vector of mass centre of the front wheel, and is
given by
(10)
(13)
Contact ground normal vector n, of the rear wheel is given by
x
3
r
4
[ ] == BJz, r)BJy, fJ)B.(x, a) ;: K) (12)
1 1
Unit vector along the axis of the rear wheel is given by
= [xo,Yo,zo]' (!i(z, r)!i(y,/J)!i(x,a)[O,I,O]T)
Contact ground unit vector of the rear wheel is given by
1 =(z, x d ) x d =[X
o
, Yo, z, ]
. (!i(z, r)!i(y, !3)!i(x, a)!i(y, 1\)[I,O,O]T)
from (10), angle K between the contact ground vector 1
4
and
the crossbar is obtained.
Vector '14 of contaction ground point t 4 of the rear wheel in
inertia reference frame is denoted by
'14 =[xo' Yo,Zo]
here r14 is given by
where r
4
is radius of the rear wheel.
Contact ground tangent vector T4 of the rear wheel is given by
T
4
n, =Z
oXT4
(14)
According to rolling without slipping condition of the rear
wheel, a holonomic constraint and two nonholonomic
constraints of the rear wheel is obtained by
'14 . z, =' '14' T4 =' '14' n4 =0 (15)
Also, two holonomic constraints of parallel mechanism which
contain four constraint equations is obtained by
-t
where 1
3
is length of the crossbar, 1
2
is length of the steer bar,
r
l
is radius of front wheel.
Contact ground tangent vector T
I
of the front wheel is given
by
T
I
=d
l
O
xz, (6)
Contact ground normal vector n
l
of the front wheel is given by
n
l
=ZoXT
I
(7)
According to rolling without slipping condition of the front
wheel, a holonomic constraint and two nonholonomic
constraints of the front wheel is obtained by
'tl .z, =0 ' 'tl' TI =0 ' 'tl' nl = (8)
(16)
1603
x
3
B.cz,r)B.cy,fJ)!i(x,a) Y3
o
/3 0
x !iCY, lC - ;)!i(z, 13) 0 0
o /2
o 1 1
r.2e is vector of mass centre of the steer, and is given by
x
3
Blz,Y)Bly,p)!l(x,a)
o 1
(24)
x
3
P3 0
== !l(z, Y)!l(y,P)!l(x, a) !l(X,Jr-lf/l)
o 1 0 1 1
(34)
r.uLe is vector of mass centre of the left up branch bar of the
parallel mechanism, and is given by
X3 P3
== !l(z, Y)!l(y,P)!l(x, a) !l(X,Jr-lf/l)
o 1 0 1
o
!..3e is vector of mass centre of the crossbar, and is given by
/3
0
(25)
x !i(y,lC-;)!i(Z,13) 0
0
0
C
2
0 1
r.4e is vector of mass centre of the rear wheel, and is given by
t : =[X
3'Y3,Z3]T
(27)
where C
2
denotes location of the mass centre of the steer,
C
3
denotes location of the mass centre of the crossbar.
In (18),
(38)
The total potential energy V of the bicycle is given by
4
V =LVi +V
dL
+V
uL
+V
dR
+V
uR
-v, (39)
i=l
(37)
r.m is vector of mass centre of the motion platform of the
parallel mechanism, and is given by
X
3
P3 U
!l(z,Y)!l(y,p)!l(x,a) !l(X,lf/2) :
o 1 0 1 1
o
1
o
o
1
here Vi is the potential energy of the component of the bicycle
parts, and is given by
(35)
r.dRe is vector of mass centre of the right down branch bar of
the parallel mechanism, and is given by
X
3
P3 0
= !i(z, r)!i(y,fJ)!i(x,a) Y3 !i(X,lf/2) -b CdL
Z3 0 0
o 1 0 1 1
(36)
r.uRe is vector of mass centre of the right up branch bar of the
parallel mechanism, and is given by
X3 P3
== !l(z, Y)!l(y,p)!l(x,a) !l(X,lf/2) -Ob
o 1 0 1
(26)
o
o
1
x
3
c
3
]== !l(z, Y)!l(y, P)!l(x, a)
o 1
---- 0 -1
0.
e.=L!i L!i (28)
which is the symmetrical matrix of the velocity of the left
branch bar of the parallel mechanism, here
= !i(z, r)!i(y, fJ)!i(x, a)!i(x, lC -If/1) (29)
In (18),
---- 0 -1 0 .
r!!.R=R!i R!i (30)
which is the symmetrical matrix of the velocity of the right
branch bar of the parallel mechanism, here
=!i(z, r)!i(y,fJ)!i(x,a)!i(x,lf/2) (31)
In (18),
---- 0 R- 1 0 .
r!!.m=m- .s (32)
which is the symmetrical matrix of the velocity of the motion
platform of the parallel mechanism, here
ts=!i(z, r)!i(y, fJ)!i(x, a)!i(x, B) (33)
In (18), r.dLe is vector of mass centre of the left down branch
bar of the parallel mechanism, and is given by
1604
u, =[O,O,mjg]"!:jc (40)
VdL is the potential energy of the left down branch bar of the
parallel mechanism, and is given by
V
dL
=[0,0, mdLg] "!:dLc (41)
V
uL
is the potential energy of the left up branch bar of the
parallel mechanism, and is given by
V
uL
= [0,0, muLg] "i.: (42)
VdR is the potential energy of the right down branch bar of the
parallel mechanism, and is given by
V
dR
= [0,0, mdRg] "!:dRc (43)
V
uR
is the potential energy of the right up branch bar of the
parallel mechanism, and is given by
V
uR
=[0,0, muRg] "!:uRc (44)
Vm is the potential energy of the motion platform of the
parallel mechanism, and is given by
Vm=[0,0, mmg]"!:m (45)
The generalized force matrix Q is given by
=[0,0,0,0,0,0,1"13,0, 1",1"lf/1' 1"lf/2' F
81
, F
82
,0,0,0]T (46)
where,
1"13 is the torque applied to the steerl,
1" is the torque applied to the rear wheel,
1"lf/1 is the torque applied to the left branch bar,
1"lf/2 is the torque applied to the right branch bar,
F
81
is the force applied to the left branch,
F
82
is the force applied to the right branch.
Thus, by use of the first langrange' s equations, the following
equations are obtained
au+i{(dcI]A.}+i{(dnk]A }=Q.
dt dqj dqj dqj )=1 dqj } k=l dqj k 1
(i =1,2,...,16)
(47)
so, the holonomic and nonholonomic kinematic constraints
(8), (15) -(17), and equation (47) constitute the dynamics
model of the unmanned bicycle.
IV. CONCLUSION
In the paper, the unmanned bicycle is controlled by a
pedalling torque, a directional torque that generated using the
steer adjustment, and by a tilting torque that generated using a
2-RHR parallel mechanism mounted on the crossbar. On the
other hand, considering effects of all components of the
unmanned bicycle, and according to rolling without slipping
condition on two wheels on the ground, the kinematic
constraints and dynamics equations of the unmanned bicycle
are set up more fully and clearly than any of the existing
models, so these works lays a foundation for dynamics,
stability and control research on unmanned bicycle.
1605
REFERENCES
[1] F.1. W. Whipple, "The Stability of the Motion of a Bicycle," Quarterly
Journal of Pure and Applied Mathematics, 30(120), 1899, pp. 312-348.
[2] F. Klein and A. Sommerfeld, "Uber die Theorie des Kreisels," Teubner
Verlag Stuttgart, 1965.
[3] D. H. Jones, "The Stability of a Bicycle," Physics Today, 23(4),1970, pp.
34-40.
[4] Y. Le Henaff, "Dynamic Stability of the Bicycle," European Journal of
Physics, 8, 1987, pp. 207-210.
[5] G. Franke, W. Suhr and F. RieB, "An Advanced Model of Bicycle,"
European Journal of Physics, 11, 1990, pp. 116-121.
[6] R. S. Hand, "Comparisons and Stability Analysis of Linearized Equations
of Motion for a Basic Bicycle Model," PhD thesis, Cornell University,
1988.
[7] Himanshu Dutt Sharma, Sameer M. Kale, Umashankar N, "Simulation
Model for Studying Inherent Stability Characteristics of Autonomous
Bicycle," Proceedings of IEEE International Conference on
Mechatronics and Automation, Niagara Falls, Canada, July 2005.
[8] Himanshu Dutt Sharma, Umashankar N, "A Robotic Model (ROBI) of
Autonomous Bicycle System," Proceedings of IEEE International
Conference on Computational Intelligence for Modelling and Automation,
and International Conference on Intelligent Agents, Web Technologies
and Internet Commerce, Sydney, NSW, December 2006
[9] N. H. Getz, 1. E. Marsden, "Control for An Autonomous Bicycle,"
Proceedings of the 1995 IEEE International Conference on Robotics and
Automation, Nagoya, May 1995.
[IO]Y. Yavin, "Stabilization and Control of the Motion of an Autonomous
Bicycle by Using a Rotor for the Tilting Moment," Computer Methods in
Applied Mechanics and Engineering, no. 178, pp. 233-243.
[Il]Y. Yavin, "Modelling and Control of The Motion of A Riderless Bicycle
Rolling on A Moving Plane," Computers and mathematics with
Applications, vol. 54, no. 11-12, pp. 1319-1328.
[12]A. V. Beznos, A. M. Formal'sky, E. V. Gurfinkel, D. N. Jicharev, A. V.
Lensky, K. V. Savitsky, L. S. Tchesalin, "Control of Autonomous Motion
of Two-wheel Bicycle with Gyroscopic Stabilization," Proceedings of
IEEE International Conference on Robotics and Automation, Leuven,
Belgium, May 1998.
[13]S. Lee, W. Ham, "Self Stabilizing Strategy in Tracking Control of
Unmanned Electric Bicycle with Mass Balance," Proceedings of the 2002
IEEE/RSJ International Conference on Intelligent Robots and Systems,
EPFL, Lausanne, Switzerland, October 2002.
[14]M. Yamakita, A. Utano, K. Sekiguchi, "Experimental Study of Automatic
Control of Bicycle with Balancer," Proceedings of the 2006 IEEE/RSJ
International Conference on Intelligent Robots and Systems, Beijing,
China, October 2006.
[15]K. Lychek, M. Yamakita, "Trajectory control for an autonomous bicycle
with balancer," Proceedings of the 2008 IEEE/ASME International
Conference on Advanced Intelligent Mechatronics, Xi'an, China, July
2008.
Anda mungkin juga menyukai
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDari EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifePenilaian: 4 dari 5 bintang4/5 (5794)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDari EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You ArePenilaian: 4 dari 5 bintang4/5 (1090)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDari EverandNever Split the Difference: Negotiating As If Your Life Depended On ItPenilaian: 4.5 dari 5 bintang4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDari EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RacePenilaian: 4 dari 5 bintang4/5 (894)
- Grit: The Power of Passion and PerseveranceDari EverandGrit: The Power of Passion and PerseverancePenilaian: 4 dari 5 bintang4/5 (587)
- Shoe Dog: A Memoir by the Creator of NikeDari EverandShoe Dog: A Memoir by the Creator of NikePenilaian: 4.5 dari 5 bintang4.5/5 (537)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDari EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FuturePenilaian: 4.5 dari 5 bintang4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDari EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersPenilaian: 4.5 dari 5 bintang4.5/5 (344)
- Her Body and Other Parties: StoriesDari EverandHer Body and Other Parties: StoriesPenilaian: 4 dari 5 bintang4/5 (821)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Dari EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Penilaian: 4.5 dari 5 bintang4.5/5 (119)
- The Emperor of All Maladies: A Biography of CancerDari EverandThe Emperor of All Maladies: A Biography of CancerPenilaian: 4.5 dari 5 bintang4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingDari EverandThe Little Book of Hygge: Danish Secrets to Happy LivingPenilaian: 3.5 dari 5 bintang3.5/5 (399)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDari EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyPenilaian: 3.5 dari 5 bintang3.5/5 (2219)
- The Yellow House: A Memoir (2019 National Book Award Winner)Dari EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Penilaian: 4 dari 5 bintang4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDari EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaPenilaian: 4.5 dari 5 bintang4.5/5 (265)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDari EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryPenilaian: 3.5 dari 5 bintang3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnDari EverandTeam of Rivals: The Political Genius of Abraham LincolnPenilaian: 4.5 dari 5 bintang4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealDari EverandOn Fire: The (Burning) Case for a Green New DealPenilaian: 4 dari 5 bintang4/5 (73)
- The Unwinding: An Inner History of the New AmericaDari EverandThe Unwinding: An Inner History of the New AmericaPenilaian: 4 dari 5 bintang4/5 (45)
- Rise of ISIS: A Threat We Can't IgnoreDari EverandRise of ISIS: A Threat We Can't IgnorePenilaian: 3.5 dari 5 bintang3.5/5 (137)
- C680Dokumen22 halamanC680dinhtung2210100% (2)
- Composites of Polymer and Orange PeelDokumen7 halamanComposites of Polymer and Orange PeelkarthiBelum ada peringkat
- Conduction, Convection, & RadiationDokumen14 halamanConduction, Convection, & Radiationyuvionfire100% (1)
- Microplan - Katalog 2016 ENDokumen55 halamanMicroplan - Katalog 2016 END.T.Belum ada peringkat
- AASHTO Guide Specifications For Design of Pedestrian Bridges 2009 (Draft)Dokumen17 halamanAASHTO Guide Specifications For Design of Pedestrian Bridges 2009 (Draft)Laurence Arcon Banal0% (1)
- Lucia 1995 Rock-FabricPetrophysical Classification of Carbonate Pore SpaceDokumen26 halamanLucia 1995 Rock-FabricPetrophysical Classification of Carbonate Pore SpaceMarcos Antonio Romero Arteaga100% (1)
- Astm D 3612 - 01Dokumen24 halamanAstm D 3612 - 01mtuankctBelum ada peringkat
- Iisus A Fost Crucificat La Constantinopole Si Nu La Ierusalim - Partea IVDokumen65 halamanIisus A Fost Crucificat La Constantinopole Si Nu La Ierusalim - Partea IVsando khanBelum ada peringkat
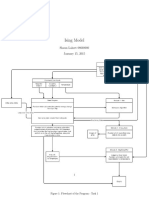
- Ising ModelDokumen5 halamanIsing Modeldecerto252Belum ada peringkat
- Reka Bentuk, Pembinaan Dan Pentadbiran UjianDokumen9 halamanReka Bentuk, Pembinaan Dan Pentadbiran UjianAiman HazimBelum ada peringkat
- Gear Motors: Achieving The Perfect Motor & Gearbox MatchDokumen16 halamanGear Motors: Achieving The Perfect Motor & Gearbox MatchJohn LeeBelum ada peringkat
- POMFriction AssessmentDokumen11 halamanPOMFriction AssessmentJoãoAraújoBelum ada peringkat
- IEEE Paper For Image ProcessingDokumen32 halamanIEEE Paper For Image Processingsaravanan_dijucsBelum ada peringkat
- Stepper Motor Driven Solar Tracker SystemDokumen4 halamanStepper Motor Driven Solar Tracker SystemFAHMY RINANDA SAPUTRI (066629)Belum ada peringkat
- Venturi and Orifice Volumetric Flow Measure-MentDokumen4 halamanVenturi and Orifice Volumetric Flow Measure-Mentmuiz_jojoBelum ada peringkat
- Standing Waves On A StringDokumen6 halamanStanding Waves On A StringamirpouyanBelum ada peringkat
- Schlumberger Log Interpretation ChatsDokumen287 halamanSchlumberger Log Interpretation ChatsSabrianto AswadBelum ada peringkat
- SosthenesDokumen396 halamanSosthenesAthiesh KumarBelum ada peringkat
- TMTL2400KDokumen4 halamanTMTL2400KRushit ShahBelum ada peringkat
- CE 3310 Assignment 2Dokumen1 halamanCE 3310 Assignment 2SSBelum ada peringkat
- PMM WordDokumen3 halamanPMM WordShrey R DhanawadkarBelum ada peringkat
- Cem - Part 1 PDFDokumen19 halamanCem - Part 1 PDFDavin OtogleBelum ada peringkat
- 06 Slewing PDFDokumen14 halaman06 Slewing PDFJuan Alberto Giglio FernándezBelum ada peringkat
- P Ractical Approaches To Fast Gas Chromatography-Mass Spectrometry Muy BuenoDokumen28 halamanP Ractical Approaches To Fast Gas Chromatography-Mass Spectrometry Muy BuenoJavier Joao Lloyd IglesiasBelum ada peringkat
- Steam Drum Design CalsDokumen78 halamanSteam Drum Design Calsabdulrehmandescon100% (1)
- Gujarat Technological University: W.E.F. AY 2018-19Dokumen3 halamanGujarat Technological University: W.E.F. AY 2018-19SURAJ NAKUMBelum ada peringkat
- Xxii Paper 51Dokumen9 halamanXxii Paper 51kjyeom_258083906Belum ada peringkat
- Working of Steam Turbines and Its AuxillariesDokumen48 halamanWorking of Steam Turbines and Its AuxillariesbalajigandhirajanBelum ada peringkat
- (Architecture Ebook) Alvar Aalto, Alvar Aalto and The Bio-ArchitectureDokumen5 halaman(Architecture Ebook) Alvar Aalto, Alvar Aalto and The Bio-Architecturepooh86poohBelum ada peringkat
- Chapter 3 Linear KinematicsDokumen26 halamanChapter 3 Linear KinematicsKuldeep SinghBelum ada peringkat