APPLIED PHYSICS LETTERS

VOLUME 73, NUMBER 23

7 DECEMBER 1998

Optical engineering with Fibonacci dielectric multilayers

Enrique Maciaa)
GISC, Departamento de Fsica de Materiales, Facultad de Fsicas, Universidad Complutense, E-28040 Madrid, Spain

Received 27 July 1998; accepted for publication 5 October 1998 We study the resonant transmission of light through Fibonacci dielectric multilayers FDM . Making use of a transfer matrix renormalization technique E. Macia and F. Domnguez-Adame, Phys. Rev. Lett. 76, 2957 1996 we obtain closed analytical expressions for the transmission coefcient under arbitrary incidence angle conditions. We analyze the relationship between the resonant wavelengths and the quasiperiodic structure of the substrate, suggesting the potential use of arrays containing FDMs of different sizes in the design of optical microcavities. 1998 American Institute of Physics. S0003-6951 98 02249-9

During the last decade the notion of quasiperiodic order has considerably evolved, opening promising avenues in the physics of condensed matter. At the beginning, quasiperiodic systems were mainly considered as suitable theoretical models to describe the conceptual transition from randomness to periodic order. Later, it was progressively realized that deterministically ordered aperiodic structures may offer interesting possibilities for technological applications as well. Thus, x-ray diffraction studies1 demonstrated that, in quasiperiodic heterostructures, two kinds of order coexist in the same sample at different length scales, a feature distinguishing them from usual periodic multilayers. In fact, at the atomic level we have the usual periodic order determined by the crystalline arrangement of atoms in each layer; but, at longer scales (10 102 nm), we have the quasiperiodic order determined by the sequential deposition of the different layers. This long-range aperiodic order is articially imposed during the system growth process and can be precisely controlled. Since different physical phenomena have their own relevant physical scales, by properly matching the characteristic length scales of elementary excitations propagating through the system, we can probe the physical properties related to the aperiodic order we have introduced in the system. In this way, Diez et al. have shown that Fibonacci superlattices based on GaAsGaAlAs can act as efcient electronic lters.2 However, in order to fully appreciate specic features of quasiperiodic systems, arising from the fractal nature of their energy spectra3 and the critical nature of their states,4,5 the study of classical waves has a number of advantages over the study of quantum elementary excitations since, in this case, the presence of electronphonon, electronelectron, or spin-orbit interactions analysis of data difcult. Accordingly, a number of experimental studies dealing with the propagation of third sound6 and ultrasonic waves7 in Fibonacci multilayers have been reported, conrming that characteristic self-similar features in the transmission spectra are observable when long-range aperiodic modulation is established at the micrometer range. In the same line, the introduction of the Fibonacci dielectric multia

layers FDM by Kohmoto et al.8 spurred interest both for the possible optical applications9 and theoretical aspects of light transmission in aperiodic media,10,11 pointing towards the possible localization of light by the effect of the quasiperiodic order.12 In this letter we provide further evidence of the rich behavior of light propagating through quasiperiodic media by obtaining general analytical expressions for the transmission coefcient in FDMs which allow us to study the relationship between the resonant wavelengths and the quasiperiodic structure of the substrate. Based on the obtained results we suggest the use of sandwiched arrays of FDMs to design optical microcavities of practical interest. To this end we study the transmission of light through a FDM consisting of two kinds of layers, labeled A and B, which are arranged according to the Fibonacci sequence, obeying the concatenation rule S j 1 S j 1 S j , for j 1, with S 0 B and S 1 A. 8 The resulting structure for S 4 is shown in Fig. 1 a . The number of layers is given by N F j , where F j is a Fibonacci number obtained from the recursive law F j 1 F j F j 1 , with F 1 1 and F 0 1. When studying the propagation of light in multilayered systems one must consider the propagation across the interface separating two neighboring layers described by the matrices G i 1,i in Fig. 1 b along with the light propagation within each layer described by the matrices L i in Fig. 1 b . Within the transfer

Electronic mail: mat04@emducmsl.sis.ucm.es 3330

FIG. 1. Sketch illustrating the propagation of light through a the quasiperiodic S 4 FDM, b the sequence of G i 1,i and L i auxiliary matrices, c the sequence of light transfer matrices K i 1,i , and d the renormalization scheme for the transfer matrices proposed in this work. 1998 American Institute of Physics

0003-6951/98/73(23)/3330/3/$15.00

Downloaded 19 Apr 2012 to 200.17.143.33. Redistribution subject to AIP license or copyright; see http://apl.aip.org/about/rights_and_permissions

Appl. Phys. Lett., Vol. 73, No. 23, 7 December 1998

Enrique Macia

3331

matrix formalism the transmission of light through the entire multilayer can be properly described in terms of the matrices see Fig. 1 c cos K AA G AA L A sin
A A B B

sin cos

A A

,
B B

cos K AB G AB L B u
1

sin u sin u cos

1

sin
A A

cos
A A

Taking into account commutation conditions ii and iii we are led to consider three different possible situations. a The case A B n , which implies n A d A n B d B , has been previously considered in a number of works810,12 usually restricting to the normal incidence ( 1) geometry .15 In this case the half-wavelength condition is satised at every layer. Therefore, Q A I and Q B ( 1) n I, where I denotes the identity matrix, and the transparency condition, T 1, is trivially obtained. b The case B n , for which the global transfer matrix has the form M N 1
np

cos K BA G BA L A u sin

cos sin

sin cos , 4

where i n i d i k/cos i , n i are the refractive indices, d i are the widths of the layers, k is the wave vector in vacuum, i are the incidence angles, and we have dened u R with cos A /cos B 0. Therefore, to obtain the R n A /n B and global transfer matrix, we must evaluate a matrix product involving three different types of transfer matrices which, in addition, are ordered quasiperiodically. At this point, we shall take advantage of the transfer matrix renormalization technique recently introduced by us5,13 to obtain an analytical expression for the transmission coefcient of light propagating in a FDM. The key point of our approach consists of renormalizing the set of transfer matrices K i 1,i according to the blocking scheme Q B K AA and Q A K AB K BA illustrated in Fig. 1 d . Note that the renormalized transfer matrix sequence is also arranged according to the Fibonacci sequence and, consequently, the topological order present in the original FDM is preserved by the renormalization process. Now, we realize that the matrices Q A and Q B are unimodular i.e., their determinant is unity for any choice of the system parameters and for any value of the light wavelength; and that the Q i matrices commute under certain circumstances. In fact, after some algebra we get cos Q A ,Q B where J
A, B

A, B

A A

sin cos

A A

sin

u2 1 sin u

sin

B.

The commutator 2 vanishes in three different cases (u 0): i The choice u 1, which reduces to the trivial periodic case n A n B , and the choices ii A n , and iii B n , with n 1,2,... . Therefore, in order to satisfy the commutation condition 2 , it is not necessary to impose restrictive conditions onto both kinds of layers simultaneously. For those wavelengths verifying the condition Q A ,Q B 0, we can express the global transfer matrix of the system p as M (N) Q A Q q , where p F j 2 and q F j 3 . Note that B for a FDM of length N, p indicates the number of B layers present in the system. Then, making use of the Cayley Hamilton theorem for unimodular matrices,14 the matrix M (N) can be explicitly evaluated in terms of Chebyshev polynomials of the second kind. From the knowledge of M (N) the transmission coefcient can be obtained from the standard expression T 4/( M (N) 2), where M (N) denotes the sum of the squares of the four elements of the global transfer matrix.

where n(p q) Rd A / d B . In this case, we get T 1 for any as well. Physically, this result can be easily interpreted if we keep in mind that when the B layers satisfy the half-wavelength condition, the transmission properties of the FDM will depend entirely on the interaction of light with the layers of material A. Now, since the optical behavior of the double layers AA is completely equivalent to that of single A layers (G AA I) and, according to the Fibonacci sequence, B layers always appear anked by A layers, those wavelengths satisfying the resonance condition n 2n B d B , will effectively see a periodic distribution of A layers separated by fully transparent slabs of constant width d B . In this case the two-component FDM will behave like an equivalent homogeneous periodic medium, characterized by an effective thickness d (p q)d A , and a refraction index n A . Note that, if instead of imposing the half-wavelength condition onto the B layers, we make the substitution BA, replacing all the B type layers originally present in the FDM by type A ones, we should obtain a homogenous system of length Nd A d . Consequently, the FDM will exhibit an effective optical phase shrinkage for those wavelengths satisfying the resonance condition. Interestingly, a similar behavior has been recently reported in photonic crystals with correlated disorder.16 This physical scenario changes substantially if we impose condition c A n . In this case, the layers of material A become fully transparent to the incoming light and, consequently, the transmission properties of the FDM will depend on the interaction of light with the layers of material B. The key point now is to realize that these layers are spaced by two different distances, d A and d AA 2d A , arranged according to a quasiperiodic sequence. Hence, those wavelengths satisfying the resonance condition n 2n A d A , will effectively see a quasiperiodic distribution of B layers, instead of a periodic one. The explicit evaluation of the transmission coefcient leads to T 1 1 , u2 1 2 2 sin p 2u 5

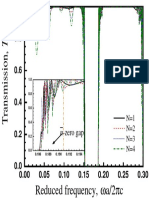
n /R and d B /d A . Although expression where 5 is completely general, for the sake of illustration, we shall consider that A B layers are composed of SiO2 (TiO2) whose indices of refraction at 700 nm are n A 1.45 and n B 2.30, respectively. In Fig. 2 we show the dependence of the transmission coefcient with for three FDMs containing N 5, N 8 and N 13 layers, under normal incidence

Downloaded 19 Apr 2012 to 200.17.143.33. Redistribution subject to AIP license or copyright; see http://apl.aip.org/about/rights_and_permissions

3332

Appl. Phys. Lett., Vol. 73, No. 23, 7 December 1998

Enrique Macia

FIG. 2. Dependence of the transmission coefcient with the design parameter , for n 1 and 1, corresponding to S 4 thick solid line , S 5 thin solid line , and S 6 dashed line FDMs. The inset shows a scheme for a FDM resonating microcavity.

conditions. By inspecting Fig. 2 we observe that the curves R T( ) are symmetrical with respect to the axis 1.5862 , and exhibit a series of maxima (T max 1) and 1 minima (T min 1 (u2 1)/2u 2 0.8140 1). The number of both maxima and minima increases as the FDM size increases, and their relative positions shift with respect to the symmetry axis. Physically, the origin for such oscillatory patterns can be understood as follows. Under the A layer resonance condition, which xes the value for the incoming light wavelength, the constructive or destructive nature of the interferences, arising from the interaction of light with the quasiperiodic distribution of B layers, will be strongly dependent on the precise relationship between and the structural R we get the wellparameters d A and d B . Thus, when known relationship n A d A n B d B , corresponding to the particular case where both A and B layers simultaneously satisfy the resonance condition. Interestingly, Fig. 2 shows that there exists a signicant number of additional values of for which the transparency (T 1) condition is satised in FDMs of variable length. Conversely, if we choose the value of in such a way that the wavelengths satisfying the resonant condition at the A layers verify the quarter-wavelength condition at the B layers, the quasiperiodic distribution of B layers efciently backscatter the incoming light, resulting in a signicant reduction of the transmission coefcient value. For any choice of the parameter other than those just described, the transmission coefcient will adopt different valcan be reues in the interval T min T 1. Accordingly, garded as a control design parameter able to determine the overall FDM optical behavior, varying from that corresponding to a selective lter (T 1) to that proper of a reective coating (T min). On the other hand, making use of the analytical expresR/2 or 3R/2 the transmission 5 we see that when

sion coefcient attains an extreme value, which should be a minimum or a maximum depending on the parity of the integer p: when p is even we get T 1, while for odd p we have T T min . Since the parity of the Fibonacci numbers exhibits the recurrence oddoddeven, the transmission coefcients corresponding to consecutive S j FDMs should alternate accordingly, as is illustrated in Fig. 2 for the FDMs corresponding to p 2, p 3, and p 5. This interesting property could be used to construct resonating optical cavities where an even FDM for instance, S 4 ), exhibiting full transmission, is sandwiched between two odd FDMs for instance S 5 ), behaving as optical mirrors. A sketch of such a dispositive is shown as an inset in Fig. 2. In summary, making use of our transfer matrix renormalization technique, we obtain analytical expressions for the transmission coefcient of light propagating through a FDM with arbitrary angle incidence conditions. Then, we probe the quasiperiodic order of the system by properly matching the wavelength of the incoming light with the design parameter , suggesting the possibility of constructing resonating optical devices that exploit the interference possibilities associated with the quasiperiodic order of the substrate. I would like to thank Francisco Domnguez-Adame, Jonn Rams, and Victoria Hernandez for useful comments. gu
R. Merlin, K. Bajema, R. Clarke, F. Y. Juang, and P. K. Bhattacharya, Phys. Rev. Lett. 55, 1768 1985 ; J. Todd, R. Merlin, R. Clarke, K. M. Mohanty, and J. D. Axe, ibid. 57, 1157 1986 . 2 E. Diez, F. Domnguez-Adame, E. Macia, and A. Sanchez, Phys. Rev. B 54, 16792 1996 . 3 A. Suto, J. Stat. Phys. 56, 525 1989 ; J. Bellissard, B. Iochum, E. Scop pola, and D. Testard, Commun. Math. Phys. 125, 527 1989 ; E. Macia and F. Domnguez-Adame, Semicond. Sci. Technol. 11, 1041 1996 . 4 S. Ostlund and R. Pandit, Phys. Rev. B 29, 1394 1984 ; M. Kohmoto, B. Sutherland, and C. Tang, ibid. 35, 1020 1987 . 5 E. Macia and F. Domnguez-Adame, Phys. Rev. Lett. 76, 2957 1996 . 6 K. Kono, S. Nakada, Y. Narahara, and Y. Ootuka, J. Phys. Soc. Jpn. 60, 368 1991 . 7 Y. Zhu, N. Ming, and W. Jiang, Phys. Rev. B 40, 8536 1989 . 8 M. Kohmoto, B. Sutherland, and K. Iguchi, Phys. Rev. Lett. 58, 2436 1987 . 9 C. Schwartz, Appl. Opt. 27, 1232 1988 . 10 R. Riklund and M. Severin, J. Phys. C 21, 3217 1988 ; M. Dulea, M. Severin, and R. Riklund, Phys. Rev. B 42, 3680 1990 ; H. Miyazaki and M. Inoue, J. Phys. Soc. Jpn. 59, 2536 1990 ; N. H. Liu, Phys. Rev. B 55, 3543 1997 . 11 A. Latge and F. Claro, Opt. Commun. 94, 389 1992 ; M. S. Vasconcelos, E. L. Albuquerque, and A. M. Mariz, J. Phys.: Condens. Matter 10, 5839 1998 . 12 W. Gellermann, M. Kohmoto, B. Sutherland, and P. C. Taylor, Phys. Rev. Lett. 72, 633 1994 ; T. Hattori, N. Tsurumachi, S. Kawato, and H. Nakatsuka, Phys. Rev. B 50, 4220 1994 . 13 E. Macia, Phys. Rev. B 57, 7661 1998 . 14 See, for example, J. M. Luck, in Fundamental Problems in Statistical Mechanics VIII Elsevier, New York, 1994 . 15 A detailed account on the light propagation in FDM as a function of the incidence angle is given in Ref. 11. 16 X. Y. Lei, H. Li, F. Ding, W. Zhang, and N. B. Ming, Appl. Phys. Lett. 71, 2889 1997 .
1

Downloaded 19 Apr 2012 to 200.17.143.33. Redistribution subject to AIP license or copyright; see http://apl.aip.org/about/rights_and_permissions