Bivariate
Diunggah oleh
Vikas SainiDeskripsi Asli:
Judul Asli
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Bivariate
Diunggah oleh
Vikas SainiHak Cipta:
Format Tersedia
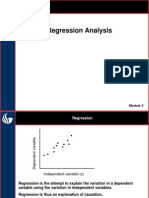
Bivariate analysis
The Multiple Regression Model
Idea: Examine the linear relationship between
1 dependent (Y) & 2 or more independent variables (X
i
)
i ki k 2i 2 1i 1 0 i
X X X Y + + + + + =
Multiple Regression Model with k Independent Variables:
Y-intercept
Population slopes Random Error
Assumptions of Regression
Use the acronym LINE:
Linearity
The underlying relationship between X and Y is linear
Independence of Errors
Error values are statistically independent
Normality of Error
Error values () are normally distributed for any given value of X
Equal Variance (Homoscedasticity)
The probability distribution of the errors has constant variance
Regression Statistics
Multiple R 0.998368
R Square 0.996739
Adjusted R
Square 0.995808
Standard
Error 1.350151
Observations 28
ANOVA
df SS MS F
Significan
ce F
Regression 6 11701.72 1950.286 1069.876 5.54E-25
Residual 21 38.28108 1.822908
Total 27 11740
.996739
11740
11704.1
SST
SSR
r
2
= = =
99.674% variation is
explained by the
dependent Variables
Adjusted r
2
r
2
never decreases when a new X variable is
added to the model
This can be a disadvantage when comparing models
What is the net effect of adding a new variable?
We lose a degree of freedom when a new X variable
is added
Did the new X variable add enough explanatory
power to offset the loss of one degree of freedom?
Shows the proportion of variation in Y explained
by all X variables adjusted for the number of X
variables used
(where n = sample size, k = number of independent variables)
Penalize excessive use of unimportant independent
variables
Smaller than r
2
Useful in comparing among models
Adjusted r
2
(
|
.
|
\
|
=
1
1
) 1 ( 1
2 2
k n
n
r r
adj
Error and coefficients relationship
B1 = Covar(yx)/Varp(x)
Stddevp 419.28571 1103.4439 115902.4 1630165.82 36245060.6 706538.59 195.9184
Covar 662.14286 6862.5 25621.4286 120976.786 16061.643 257.1429
b1 0.6000694 0.059209 0.01571707 0.00333775 0.0227329 1.3125
Is the Model Significant?
F Test for Overall Significance of the Model
Shows if there is a linear relationship between all of the
X variables considered together and Y
Use F-test statistic
Hypotheses:
H
0
:
1
=
2
= =
k
= 0 (no linear relationship)
H
1
: at least one
i
0 (at least one independent
variable affects Y)
F Test for Overall Significance
Test statistic:
where F has (numerator) = k and
(denominator) = (n k - 1)
degrees of freedom
1 k n
SSE
k
SSR
MSE
MSR
F
= =
Case discussion
Multiple Regression Assumptions
Assumptions:
The errors are normally distributed
Errors have a constant variance
The model errors are independent
e
i
= (Y
i
Y
i
)
<
Errors (residuals) from the regression model:
Error terms and coefficient estimates
Once we think of the Error term as a random
variable, it becomes clear that the estimates
of b1, b2, (as distinguished from their true
values) will also be random variables, because
the estimates generated by the SSE criterion
will depend upon the particular value of e
drawn by nature for each individual in the
data set.
Statistical Inference and Goodness of
fit
The parameter estimates are themselves random
variables, dependent upon the random variables e.
Thus, each estimate can be thought of as a draw
from some underlying probability distribution, the
nature of that distribution as yet unspecified.
If we assume that the error terms e are all drawn
from the same normal distribution, it is possible to
show that the parameter estimates have a normal
distribution as well.
T Statistic and P value
T = B1-B1average/B1 std dev
Can you have a hypothesis that
b1 average = b1 estimate
and do the T test
Are Individual Variables Significant?
Use t tests of individual variable slopes
Shows if there is a linear relationship between the
variable X
j
and Y
Hypotheses:
H
0
:
j
= 0 (no linear relationship)
H
1
:
j
0 (linear relationship does exist
between X
j
and Y)
Are Individual Variables Significant?
H
0
:
j
= 0 (no linear relationship)
H
1
:
j
0 (linear relationship does exist
between x
j
and y)
Test Statistic:
(df = n k 1)
j
b
j
S
b
t
0
=
Coefficien
ts
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept -59.0661 11.28404 -5.23448 3.45E-05 -82.5325 -35.5996 -82.5325 -35.5996
OFF -0.00696 0.04619 -0.15068 0.881663 -0.10302 0.089097 -0.10302 0.089097
BAR 0.041988 0.005271 7.966651 8.81E-08 0.031028 0.052949 0.031028 0.052949
YNG 0.002716 0.000999 2.717326 0.012904 0.000637 0.004794 0.000637 0.004794
VEH 0.00147 0.000265 5.540878 1.69E-05 0.000918 0.002021 0.000918 0.002021
INV -0.00274 0.001336 -2.05135 0.052914 -0.00552 3.78E-05 -0.00552 3.78E-05
SPD -0.2682 0.068418 -3.92009 0.000786 -0.41049 -0.12592 -0.41049 -0.12592
with n (k+1) degrees of freedom
Confidence Interval Estimate
for the Slope
Confidence interval for the population slope
j
where t has (n k 1) d.f.
j
b k n j
S t b
1
Example: Form a 95% confidence interval for the effect of
changes in Bars on fatal accidents:
0.041988 (2.079614 )(0.005271)
So the interval is (0.031028, 0.052949 )
(This interval does not contain zero, so bars has a significant
effect on Accidents)
Coefficien
ts
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Intercept -59.0661 11.28404 -5.23448 3.45E-05 -82.5325 -35.5996
OFF -0.00696 0.04619 -0.15068 0.881663 -0.10302 0.089097
BAR 0.041988 0.005271 7.966651 8.81E-08 0.031028 0.052949
YNG 0.002716 0.000999 2.717326 0.012904 0.000637 0.004794
VEH 0.00147 0.000265 5.540878 1.69E-05 0.000918 0.002021
INV -0.00274 0.001336 -2.05135 0.052914 -0.00552 3.78E-05
SPD -0.2682 0.068418 -3.92009 0.000786 -0.41049 -0.12592
Using Dummy Variables
A dummy variable is a categorical explanatory
variable with two levels:
yes or no, on or off, male or female
coded as 0 or 1
Regression intercepts are different if the
variable is significant
Assumes equal slopes for other variables
Interaction Between
Independent Variables
Hypothesizes interaction between pairs of X
variables
Response to one X variable may vary at different
levels of another X variable
Contains cross-product term
) X (X b X b X b b
X b X b X b b Y
2 1 3 2 2 1 1 0
3 3 2 2 1 1 0
+ + + =
+ + + =
Effect of Interaction
Given:
Without interaction term, effect of X
1
on Y is
measured by
1
With interaction term, effect of X
1
on Y is
measured by
1
+
3
X
2
Effect changes as X
2
changes
X X X X Y
2 1 3 2 2 1 1 0
+ + + + =
X
2
= 1:
Y = 1 + 2X
1
+ 3(1) + 4X
1
(1) = 4 + 6X
1
X
2
= 0:
Y = 1 + 2X
1
+ 3(0) + 4X
1
(0) = 1 + 2X
1
Interaction Example
Slopes are different if the effect of X
1
on Y depends on X
2
value
X
1
4
8
12
0
0 1 0.5 1.5
Y
= 1 + 2X
1
+ 3X
2
+ 4X
1
X
2
Suppose X
2
is a dummy variable and the estimated regression equation is
Y
Residual Analysis
The residual for observation i, e
i
, is the difference between
its observed and predicted value
Check the assumptions of regression by examining the
residuals
Examine for linearity assumption
Evaluate independence assumption
Evaluate normal distribution assumption
Examine for constant variance for all levels of X (homoscedasticity)
Graphical Analysis of Residuals
Can plot residuals vs. X
i i i
Y
Y e =
Residual Analysis for
Independence
Not Independent
Independent
X
X
r
e
s
i
d
u
a
l
s
r
e
s
i
d
u
a
l
s
X
r
e
s
i
d
u
a
l
s
Residual Analysis for
Equal Variance
Non-constant variance
Constant variance
x x
Y
x
x
Y
r
e
s
i
d
u
a
l
s
r
e
s
i
d
u
a
l
s
Linear fit does not give
random residuals
Linear vs. Nonlinear Fit
Nonlinear fit gives
random residuals
X
r
e
s
i
d
u
a
l
s
X
Y
X
r
e
s
i
d
u
a
l
s
Y
X
Quadratic Regression Model
Quadratic models may be considered when the scatter diagram takes on one of
the following shapes:
X
1
Y
X
1
X
1
Y Y Y
1
< 0
1
> 0
1
< 0
1
> 0
1
= the coefficient of the linear term
2
= the coefficient of the squared term
X
1
i
2
1i 2 1i 1 0 i
X X Y + + + =
2
> 0
2
> 0
2
< 0
2
< 0
Anda mungkin juga menyukai
- Chapter 14, Multiple Regression Using Dummy VariablesDokumen19 halamanChapter 14, Multiple Regression Using Dummy VariablesAmin HaleebBelum ada peringkat
- Simple Linear Regression GuideDokumen58 halamanSimple Linear Regression Guideruchit2809Belum ada peringkat
- Difference Equations in Normed Spaces: Stability and OscillationsDari EverandDifference Equations in Normed Spaces: Stability and OscillationsBelum ada peringkat
- Sonek Linear Regression NotesDokumen11 halamanSonek Linear Regression NotesAlfredBelum ada peringkat
- A-level Maths Revision: Cheeky Revision ShortcutsDari EverandA-level Maths Revision: Cheeky Revision ShortcutsPenilaian: 3.5 dari 5 bintang3.5/5 (8)
- Quantile RegressionDokumen43 halamanQuantile RegressionSavita KayBelum ada peringkat
- Trend Analysis-1Dokumen45 halamanTrend Analysis-1TauseefBelum ada peringkat
- Linear Regression and Correlation AnalysisDokumen54 halamanLinear Regression and Correlation AnalysisMohit VermaBelum ada peringkat
- Linear Regression and Correlation Analysis PPT at BEC DOMSDokumen67 halamanLinear Regression and Correlation Analysis PPT at BEC DOMSBabasab Patil (Karrisatte)50% (2)
- Linear Regression (Simple & Multiple)Dokumen29 halamanLinear Regression (Simple & Multiple)O'Neil RobinsonBelum ada peringkat
- Measures of Association and Bivariate AnalysisDokumen66 halamanMeasures of Association and Bivariate Analysisramki66666Belum ada peringkat
- Simple Linear RegressionDokumen50 halamanSimple Linear RegressionRangothri Sreenivasa Subramanyam100% (1)
- Simple RegressionDokumen35 halamanSimple RegressionHimanshu JainBelum ada peringkat
- Regression Analysis Techniques and AssumptionsDokumen43 halamanRegression Analysis Techniques and AssumptionsAmer RahmahBelum ada peringkat
- Lec9 1Dokumen63 halamanLec9 1Kashef HodaBelum ada peringkat
- Chapter 16Dokumen6 halamanChapter 16maustroBelum ada peringkat
- ECONOMETRICSDokumen4 halamanECONOMETRICSAlix MuratetBelum ada peringkat
- Lecture 9: Linear Regression FundamentalsDokumen24 halamanLecture 9: Linear Regression FundamentalsAdila AnbreenBelum ada peringkat
- Linear RegressionDokumen56 halamanLinear RegressionOpus YenBelum ada peringkat
- Forecasting Cable Subscriber Numbers with Multiple RegressionDokumen100 halamanForecasting Cable Subscriber Numbers with Multiple RegressionNilton de SousaBelum ada peringkat
- Emet2007 NotesDokumen6 halamanEmet2007 NoteskowletBelum ada peringkat
- Chapter 2 SLRMDokumen40 halamanChapter 2 SLRMmerondemekets12347Belum ada peringkat
- Eco 2Dokumen31 halamanEco 2Nebiyu WoldesenbetBelum ada peringkat
- Ordinary Least SquaresDokumen21 halamanOrdinary Least SquaresRahulsinghooooBelum ada peringkat
- Regression Explains Variation in Dependent VariablesDokumen15 halamanRegression Explains Variation in Dependent VariablesJuliefil Pheng AlcantaraBelum ada peringkat
- Chapter 12: RegressionDokumen10 halamanChapter 12: RegressionAlok NegiBelum ada peringkat
- M. Amir Hossain PHD: Course No: Emba 502: Business Mathematics and StatisticsDokumen31 halamanM. Amir Hossain PHD: Course No: Emba 502: Business Mathematics and StatisticsSP VetBelum ada peringkat
- X X B X B X B y X X B X B N B Y: QMDS 202 Data Analysis and ModelingDokumen6 halamanX X B X B X B y X X B X B N B Y: QMDS 202 Data Analysis and ModelingFaithBelum ada peringkat
- Excel Regression Analysis ToolsDokumen19 halamanExcel Regression Analysis ToolsBiplove PokhrelBelum ada peringkat
- The Simple Linear Regression Model and CorrelationDokumen64 halamanThe Simple Linear Regression Model and CorrelationRajesh DwivediBelum ada peringkat
- Inference For RegressionDokumen24 halamanInference For RegressionJosh PotashBelum ada peringkat
- Topics: RegressionDokumen26 halamanTopics: RegressionramBelum ada peringkat
- Trip Generation AnalysisDokumen56 halamanTrip Generation AnalysisSourab VokkalkarBelum ada peringkat
- Estimating Demand FunctionDokumen45 halamanEstimating Demand FunctionManisha AdliBelum ada peringkat
- Linear Regression and Correlation: - 0 Positive Association - 0 Negative Association - 0 No AssociationDokumen31 halamanLinear Regression and Correlation: - 0 Positive Association - 0 Negative Association - 0 No AssociationSodhi NirdeepBelum ada peringkat
- Regression EquationDokumen56 halamanRegression EquationMuhammad TariqBelum ada peringkat
- Multiple Regression Analysis & ApplicationsDokumen23 halamanMultiple Regression Analysis & ApplicationsHarshul BansalBelum ada peringkat
- Regression and Multiple Regression AnalysisDokumen21 halamanRegression and Multiple Regression AnalysisRaghu NayakBelum ada peringkat
- Logistic RegressionDokumen37 halamanLogistic RegressionDhruv BansalBelum ada peringkat
- Statistics-Linear Regression and Correlation AnalysisDokumen50 halamanStatistics-Linear Regression and Correlation AnalysisDr Rushen SinghBelum ada peringkat
- Regression Analysis: Understanding the Key Concepts of Regression ModelsDokumen39 halamanRegression Analysis: Understanding the Key Concepts of Regression ModelsNavneet KumarBelum ada peringkat
- Simple LR LectureDokumen60 halamanSimple LR LectureEarl Kristof Li LiaoBelum ada peringkat
- Chapter 3 EconometricsDokumen34 halamanChapter 3 EconometricsAshenafi ZelekeBelum ada peringkat
- Basic Econometrics Revision - Econometric ModellingDokumen65 halamanBasic Econometrics Revision - Econometric ModellingTrevor ChimombeBelum ada peringkat
- Chapter 05 - MulticollinearityDokumen26 halamanChapter 05 - Multicollinearitymgayanan100% (1)
- 6.3 SSK5210 Parametric Statistical Testing - Analysis of Variance LR and Correlation - 2Dokumen39 halaman6.3 SSK5210 Parametric Statistical Testing - Analysis of Variance LR and Correlation - 2Sarveshwaran BalasundaramBelum ada peringkat
- Lecture+8+ +Linear+RegressionDokumen45 halamanLecture+8+ +Linear+RegressionSupaapt SrionBelum ada peringkat
- ECONOMETRICS BASICSDokumen89 halamanECONOMETRICS BASICSAnca AfloroaeiBelum ada peringkat
- Regression Basics: Predicting A DV With A Single IVDokumen20 halamanRegression Basics: Predicting A DV With A Single IVAmandeep_Saluj_9509Belum ada peringkat
- Chap 11Dokumen27 halamanChap 11Senelwa AnayaBelum ada peringkat
- Correlation and Regression AnalysisDokumen46 halamanCorrelation and Regression Analysisrienalen placaBelum ada peringkat
- 4 Regression IssuesDokumen44 halaman4 Regression IssuesarpitBelum ada peringkat
- RegressionDokumen24 halamanRegressionVaruni GuptaBelum ada peringkat
- Simple RegressionDokumen50 halamanSimple Regressioniga gemelia100% (1)
- Regression Analysis: Alok SrivastavaDokumen16 halamanRegression Analysis: Alok SrivastavagopiBelum ada peringkat
- Regression Formulas in Matrix FormDokumen6 halamanRegression Formulas in Matrix Formbhujakhia_748657110Belum ada peringkat
- Eco 3Dokumen68 halamanEco 3Nebiyu WoldesenbetBelum ada peringkat
- Week 9 ADokumen26 halamanWeek 9 AKarthi KeyanBelum ada peringkat
- The Delhi Metro ProjectDokumen13 halamanThe Delhi Metro ProjectVikas SainiBelum ada peringkat
- TelecomDokumen17 halamanTelecomVikas SainiBelum ada peringkat
- Classical MGMTDokumen30 halamanClassical MGMTnileshrollBelum ada peringkat
- BOP MarketingDokumen23 halamanBOP MarketingVikas SainiBelum ada peringkat
- SecuritasDokumen4 halamanSecuritasVikas SainiBelum ada peringkat
- Bottom of The Pyramid Marketing:: Dr. M S Balaji Assistant Professor IBS HyderabadDokumen23 halamanBottom of The Pyramid Marketing:: Dr. M S Balaji Assistant Professor IBS HyderabadVikas SainiBelum ada peringkat
- Green Product BRMDokumen17 halamanGreen Product BRMVikas SainiBelum ada peringkat
- Marketing EthicsDokumen42 halamanMarketing EthicsFazrul RosliBelum ada peringkat
- Affordable Housing - Ashish - JindalDokumen13 halamanAffordable Housing - Ashish - JindalJnanamBelum ada peringkat
- 7QCDokumen13 halaman7QCAniketh ShankarBelum ada peringkat
- 01 SL Veronese VSP InflationDokumen51 halaman01 SL Veronese VSP InflationVikas SainiBelum ada peringkat
- 01 SL Veronese VSP InflationDokumen51 halaman01 SL Veronese VSP InflationVikas SainiBelum ada peringkat
- Boilers: 27 Bureau of Energy EfficiencyDokumen28 halamanBoilers: 27 Bureau of Energy EfficiencyVikas Saini100% (1)
- Open Hole Logs Introduction GR SP CALDokumen21 halamanOpen Hole Logs Introduction GR SP CALmagedBelum ada peringkat
- Eee f111 Electrical Sciences1Dokumen3 halamanEee f111 Electrical Sciences1aryan mittalBelum ada peringkat
- Post GreeDokumen15 halamanPost GreeDwi PraptiBelum ada peringkat
- Biology Notes HSCDokumen107 halamanBiology Notes HSCGouri DasBelum ada peringkat
- A Conjunction Is The Glue That Holds WordsDokumen2 halamanA Conjunction Is The Glue That Holds WordsYamson MillerJrBelum ada peringkat
- Barrels & Actions by Harold HoffmanDokumen238 halamanBarrels & Actions by Harold HoffmanNorm71% (7)
- JefimenkoDokumen10 halamanJefimenkoBilly M. SpragueBelum ada peringkat
- Weld CheckDokumen6 halamanWeld CheckArnold c ElverBelum ada peringkat
- IP46 - Guide To Use BAPCO WPS & Welding ProceduresDokumen4 halamanIP46 - Guide To Use BAPCO WPS & Welding ProceduressajiBelum ada peringkat
- Virtual Retinal DisplayDokumen17 halamanVirtual Retinal Displaysaket_mnBelum ada peringkat
- Nov. AbwDokumen50 halamanNov. Abwjbyarkpawolo70Belum ada peringkat
- Earth and Life Science Test ReviewDokumen3 halamanEarth and Life Science Test Reviewmerlyn m romerov100% (1)
- Auditing The Usage of Therapeutic Footwear in Diabetic Foot Patients Through Amit Jain's Extended SCC' Classification For Therapeutic FootwearDokumen6 halamanAuditing The Usage of Therapeutic Footwear in Diabetic Foot Patients Through Amit Jain's Extended SCC' Classification For Therapeutic FootwearJosé MorenoBelum ada peringkat
- p-4500 Technical InformationDokumen13 halamanp-4500 Technical InformationElhoiBelum ada peringkat
- Ee242 Lect06 TwoportsDokumen32 halamanEe242 Lect06 TwoportsZyad IskandarBelum ada peringkat
- Daikin RXS-K - Technical DataDokumen21 halamanDaikin RXS-K - Technical DataPrestoneKBelum ada peringkat
- Richard A. Nyquist and Ronald O. Kagel (Auth.) - Handbook of Infrared and Raman Spectra of Inorganic Compounds and Organic Salts. Infrared Spectra of Inorganic Compounds-Academic Press (1971)Dokumen499 halamanRichard A. Nyquist and Ronald O. Kagel (Auth.) - Handbook of Infrared and Raman Spectra of Inorganic Compounds and Organic Salts. Infrared Spectra of Inorganic Compounds-Academic Press (1971)Patrícia Bodanese PratesBelum ada peringkat
- Network of Global Corporate Control. Swiss Federal Institute of Technology in ZurichDokumen36 halamanNetwork of Global Corporate Control. Swiss Federal Institute of Technology in Zurichvirtualminded100% (2)
- ME4111 Engineering and Mechanical PrinciplesDokumen5 halamanME4111 Engineering and Mechanical PrinciplesEdvard StarcevBelum ada peringkat
- DS White-Papers Getting Started With Business Logic 3DEXPERIENCE R2017x V1Dokumen52 halamanDS White-Papers Getting Started With Business Logic 3DEXPERIENCE R2017x V1AlexandreBelum ada peringkat
- QAP - LT Panel PDFDokumen8 halamanQAP - LT Panel PDFAkshay Ajay100% (2)
- (It Bus) Computer HistoryDokumen6 halaman(It Bus) Computer HistoryRica Elaine LubasanBelum ada peringkat
- Mic 2282Dokumen10 halamanMic 2282mariusz sBelum ada peringkat
- Connective TissueDokumen6 halamanConnective TissuecrtgyhujikBelum ada peringkat
- Gpa Calculation SheetDokumen1 halamanGpa Calculation SheetIryna HoncharukBelum ada peringkat
- Second Mid Term CE 461: Structural Analysis II: Student Name: Student No.: Section: 9 10 11 12Dokumen4 halamanSecond Mid Term CE 461: Structural Analysis II: Student Name: Student No.: Section: 9 10 11 12David Olorato NgwakoBelum ada peringkat
- Absorption QuestionsDokumen11 halamanAbsorption QuestionsRalph CastinoBelum ada peringkat
- DCT Dual Clutch TransmissionDokumen16 halamanDCT Dual Clutch TransmissionSudharshan SrinathBelum ada peringkat
- AdvancesDokumen328 halamanAdvanceshanumsj123Belum ada peringkat
- Ductile deformation finite strain analysisDokumen27 halamanDuctile deformation finite strain analysisJorgeBarriosMurielBelum ada peringkat