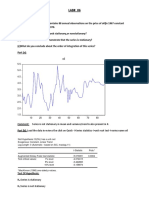
Test For Outliers

One of the important aim in the statistical tests is to

recognize the presene or absence of outliers
Outliers in a series of measurements are
extraordinarily small or large observations
compared with the bulk of the data
There are test procedures in order to detect outliers
in data and we will look at the Dixons Q-test
Q-test is one of the nost frequently used outlier test
procedure
Test For Outliers
The Q-test uses the range of measurements and
can be applied even when only few data are
available
The n measurements are arranged in ascending
order
If the very small value to be tested as an outlier is
denoted by x
1
and the very large value by x
n
Then the test statistic is calculated as given on the
next slide
Test For Outliers
For the smallest one
1
1 2
1
x x
x x
Q
n

=
Test For Outliers
For the Largest one
1
1
x x
x x
Q
n
n n
n

=

Test For Outliers
The null hypothesis, i.e, that the concidered
measurement is not an outlier, is accepted if the
quantity Q<Q(1-o;n).
If the calculated Q value is greather than the Table
value [Q>Q(1-a;n)], then we reject the null hypothesis and
say that the value is an outlier
Q values for selected significance and degrees of
freedom are given in table and in your book in
Table2.10
Example 2.8
Trace analysis of polycyclic aromatic hydrocarbons
(PAH) in a soil revealed for the trace constituent
benzo[a]pyrene the following values in mg/kg dry
weight

5.30, 5,00, 5.10, 5.20, 5.10, 6.20, 5.15
Apply the Q-test to check whether the smallest and
largest value might be an outlier
Example 2.8
First we need to arrange the data in an ascending
order as

5.00, 5,10, 5.10, 5.15, 5.20, 5.30, 6.20
The we can calculate the Q value for both smallest
and largest values as
083 . 0
00 . 5 20 . 6
00 . 5 10 . 5
1
1 2
1
=

=
x x
x x
Q
n
Example 2.8
For the largest value
75 . 0
00 . 5 20 . 6
30 . 5 20 . 6
1
1
=

=

x x
x x
Q
n
n n
n
For an o=0.01 we can use the table 2-10 and obtain the
table value as
Q(1-0.01=0.99;n=7)=0.64
Since the Q
1
value is much smaller (0.083) than the table
value we can not eliminate the smallest value as outlier
However, the Q
2
value is in fact larger than the table value
and for this reason we can eliminate the largest as outlier
F test Example
82 . 4 34 . 0
) 59 . 3 (
8 . 10
5 . 14
) 255 . 0 (
8 . 10
5 . 14
2
2
2
1
2
2
2
1
s s
s s
o
o
o
o
Confidence interval is
Grubbss Test for Outlier
) ; 1 (
*
n T
s
x x
T
table
o <

=
It can be applied for series of measurements consisting of 3 to
150 measuremets
The null hypothesis, according to which x* is not an outlier
within the measurement series of n values is accepted at level
o, if the test quantitity T is:




By use of the test quantity T, the distances of the suspicious
values from the mean are determined and related to the
standard deviation of the measurements
Grubbss Test for Outlier
21 . 2
411 . 0
20 . 6 29 . 5 *
71 . 0
411 . 0
00 . 5 29 . 5 *
1
=

=
=

=
s
x x
T
s
x x
T
n
Exmaple 2.9
The data for the trace analysis of benzo[a]pyrene from
previous example are also used in Grubbss test
The mean of the data was 5.29 and the standard deviation
was 0.411)
The we can calculate the T values for the smallest ans the
largest vales as
Grubbss Test for Outlier
21 . 2
411 . 0
20 . 6 29 . 5 *
71 . 0
411 . 0
00 . 5 29 . 5 *
1
=

=
=

=
s
x x
T
s
x x
T
n
Exmaple 2.9
The table value at an a=0.01 is
T(1-0.01=0.99;n=7) =2.10
As a result, the test results is not significant for the smallest
value but is significant for the largest value
So the largest one is an outlier
Non-parametric Tests for Method Comparison
The Tests that we have seen so far all requires that the data
must be normaly distributed.
In this case distribution free methods needs to be used
These methods do not require the parameters such as
mean and standard deviation used in the previous tests
For that reason, they are non-parametric methods
These methods require more replicate mesurements
The do not use the values of the quantitative variables
They use the rank of the data and are based on the
counting

Non-parametric Tests for Method Comparison
We will look at two example of non-parametric tests
These are:
The Mann-Whitney U-test for the comparison
of the independent samples
Wilcoxon T-test for for paqired measurements
When Normality isw doubtful, you should always
check these tests especially in the case of small
samples

The Mann-Whitney U-test
This test is based on the ranking the samples by taking the
both gruops (group A and group B ) of the data together
It gives the rank 1 to the lowest result and rank 2 to the
second ect.
If n1 and n2 are the number of data in the group with the
smallest and largest number of results, respectively, and R1
and R2 are the sum of the ranks in these two groups, then
we can we can set up the equations as:
( )
( )
2
2 2
2 1 2
1
1 1
2 1 1
2
1
2
1
R
n n
n n U
R
n n
n n U

+
+ =

+
+ =
The Mann-Whitney U-test
The smaller of the two U values is used to evaluate the test
When we have tie, the the average of the ranks are given.
The Mann-whitney test compares the median of the two
samples
The smaller the diffrerence between the medians, the
smaller the difference between U1and U2
( )
( )
2
2 2
2 1 2
1
1 1
2 1 1
2
1
2
1
R
n n
n n U
R
n n
n n U

+
+ =

+
+ =
2 1 1
2 1 0
:
:
U U H
U U H
=
=
The Mann-Whitney U-test
Example: The following two grops of
measuremets are to be compared
Here the lowest results, 10.8 is
given the rank 1.
Since we have 10.8 twice in group A
and B, they are both given the rank
of 1.5 as their average
A B
11.2 10.9
13.7 11.2
14.8 12.1
11.2 12.4
15.0 15.5
16.1 14.6
17.3 13.5
10.9 10.8
10.8
11.7
( )
5 . 1
2
2 1
=
+
= Rank
The Mann-Whitney U-test
If we set the
hypothesis as
This will be a two
sided test
Group result rank Group result rank
A 10.8 1.5 B 12.4 10
B 10.8 1.5 B 13.5 11
A 10.9 3.5 A 13.7 12
B 10.9 3.5 B 14.6 13
A 11.1 5 A 14.8 14
A 11.2 6.5 A 15.0 15
B 11.2 6.5 B 15.5 16
A 11.7 8 A 16.1 17
B 12.1 9 A 17.3 18
2 1 1
2 1 0
:
:
U U H
U U H
=
=
The Mann-Whitney U-test
R1 is the sum of the ranks in group B as:
R1=1.5+3.5+6.5+9+11+13+16=70.5
R2 is the sum of the ranks in group A as:
R2=1.5+3.5+6+6.5+8+10+12+14+15+17+18=100.5
( ) ( )
( ) ( )
5 . 34 ) , min(
that notice
5 . 34 5 . 100
2
1 10 10
10 * 8
2
1
5 . 45 5 . 70
2
1 8 * 8
10 * 8
2
1
2 1
2 1 2 1
2
2 2
2 1 2
1
1 1
2 1 1
= =
= +
=
+
+ =
+
+ =
=
+
+ =
+
+ =
U U U
n n U U
R
n n
n n U
R
n n
n n U
The Mann-Whitney U-test
From the table (Appendix, Table 4), for a two sided test with
n1=8 and n2=10, a value of 17 is found.
If an observed U value is les than or equal to the value in the
table, the null hypothesis may be rejected at the level of the
significance of the table.
Since our calculated value is larger than 17, we conclude
that no difference between the two groups.
( ) ( )
( ) ( )
5 . 34 ) , min(
that notice
5 . 34 5 . 100
2
1 10 10
10 * 8
2
1
5 . 45 5 . 70
2
1 8 * 8
10 * 8
2
1
2 1
2 1 2 1
2
2 2
2 1 2
1
1 1
2 1 1
= =
= +
=
+
+ =
+
+ =
=
+
+ =
+
+ =
U U U
n n U U
R
n n
n n U
R
n n
n n U
The Mann-Whitney U-test
We can now check the data used in this test have any
tendency to show normal distribution or not.
sample raw A raw B ranked ranked (j-0.5)/10 (j-0.5)/8 ranked (j-0.5)/18
1 11.20 10.90 10.80 10.80 0.05 0.06 10.80 0.03
2 13.70 11.20 10.90 10.90 0.15 0.19 10.80 0.08
3 14.80 12.10 11.20 11.20 0.25 0.31 10.90 0.14
4 11.20 12.40 11.20 12.10 0.35 0.44 10.90 0.19
5 15.00 15.50 11.70 12.40 0.45 0.56 11.20 0.25
6 16.10 14.60 13.70 13.50 0.55 0.69 11.20 0.31
7 17.30 13.50 14.80 14.60 0.65 0.81 11.20 0.36
8 10.90 10.80 15.00 15.50 0.75 0.94 11.70 0.42
9 10.80 16.10 0.85 12.10 0.47
10 11.70 17.30 0.95 12.40 0.53
11 13.50 0.58
12 13.70 0.64
13 14.60 0.69
14 14.80 0.75
15 15.00 0.81
16 15.50 0.86
17 16.10 0.92
18 17.30 0.97
The Mann-Whitney U-test
We can now check the data used in this test have any
tendency to show normal distribution or not.
Normal probabilty plot
0.00
0.25
0.50
0.75
1.00
10.00 12.00 14.00 16.00 18.00
Measurement
P
r
o
b
a
b
i
l
i
t
y
Group A
Group B
A and B
Wilcoxon Matched Pairs Signed-Rank test
In this test, difference of the (d
i
) paired data first calculated
These d
i
values are ranked first without regard to sign
starting with the smallest value.
Then the same sign is given as to corresponding difference
If there are ties, the same rule (take average) is applied as in
the Mann-Whitney test
If any di value is zero the you can either drop them from
analysis or assign a rank of (p+1)/2, in which p is the number
of zero differences
In this case half of the zero difference takes negative and
the other half positive rank
Wilcoxon Matched Pairs Signed-Rank test
The null hypohesis is that the methods A and B are equivalet
If Ho is true, it would be expected that that the sum of all
ranks for positive differences (T+) would be close to the sum
for negative differences (T-).
The test statistic is than for two sided case:

Wilcoxon T-test is calculated as: T= min (T+, T-)
The smaller the value of T, the larger the significance of the
difference

B A H
B A H
=
=
:
:
1
0
Wilcoxon Matched Pairs Signed-Rank test
Lets now do the example
sample R T d=R-T rank signed rank
1 114 116 -2 1 -1
2 49 42 7 7.5 7.5
3 100 95 5 4 4
4 20 10 10 9.5 9.5
5 90 94 -4 2.5 -2.5
6 106 100 6 5.5 5.5
7 100 96 4 2.5 2.5
8 95 102 -7 7.5 -7.5
9 160 150 10 9.5 9.5
10 110 104 6 5.5 5.5
Wilcoxon Matched Pairs Signed-Rank test
The critical (Table) value of T as a function of n and o are
given in Table 5 of appendix.
In our example, all positive differences adds up to T+=44.0
And all negative differences T-=11.0
If the calulated T value is equal to or smaller than the table
value, the null hyothesis is rejected.
For an o=0.05 and n=10 in our two sided test, the table
value is T=8.
Thus the nul hypothesis is accepted and we can conclude
that there is no diffrence between the two method