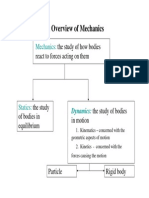
AOE 5104 Class 6

Online presentations for next class:

Equations of Motion 2
Homework 2
Homework 3 (revised this morning) due
9/18
dAlembert
Last class
Integral theorems
} }
= V
R S
dS d n | t |
} }
= V
R S
dS d n A A . . t
} }
= V
R S
dS d n A A t
} }
= V
C
S
S d s A n A d . .
and their limitations
2D flow over airfoil with O=0
C
V . V
= change in density in direction of V, multiplied by magnitude of V
Convective operator
Irrotational and
Solenoidal Fields
0 .
0
V V
V V
A
|
Class Exercise
1. Make up the most complex irrotational 3D velocity
field you can.
2 2 2 3 sin
/ 3 ) 2 cos ( z y x xy x e
x
k j i V + + = ?
We can generate an irrotational field by taking the gradient of any
scalar field, since
0 V V |
I got this one by randomly choosing
z y x e
x
/ 1
3 2 sin
+ + = |
And computing
k j i V
z y x c
c
+
c
c
+
c
c
=
| | |
Acceleration??
2
nd
Order Integral Theorems
Greens theorem (1
st
form)



Greens theorem (2
nd
form)
Volume R
with Surface S
dt
ndS
} }
c
c
= V V + V
S
R
S d d
n
2
|
t | |
} }
c
c
c
c
= V V
S
R
S d d
n
-
n
2 2

|
|
t | |
These are both re-expressions of the divergence theorem.
The Equations of Motion
Phrase of the Day
Mutationem motus proportionalem esse vi
motrici impressae, & fieri secundum lineam
rectam qua vis illa imprimitur.

Go Hokies?
Supersonic Turbulent Jet Flow and
Near Acoustic Field
Freund at al. (1997)
Stanford Univ.
DNS
Conservation Laws
Conservation of mass

Conservation of momentum

Conservation of energy


0 mass of C. O. R. =
Viscous Pressure Body
of C. O. R. F F F momentum + + =
Q W W W energy of C. O. R.
Viscous Pressure Body
+ + + =
Supersonic Turbulent Jet Flow and
Near Acoustic Field
Freund at al. (1997)
Stanford Univ.
DNS
Conservation Laws
Conservation of mass

Conservation of momentum

Conservation of energy


0 mass of C. O. R. =
Viscous Pressure Body
of C. O. R. F F F momentum + + =
Q W W W energy of C. O. R.
Viscous Pressure Body
+ + + =
Apply to the fluid material (not the space)
Experimental observations
Assumption: Fluid is a homogeneous continuum
flow


x
y
z
x y z = + + r i j k
o o o o
x y z = + + r i j k
1 o o, o
2 o o, o
3 o o, o
( , , )
( , , )
( , , )
x f x y z t
y f x y z t
z f x y z t
=
=
=
Position :
1) Lagrangian Method
Kinematics of Continua
1 o o, o
o o, o
2 o o, o 3 o o, o
( , , )
where partial derivative wrt time
holding ( , ) constant
( , , ) ( , , )
,
x
y z
Df x y z t
D
v
Dt Dt
x y z
Df x y z t Df x y z t
v v
Dt Dt
=
= =
Velocity :
DTM
2 2 2
1 o o, o 2 o o, o 3 o o, o
2 2 2
( , , ) ( , , ) ( , , )
, ,
Concept is straightforward, but difficult to implement, often would produce more
information than we need or want, and
x y z
D f x y z t D f x y z t D f x y z t
a a a
Dt Dt Dt
= = =
Acceleration :
doesn't fit the situation usually encountered
in fluid mechanics.
The Lagrangian Method is always used in solid mechanics :
DTM
P

o
x
( )
3 2
o o
3
6
P
y x lx
EI
=
( )
( )
3 2
o 1 o o o o o 2 o o o 3 o o o
( , , , ), 3 ( , , , ), 0 ( , , , )
6
P t
x x f x y z t y x lx f x y z t z f x y z t
EI
= = =
rad
D
Dt t
t
c
= +
c
c

`
c
)
Acceleration :
v v
a v v G
1) Lagrangian Method
1 o o, o
2 o o, o
3 o o, o
( , , )
( , , )
( , , )
x f x y z t
y f x y z t
z f x y z t
=

Position :
2) Eulerian Method
DTM
Position:
1 o o, o
2 o o, o
3 o o, o
( , , )

( , , )
( , , )
x
y
z
Df x y z t
v
Dt
Df x y z t
v
Dt
Df x y z t
v
Dt
=
=
=
Velocity :
( , , , )
( , , , )
( , , , )
x
y
z
v x y z t
v x y z t
v x y z t

Velocity :
solve for position
as a function of
time and name
express the velocity
as a function of time
and spatial position
denotes the derivative wrt time
holding the spatial position fixed,
often called the local derivative
WOW! big, big difference: velocity as
a function of time and spatial position,
not velocity as a function of time and
particle name

complication: laws governing motion
apply to particles (Lagrange), not to
positions in space
2
1 o o, o
2
2
2 o o, o
2
2
3 o o, o
2
( , , )

( , , )
( , , )
x
y
z
D f x y z t
a
Dt
D f x y z t
a
Dt
D f x y z t
a
Dt
=
=
=
Acceleration :
skip this step and do not try to find
the positions of fluid particles
Giuseppe Lodovico Lagrangia
(Joseph-Louis Lagrange)

born 25 January 1736 in Turin, Italy
died 10 April 1813 in Paris, France
Leonhard Paul Euler

born 15 April 1707 in Basel, Switzerland
died 18 September 1783 in St. Petersburg, Russia
DTM
Acceleration in the Eulerian Method:
x
y
z
r
dr
A fluid particle, represented as a blue dot in the figure,
moves from position to during the time interval .
Its velocity changes from ( , ) to ( , )
where be chosen
d dt
t d t dt
d dt
a
+
+ +
=

r r r
v r v r r
r MUST v
( , ) ( , ) D d t dt t
Dt dt
+ +
=
v v r r v r
( , ) ( , ) ( , ) ( , ) ( , ) ( , )
( , ) ( , )
= the derivative wrt time at a fixed location
( , ) ( , ) rad change in between two po
D d t dt t d t dt d t d t t
Dt dt dt
d t dt d t
dt t
d t t d
dt dt
+ + + + + + +
= =
+ + + c
c
+
= =
v v r r v r v r r v r r v r r v r
a
v r r v r r v
v r r v r v r v G ints in space at a fixed time
and are independent variables; so we are free to chose them anyway we want. In order
to follow a particle, we must chose : rad
dt
t d
d dt
t
c
= = +
c
r
v
r v a v v G
.
If at a given instant we draw a line with the property that every point on
the line passed through the same reference point at some earlier time, the result
is known as a streakline.

It is called a streakline because, if the particles are dyed as they pass through
the common reference point, the result will be a line of dyed particles (i.e., a
streak) through the flowfield.

If at a given instant the velocity is calculated at all points in the flowfield
and then a line is drawn with the property that the velocities of all of the particles
lying on that line are tangent to it, the result is known as a streamline.

Streamlines are the velocity field lines. They provide a snapshot of the flowfield,
a picture at an instant. The surface formed by all the streamlines that pass
through a closed curve in space forms a stream tube.
1 o o, o
2 o o, o
3 o o, o
( , , )
( , , )
( , , )
x f x y z t
y f x y z t
z f x y z t
=

These equations define a line in terms of the

parameter, , when are constant.
Such a line is called a pathline.
t
o o o
, , x y z
Perspectives
Eulerian Perspective the flow as as seen at fixed locations in space, or
over fixed volumes of space. (The perspective of most analysis.)

Lagrangian Perspective the flow as seen by the fluid material. (The
perspective of the laws of motion.)
Control volume: finite fixed
region of space (Eulerian)
Coordinate: fixed point in space
(Eulerian)
Fluid system: finite piece of the fluid material
(Lagrangian)
Fluid particle: differentially small finite piece
of the fluid material (Lagrangian)
III
II
I
flow
A system moving along in the flow occupies volumes
I and II at time t. During the next interval dt some of
the system moves out of II into three and some
moves out of I into II. The rate of change of an
arbitrary property of the system, N, is given by the
following:
The Transport Theorem:
( ) ( ) ( ) ( ) ( ) ( ) in II & III at in I & II at in II at in II at in III at in I at

II II
N t dt N t N t dt N t N t dt N t DN
Dt dt dt dt
dV dS
t
q q
+ + +
= = +
c
= +
c
}}} }}
v n
the unit vector
normal
to ABC, n
two triangular elements from the
family approximating the surface of
volume II at time = t
the same two material elements,
but now approximating the
surface of volume III at time =
material that flowed through the
surface of volume II during the
interval and now fills volume III:

S A
dt v
( ) dN dt S q A = v n
DTM
A
B
C
C
A
B
Strategy
Write down equations of motion for
Lagrangian rates of change seen by fluid
particle or system
Derive relationship between Lagrangian
and Eulerian rates of change
Substitute to get Eulerian equations of
motion
Conservation of Mass
From a Lagrangian Perspective
Law: Rate of Change of Mass of Fluid Material = 0
For a Fluid Particle:
Volume dt
Density
0 .
0 .
0
1
0
0
= + V
=
c
c
+ V
=
c
c
+
c
c
=
c
c
+
c
c
=
c
c
Dt
D
t
t t
d
d
t
d
t
d
t
d
part
part part
part part
part

t
t

t
t

t
V
V
For a Fluid System:
dt
Volume R
Density
=(x,y,z,t)
where
part
t Dt
D
c
c

is referred to as
the SUBSTANTIAL DERIVATIVE
(or total, or material, or Lagrangian)
Seen by the
particle
0
0
=
=
c
c
}
}
R
R sys
d
Dt
D
d
t
t
t
AXIOMATA SIVE LEGES MOTUS
Lex I.
Corpus omne perseverare in statuo suo quiescendi vel movendi
uniformiter in directum, nisi quatenus a viribus impressis cogitur
statum illum mutare.
Lex II.
Mutationem motus proportionalem esse vi motrici impressae, &
fieri secundum lineam rectam qua vis illa imprimitur.
Lex III.
Actioni contrariam semper & qualem esse reactionem: sive
corporum duorum actiones in se mutuo semper esse quales &
in partes contrarias dirigi.
Corol. I.
Corpus viribus conjunctis diagonalem parallelogrammi eodem
tempore describere, quo latera separatis.

Conservation of Momentum
From a Lagrangian Perspective (Fluid Particle)
Law: Rate of Change of Momentum = F
body
+F
pressure
+F
viscous

Dt
D
d
t
d
t
d
part part
V V V
t t
t
=
c
c
=
c
c
= ROC of Momentum
F
body
: t d f =
dy
dx
dz
j
i
k
P
Net
density
volume dt
velocity V
body force per unit mass f
2
dy
y
yy
yy
c
c

t
t
2
dz
z
zy
zy
c
c

t
t
2
dy
y
p
p
c
c

Elemental Volume, Surface Forces

x, i
y, j
z, k
2
dy
y
p
p
c
c
+
Sides of volume have lengths dx, dy, dz
2
dy
y
yy
yy
c
c
+
t
t
2
dz
z
zy
zy
c
c
+
t
t
Volume dt = dxdydz
Density
Velocity V
2
2
dx
y
dx
y
xy
xy
xy
xy
c
c

c
c
+
t
t
t
t
On front
and rear
faces
y-component
Conservation of Momentum
From a Lagrangian Perspective (Fluid Particle)
Law: Rate of Change of Momentum = F
body
+F
pressure
+F
viscous

Dt
D
d
t
d
t
d
part part
V V V
t t
t
=
c
c
=
c
c
= ROC of Momentum
F
body
:
F
pressure
:
t d f =
t
t
d p so
d
y
p
dxdz dy
y
p
p dxdz dy
y
p
p component y
pressure
V =
c
c
=
|
|
.
|

\
|
c
c
+
|
|
.
|

\
|
c
c
=
F
j j j
2
1
2
1
dy
dx
dz
j
i
k
P
2
dy
y
p
p
c
c

P
x, i
y, j
z, k
2
dy
y
p
p
c
c
+
Conservation of Momentum
From a Lagrangian Perspective (Fluid Particle)
Law: Rate of Change of Momentum = F
body
+F
pressure
+F
viscous

Dt
D
d
t
d
t
d
part part
V V V
t t
t
=
c
c
=
c
c
= ROC of Momentum
F
body
:
F
pressure
:
F
viscous
:
t d f =
t
t
d p so
d
y
p
dxdz dy
y
p
p dxdz dy
y
p
p component y
pressure
V =
c
c
=
|
|
.
|

\
|
c
c
+
|
|
.
|

\
|
c
c
=
F
j j j
2
1
2
1
t
t t t t
t
t
t
t
t
t
t
t
t
t
t
d
z y x
dxdy dz
z
dxdy dz
z
dydz dx
x
dydz dx
x
dxdz dy
y
dxdz dy
y
component y
zy yy xy zy
zy
zy
zy
xy
xy
xy
xy
yy
yy
yy
yy
j j j
j j
j j
|
|
.
|

\
|
c
c
+
c
c
+
c
c
=
|
|
.
|

\
|
c
c

|
|
.
|

\
|
c
c
+
+
|
|
.
|

\
|
c
c

|
|
.
|

\
|
c
c
+
+
|
|
.
|

\
|
c
c

|
|
.
|

\
|
c
c
+
2
1
2
1
2
1
2
1
2
1
2
1
...
Likewise for
x and z
dy
dx
dz
j
i
k
P
2
dz
z
zy
zy
c
c

t
t
P
x, i
y, j
z, k
2
dy
y
yy
yy
c
c
+
t
t
2
dz
z
zy
zy
c
c
+
t
t
2
dy
y
yy
yy
c
c

t
t
Conservation of Momentum
From a Lagrangian Perspective (Fluid Particle)
Law: Rate of Change of Momentum = F
body
+F
pressure
+F
viscous

Dt
D
d
t
d
t
d
part part
V V V
t t
t
=
c
c
=
c
c
= ROC of Momentum
F
body
:
F
pressure
:
F
viscous
:
t d f =
t
t
d p so
d
y
p
dxdz dy
y
p
p dxdz dy
y
p
p component y
pressure
V =
c
c
=
|
|
.
|

\
|
c
c
+
|
|
.
|

\
|
c
c
=
F
j j j
2
1
2
1
t
t t t t
t
t
t
t
t
t
t
t
t
t
t
d
z y x
dxdy dz
z
dxdy dz
z
dydz dx
x
dydz dx
x
dxdz dy
y
dxdz dy
y
component y
zy yy xy zy
zy
zy
zy
xy
xy
xy
xy
yy
yy
yy
yy
j j j
j j
j j
|
|
.
|

\
|
c
c
+
c
c
+
c
c
=
|
|
.
|

\
|
c
c

|
|
.
|

\
|
c
c
+
+
|
|
.
|

\
|
c
c

|
|
.
|

\
|
c
c
+
+
|
|
.
|

\
|
c
c

|
|
.
|

\
|
c
c
+
2
1
2
1
2
1
2
1
2
1
2
1
...
k j i f
V
) . ( ) . ( ) . (
z y x
p
Dt
D
V + V + V + V =
So,
k j i
k j i
k j i
zz yz xz z
zy yy xy y
zx yx xx x
t t t
t t t
t t t
+ + =
+ + =
+ + =
where
Likewise for
x and z
dy
dx
dz
j
i
k
P
AXIOMS CONCERNING MOTION
Law 1.
Every body continues in its state of rest or of uniform motion in a
straight line, unless it is compelled to change that state by forces
impressed upon it.
Law 2.
Change of motion is proportional to the motive force impressed;
and is in the same direction as the line of the impressed force.
Law 3.
For every action there is always an opposed equal reaction; or,
the mutual actions of two bodies on each other are always equal
and directed to opposite parts.
Corollary 1.
A body, acted on by two forces simultaneously, will describe the
diagonal of a parallelogram in the same time as it would describe
the sides by those forces separately.

Isaac Newton
1642-1727
Conservation of Energy
From a Lagrangian Perspective (Fluid Particle)
Law: Rate of Change of Energy = W
body
+W
pressure
+W
viscous
+Q

Total energy is internal energy + kinetic energy
= e + V
2
/2 per unit mass
Rate of work (power) = force x velocity in
direction of force
Fouriers law to gives rate of heat added by
conduction

Dt
V e D
d
t
V e d
part
) ( ) (
2
2
1
2
2
1
+
=
c
+ c
= t
t
ROC of Energy
W
body

t d V f. =
dy
dx
dz
j
i
k
P
2
dy
y
v
v
c
c

2
dy
y
p
p
c
c

Elemental Volume, Surface Force

Work and Heat Transfer
x, i
y, j
z, k
2
dy
y
p
p
c
c
+
Sides of volume have lengths dx, dy, dz
Volume dt = dxdydz
Density
Velocity V
y-contributions
2
dy
y
v
v
c
c
+
Viscous work
requires expansion
of v velocity on all
six sides
2
dy
y
y
T
k
y
T
k
c
|
.
|

\
|
c
c
c

c
c

Velocity
components
u, v, w
2
dy
y
y
T
k
y
T
k
c
|
.
|

\
|
c
c
c
+
c
c
Conservation of Energy
From a Lagrangian Perspective (Fluid Particle)
Law: Rate of Change of Energy = W
body
+W
pressure
+W
viscous
+Q

Dt
V e D
d
t
V e d
part
) ( ) (
2
2
1
2
2
1
+
=
c
+ c
= t
t
ROC of Energy
W
body

W
pressure

W
viscous

t d V f. =
t d p ) .( V V =
t d w v u
z y x
) ) .( ) .( ) .( ( V + V + V =
Q:
t
t
d T k Q so
d
y
T
k
y
dxdz dy
y
T
k
y y
T
k dxdz dy
y
T
k
y y
T
k on contributi y
) .(
2
1
2
1
V V =
|
|
.
|

\
|
c
c
c
c
=
|
|
.
|

\
|
|
|
.
|

\
|
c
c
c
c

c
c

|
|
.
|

\
|
|
|
.
|

\
|
c
c
c
c
+
c
c
=
) .( ) .( ) .( ) .( ) .( .
) (
2
2
1
T k w v u p
Dt
V e D
z y x
V V + V + V + V + V =
+
V V f
So,
Equations for Changes Seen From
a Lagrangian Perspective
0 = d
Dt
D
R
t
}
} } } }
S
z y x
S R R
dS ) . ( + ) . ( + ) . ( + dS p - d = d
Dt
D
k n j n i n n f V t t
| | dS T). k( + dS . + + p - + d . = d )
2
V
+ (e
Dt
D
S S
z y x
R
2
R
} } } }
V + n V k n j n i n n f V ) . ( ) . ( ) . ( t t
Differential Form (for a particle)
Integral Form (for a system)
V . V =

Dt
D
k j i f
V
) . ( ) . ( ) . (
z y x
p
Dt
D
V + V + V + V =
) .( ) .( ) .( ) .( ) .( .
) (
2
2
1
T k w v u p
Dt
V e D
z y x
V V + V + V + V + V =
+
V V f
Conversion from Lagrangian to
Eulerian rate of change - Derivative
x
y
z
o(x(t),y(t),z(t),t)
o
o
o o o o o o o o
o o
V +
c
c
=
c
c
+
c
c
+
c
c
+
c
c
=
c
c
c
c
+
c
c
c
c
+
c
c
c
c
+
c
c
=

c
c
. V
t
z
w
y
v
x
u
t t
z
z t
y
y t
x
x t
Dt
D
t
part
The Substantial Derivative
Time Derivative Convective Derivative
Conversion from Lagrangian to
Eulerian rate of change - Integral
x
y
z
The Reynolds
Transport
Theorem
} }
}
}
}
}
} } }
+
c
c
=
|
.
|

\
|
V +
c
c
=
|
.
|

\
|
V + V +
c
c
=
V + =
+ =
=
c
c
S R
R
R
R
R
R R R sys
dS d
t

d
t

d
t

d d
Dt
D
Dt
Dd
d
Dt
D

Dt
d D
d
Dt
D
= d
t
n V
V
V V
V
.
) .(
. .
.
o t
t o
o
t o o
o
t o t
o
t
o t
o
t o
t o t o
o
o o
V +
c
c
= . V
t Dt
D
Volume R
Surface S
Apply
Divergence
Theorem
Equations for Changes Seen From
a Lagrangian Perspective
0 = d
Dt
D
R
t
}
} } } }
S
z y x
S R R
dS ) . ( + ) . ( + ) . ( + dS p - d = d
Dt
D
k n j n i n n f V t t
| | dS T). k( + dS . + + p - + d . = d )
2
V
+ (e
Dt
D
S S
z y x
R
2
R
} } } }
V + n V k n j n i n n f V ) . ( ) . ( ) . ( t t
Differential Form (for a particle)
Integral Form (for a system)
V . V =

Dt
D
k j i f
V
) . ( ) . ( ) . (
z y x
p
Dt
D
V + V + V + V =
) .( ) .( ) .( ) .( ) .( .
) (
2
2
1
T k w v u p
Dt
V e D
z y x
V V + V + V + V + V =
+
V V f
part
t Dt
D
c
c
=
Equations for Changes Seen From
an Eulerian Perspective
Differential Form (for a fixed volume element)
Integral Form (for a system)
0 = dS d
t
S R
} }
+
c
c
n V. t

} } } } }
+
c
c
S
z y x
S R R
dS ) . ( + ) . ( + ) . ( + dS p - d = dS d
t
k n j n i n n f n V V
V
t t

) . (
| | dS T). k( + dS . + + p - + d . = dS
V
+ e d )
t
V
+ e
S S
z y x
R S
2
2
R
} } } } }
V + +
c
c
n V k n j n i n n f V n V ) . ( ) . ( ) . ( . ) (
) (
2
1 2
1
t t

V . V =

Dt
D
k j i f
V
) . ( ) . ( ) . (
z y x
p
Dt
D
V + V + V + V =
) .( ) .( ) .( ) .( ) .( .
) (
2
2
1
T k w v u p
Dt
V e D
z y x
V V + V + V + V + V =
+
V V f
V +
c
c
= . V
t Dt
D
Equivalence of Integral and
Differential Forms
0 = dS d
t
S R
} }
+
c
c
n V. t

( ) t d = dS
R
S
} }
V V n V . .
( ) 0 . =
|
.
|

\
|
V +
c
c
}
t

d
t
R
V
( ) 0 . = V +
c
c
V

t
0 . . = V + V +
c
c
V V

t
V . V =

Dt
D
Cons. of mass
(Integral form)
Divergence
Theorem
Conservation of
mass for any
volume R
Then we get or
Cons. of mass
(Differential form)