What kind of coat can be put on only when

wet?

A coat of paint.
u
u
u
cos
sin
tan =
1 cos sin
2 2
= + u u
u
u
sin
1
csc =
Identity:
A mathematical statement that
is true for all values of the
given variables. In other words,
its an equation that is true no
matter what angle is
substituted into it.
Note: if the identity involves fractions, the
denominators cannot be zero. Any restrictions on a
variable must be stated.
Good News! Youre already familiar with some
trig identities!
sin
y
r
u = cos
x
r
u = tan
y
x
u =
2 2 2
where x y r + =
Basic I dentities
Reciprocal I dentities
u
u
sin
1
csc =
u
u
cos
1
sec =
u
u
tan
1
cot =
where sin , cos , and tan 0
We can use the basic
and reciprocal
identities to help prove
other identities!
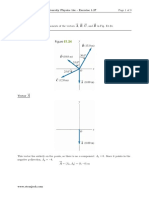
Prove the following quotient identity for all angles,
, where 0 360:

u
u
u
cos
sin
tan =
Step 1:
Set L.S. = R.S.
LS RS
u tan
u
u
cos
sin
=
x
y
Step 2:
Since can be
greater than 90,
re-write tan , sin ,
and cos in terms of
x, y, and r
|
.
|

\
|
|
.
|

\
|
=
r
x
r
y
Step 3:
Simplify each side,
where possible
x
y
x
r
r
y
=
1
1
Step 4:
Write conclusion
x
y
x
y
=
L.S. = R.S. Therefore, for all
angles 0 360 and 90or 270
u
u
u
cos
sin
tan =
We can use identities to derive other identities. When
proving an identity we must:

treat the left side (L.S.) and the right side (R.S.) separately

work until both sides represent the same expression
Proving Identities
Prove the following Pythagorean identity for all
angles, , where 0 360:



1 cos sin
2 2
= + u u
LS RS
u u
2 2
cos sin +
1 =
u u u u cos cos sin sin +
=
Therefore,
for all angles, , where 0
360
1 cos sin
2 2
= + u u
When proving trigonometric
identities, sometimes it will be
helpful for some part of your
equation (either one side or
both sides) to have a common
denominator (to simplify).
Lets try an example using a common denominator
Prove the following Pythagorean identity for all
angles, , between 0 and 360 except 0, 180, and
360



| |
2 2
csc cot 1 = +
Always express reciprocal
trig ratios in terms of
primary ratios (sine, cosine,
and tangent)
LS RS
|
2
csc
=
|
2
cot 1+
Therefore,
for all angles, , where 0 360
| |
2 2
csc cot 1 = +
When proving trigonometric
identities, sometimes it will be
helpful for you to simplify by
factoring your expression,
then cancelling any common
factors in the numerator and
denominator
Lets try an example using factoring
Prove the following identity for all angles, x,
between 0 and 360, where cos x 0:



) sin 1 )( (cos
sin sin
tan
2
x x
x x
x
+
+
=
LS RS
x tan
) sin 1 )( (cos
sin sin
2
x x
x x
+
+
=
) sin 1 )( (cos
) sin 1 ( sin
x x
x x
+
+
=
Therefore

for all angles, x, between 0 and 360, where cos x 0
) sin 1 )( (cos
sin sin
tan
2
x x
x x
x
+
+
=
Identities
Based on
Definitions
Identities Derived from
Relationships
Reciprocal Identities Quotient Identities Pythagorean Identities
u
u
sin
1
csc =
where
sin 0
u
u
cos
1
sec =
where
cos 0
u
u
tan
1
cot =
where
tan 0
u
u
u
cos
sin
tan =
where
cos 0
u
u
u
sin
cos
cot =
where
sin 0
1 cos sin
2 2
= + u u
u u
2 2
sec tan 1 = +
u u
2 2
csc cot 1 = +
To prove that a given trigonometric equation is an
identity, both sides of the equation need to be
shown to be equivalent. We can do this by:
Simplifying the more complicated side until it is
identical to the other side (or manipulate both sides to
get the same expression)
Rewriting all trig ratios in terms of x, y, and r
Rewriting all expressions involving tangent and the
reciprocal trig ratios in terms of sine and cosine
Applying the Pythagorean identity where appropriate
Using a common denominator or factoring as required