MATERI - 7 Kehilangan Energi
Diunggah oleh
Sandro Nainggolan BrabDeskripsi Asli:
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
MATERI - 7 Kehilangan Energi
Diunggah oleh
Sandro Nainggolan BrabHak Cipta:
Format Tersedia
1
HYDRAULICS
HEAD (ENERGY) LOSSES
PIPE FLOW
SECTION 7
2
INTRODUCTION
1. A pipe is a closed conduit which is used for carrying fluids under
pressure.
2. Pipes are commonly circular in sections.
3. As the pipes carry fluids under pressure, the pipe always run full.
4. The fluid flowing in the pipe is always subjected to resistence due
o shear forces between fluid particles and the boundary walls of
the pipe and between the fluid particles themselves resulting
from the viscosity of the fluid.
5. A certain amount of energy possesessed by the flowing fluid will
be consumed in overcoming this resistence to the flow, there will
always be some loss of energy in the direction of flow.
3
TYPE OF FLOW IN PIPE (1/2)
There are two types of flow in the pipe:
Laminar flow, and
Turbulent flow.
Based on the Osborne Reynold experiment (1883), the
occurrence of a laminar and turbulent flow as governed
by the relative magnitudes od the inertia and the viscous
force.
u
F
F
Force Viscous
Force Inertia
R
t
e
= =
VL
R
e
=
Re = Reynold number
V = Characteristic (representative)
velocity
L = Characteristic linear dimension
= mass density of fluid
= viscosity of flowing fluid, and
= kinematic viscosity (/)
4
Based on the Reynold experiment, he dedided
that:
Laminar flow occured when the Reynolds number
less then 2.000, all turbulence entering the flow
can be damped out by viscosity
Turbulent flow occurred when Reynolds number
greater then 4.000.
When the Reynolds numbers between 2.000 and
4.000, the flow is in transition condition.
TYPE OF FLOW IN PIPE (2/2)
5
CONTINUITY EQUATION
Consider to small section of flow in the tube, the mass flow
entering the tube per second is equal to that flowing out
from the tube per second, as there is no mass flow
crossing the tube, then :
v
2
,
2
v
1
,
1
A
1
A
2
dA
1
dA
2
2 2 2 1 1 1
dA V dA V =
V
1
and V
2
= mean flow velocity at section
1 and 2, respectively
dA
1
andA
2
= cross section area of the tube
1
and
2
= mass density
Continuity equation: A
1
V
1
= A
2
V
2
= Q
6
BERNOULLI EQUATION
Bernoulli equation:
tan kons
g 2
V
g
p
z
2
= +
+
g
p
g 2
V
2
Where:
Z : elevation head
: pressure head
: velocity head
g 2
V
g
p
z
g 2
V
g
p
z
2
2 2
2
2
1 1
1
+
+ = +
+
Energy equation along the pipe:
For a real fluid, energy losses should be considered, so:
f
2
2 2
2
2
1 1
1
h
g 2
V
g
p
z
g 2
V
g
p
z + +
+ = +
+
7
LAWS OF FLUID FRICTION
The frictional resistance offered to the low depends on type of flow.
The frictional resistance in the laminar flow is:
1. Propostional to the velocity of flow
2. Independent of the pressure
3. Proportional to the area of surface in contact
4. Independent of the nature of the surface in contact
5. Greately affected by variation of the temperature of the flowing fluid
The frictional resistance of the turbulent flow is:
1. Proportional to (velocity)
n
, n = 1.7 to 2.0
2. Independent of pressure
3. Slighly affected by variation of the temperature of the flowing fluid
4. Proportional to the area of surface in contact
5. Dependent on the nature of the surface in contact
8
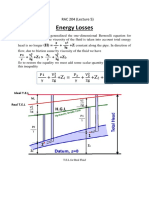
HEAD (ENERGY) LOSSES
1. The head or energy losses in flow in a pipe are made up of
friction losses (major losses) and local losses (minor losses)
2. Major losses are caused by forces between the liquid and the
solid boundary (distributed along the length of the pipe)
3. Minor losses are caused by disruptions to the flow at local
features like bends and changes in cross section
4. The distribution of losses, and other components can be shown
by two imaginary lines:
1) The energy grade line (EGL) is drawn a vertical distance
from the datum equal to the total head
2) The hydraulic grade line (HGL) is drawn a vertical distance
below the energy grade line equal to the velocity head
9
MAJOR LOSSES
f
2
2 2
2
2
1 1
1
h
g 2
V
g
p
z
g 2
V
g
p
z + +
+ = +
+
Based on the Bernoulli equation:
2 1
2 1
f
Z Z
g
p p
h +
=
Untuk pipa seragam, v
1
= v
2
Sehingga:
A . g
PL
hf
0
t
=
f 0
f
0
gRS
L
h
gR
= t
= t
gD 2
LV
h
2
f
=
is nondimensional constante
Darcy-Weisbach:
g 2
v
2
1
g 2
v
2
2
h
f
g
p
1
g
p
2
z
1
z
2
S
f
L
HGL
EGL
10
MINOR LOSSES
1. Loss of energy due to sudden enlargement:
2. Loss of energy due to sudden contraction:
3. Loss of energy at the entrance to a pipe:
4. Loss of energy at the exit from a pipe:
5. Loss of energy due to gradual contraction
or enlargement:
7. Loss of energy in the bends:
8. Loss of energy in various pipe fitting:
g 2
V
5 . 0 h
2
L
=
( )
g 2
V V
h
2
2 1
L
=
g 2
V
5 . 0 h
2
L
=
g 2
V
h
2
L
=
g 2
V
k h
2
L
=
( )
g 2
V V
k h
2
2 1
L
=
g 2
V
k h
2
L
=
11
Anda mungkin juga menyukai
- Modern Electrical Installation for Craft StudentsDari EverandModern Electrical Installation for Craft StudentsPenilaian: 4.5 dari 5 bintang4.5/5 (4)
- Hydraulics Open Channel FlowDokumen63 halamanHydraulics Open Channel FlowAchal I100% (2)
- Electronic Devices and Circuits: The Commonwealth and International Library: Electrical Engineering Division, Volume 1Dari EverandElectronic Devices and Circuits: The Commonwealth and International Library: Electrical Engineering Division, Volume 1Belum ada peringkat
- 8.2 - Aerodynamics PDFDokumen43 halaman8.2 - Aerodynamics PDFjeremy_scerri100% (1)
- Detailed Open Channel HydraulicsDokumen404 halamanDetailed Open Channel Hydraulicspcguru.oregon5759100% (3)
- Friction Losses in A Series of PipesDokumen19 halamanFriction Losses in A Series of PipesJohn Paul CordovaBelum ada peringkat
- Polymer Flooding IntroductionDokumen50 halamanPolymer Flooding IntroductionAlexandra Cuellar GuasdeBelum ada peringkat
- Expt 1 - Friction Loses in PipesDokumen20 halamanExpt 1 - Friction Loses in PipesFauzi Helmi67% (6)
- Electronic Devices and Circuits: In Three VolumesDari EverandElectronic Devices and Circuits: In Three VolumesPenilaian: 3.5 dari 5 bintang3.5/5 (2)
- Transport Phenomena I EssentialsDari EverandTransport Phenomena I EssentialsPenilaian: 2.5 dari 5 bintang2.5/5 (3)
- Experiment On Friction in PipesDokumen15 halamanExperiment On Friction in PipesVijay ShetBelum ada peringkat
- Steady Conduit FlowDokumen13 halamanSteady Conduit FlowEyuelAdamBelum ada peringkat
- History MatchDokumen78 halamanHistory MatchGustaf100% (2)
- Computational HydraulicsDokumen404 halamanComputational HydraulicsAbhishek Master100% (1)
- Experiment 1 - Friction Losses in Pipes-ReportDokumen41 halamanExperiment 1 - Friction Losses in Pipes-ReportKhairil Ikram67% (3)
- Experiment 1 - Friction Losses in Pipes-ReportDokumen41 halamanExperiment 1 - Friction Losses in Pipes-ReportKhairil Ikram68% (53)
- Codes For Lubricants Acc. DIN 51502Dokumen5 halamanCodes For Lubricants Acc. DIN 51502Anonymous alQXB11EgQ80% (10)
- Fluid 08Dokumen159 halamanFluid 08Marco MeraBelum ada peringkat
- Chapter 4Dokumen106 halamanChapter 4lockas222Belum ada peringkat
- EN-FAB Custody Transfer (LACT) & Meter ProversDokumen28 halamanEN-FAB Custody Transfer (LACT) & Meter Proverscarmel BarrettBelum ada peringkat
- Reverse Osmosis SystemsDokumen38 halamanReverse Osmosis SystemsChevronelle100% (1)
- Feynman Lectures Simplified 2C: Electromagnetism: in Relativity & in Dense MatterDari EverandFeynman Lectures Simplified 2C: Electromagnetism: in Relativity & in Dense MatterBelum ada peringkat
- E4 Lab Sheet Minor Losses in PipeDokumen17 halamanE4 Lab Sheet Minor Losses in PipeHoongBelum ada peringkat
- Fluid Mechanics and Pressure DropDokumen48 halamanFluid Mechanics and Pressure DroppraSHANT2331Belum ada peringkat
- SKCK Donri EditDokumen1 halamanSKCK Donri EditSandro Nainggolan BrabBelum ada peringkat
- Contoh Soal Metode CROSSDokumen15 halamanContoh Soal Metode CROSSSalamun Hafiz89% (9)
- Hydrocyclone SeparatorDokumen2 halamanHydrocyclone Separatorgautam_96948069100% (1)
- AutoCAD 2015 Keygen XDokumen5 halamanAutoCAD 2015 Keygen XSandro Nainggolan BrabBelum ada peringkat
- Pressure Test, Flushing & Air Blowing Procedure For PipingDokumen17 halamanPressure Test, Flushing & Air Blowing Procedure For Pipingsoumaya yahyaoui100% (8)
- Fluids U IIIDokumen11 halamanFluids U IIIR Raj Singh SinghBelum ada peringkat
- Fluid Friction in Pipes and Losses From Fittings: ObjectivesDokumen4 halamanFluid Friction in Pipes and Losses From Fittings: ObjectivesOsamaBelum ada peringkat
- EAT259 Chapter 1 IntroductionDokumen34 halamanEAT259 Chapter 1 IntroductionAbdullahi Dirie AbdiBelum ada peringkat
- Kehilangan Dalam PaipDokumen5 halamanKehilangan Dalam PaipArmalina NacaBelum ada peringkat
- 48 - 25795 - ME362 - 2020 - 1 - 2 - 1 - Lecture 11 - Fluid 1 - Flow Through Pipes - Part IDokumen20 halaman48 - 25795 - ME362 - 2020 - 1 - 2 - 1 - Lecture 11 - Fluid 1 - Flow Through Pipes - Part IHussien El-masryBelum ada peringkat
- Experiment 1 - Friction Losses in PipesDokumen34 halamanExperiment 1 - Friction Losses in PipesKhairil Ikram33% (3)
- Persamaan Energi Dalam Aliran InternalDokumen28 halamanPersamaan Energi Dalam Aliran InternalLativa Putry AFiznaBelum ada peringkat
- Pipe Flow Notes - BasicDokumen9 halamanPipe Flow Notes - BasicMwine Isaac NormanBelum ada peringkat
- 48 - 25795 - ME362 - 2020 - 1 - 2 - 1 - Lecture 7 - Fluid 1 - Flow MeasurementsDokumen19 halaman48 - 25795 - ME362 - 2020 - 1 - 2 - 1 - Lecture 7 - Fluid 1 - Flow Measurementssishu21Belum ada peringkat
- Flow Through PipesDokumen6 halamanFlow Through PipesammuvijjiBelum ada peringkat
- Pipe Flow - Upadhyay 2017Dokumen35 halamanPipe Flow - Upadhyay 2017John Ceasar PascoBelum ada peringkat
- Lec. 8 Pipes PDFDokumen40 halamanLec. 8 Pipes PDFسامر فؤاد الشخريتBelum ada peringkat
- Pipe Flow: Major and Minor Losses: Puja Upadhyay Florida Center For Advanced Aero - PropulsionDokumen35 halamanPipe Flow: Major and Minor Losses: Puja Upadhyay Florida Center For Advanced Aero - PropulsionJohn Ceasar PascoBelum ada peringkat
- 1.2 Review of Hydraulic FluidsDokumen31 halaman1.2 Review of Hydraulic FluidsHailemariam WeldegebralBelum ada peringkat
- Thermo Fluids - ME 439: Arab Academy For Science, Technology and Maritime TransportationDokumen24 halamanThermo Fluids - ME 439: Arab Academy For Science, Technology and Maritime TransportationFrank Masing FrancisBelum ada peringkat
- Shell Momentum BalancesDokumen48 halamanShell Momentum BalancesJuan CarvajalBelum ada peringkat
- Flow Through Pipes: Fluid MechanicsDokumen20 halamanFlow Through Pipes: Fluid MechanicsSantosh TrimbakeBelum ada peringkat
- FM Minor Losses 1Dokumen14 halamanFM Minor Losses 1mahesh100% (1)
- Unit Iv Boundary Layer: Sri Vidya College of Engineering & Tech Question Bank-Unit - IvDokumen7 halamanUnit Iv Boundary Layer: Sri Vidya College of Engineering & Tech Question Bank-Unit - IvBahman JadidiBelum ada peringkat
- ME 363 - Fluid MechanicsDokumen5 halamanME 363 - Fluid MechanicsCristobal MendozaBelum ada peringkat
- Head Loss Lab ReportDokumen15 halamanHead Loss Lab ReportMajak MarialBelum ada peringkat
- Sistem Instalasi MekanikalDokumen156 halamanSistem Instalasi MekanikalDharmestha DewantoroBelum ada peringkat
- Hydraulics II Unit 3Dokumen62 halamanHydraulics II Unit 3Eyob Light WorkuBelum ada peringkat
- Computational HydraulicsDokumen404 halamanComputational HydraulicsTesfaye NegasaBelum ada peringkat
- Lecture-7-Energy Consideration+OrificesDokumen49 halamanLecture-7-Energy Consideration+OrificesAbdul Waseh BhangooBelum ada peringkat
- Lect 02 2020Dokumen8 halamanLect 02 2020Hukry AingBelum ada peringkat
- Lecture 5 2Dokumen15 halamanLecture 5 2IbrahimDewaliBelum ada peringkat
- MA3006 Tutorial 7 SolutionDokumen4 halamanMA3006 Tutorial 7 Solutionclarence limBelum ada peringkat
- Cornish MethodDokumen30 halamanCornish MethodEverlasting MemoriesBelum ada peringkat
- Chapter-12 PumpDokumen39 halamanChapter-12 PumpSalehin AnamBelum ada peringkat
- CH 3 2020Dokumen62 halamanCH 3 2020Emmanuel LazoBelum ada peringkat
- Pipe Flow: Laminar Flow or Viscous FlowDokumen34 halamanPipe Flow: Laminar Flow or Viscous FlowBalaguruBelum ada peringkat
- Notes Ce 503 Fluid Mechanics 2 Unit 2Dokumen18 halamanNotes Ce 503 Fluid Mechanics 2 Unit 2HyperHimansh SharmaBelum ada peringkat
- Flow in Circular Pipes: ObjectiveDokumen25 halamanFlow in Circular Pipes: ObjectivePatrickAndradeBelum ada peringkat
- Flow Through PipesDokumen29 halamanFlow Through PipesMichael TinambunanBelum ada peringkat
- Pressure Losses in Pipe Network Name: University: CodeDokumen7 halamanPressure Losses in Pipe Network Name: University: CodeshagsBelum ada peringkat
- FMHM Unit-Iii Part 2 Class NotesDokumen73 halamanFMHM Unit-Iii Part 2 Class Notes203C310 ChandanBelum ada peringkat
- Flow in ConduitsDokumen29 halamanFlow in ConduitsEngr Sabiul AlamBelum ada peringkat
- Physical Electronics: Handbook of Vacuum PhysicsDari EverandPhysical Electronics: Handbook of Vacuum PhysicsA. H. BeckBelum ada peringkat
- Gambar II Got MiringDokumen1 halamanGambar II Got MiringSandro Nainggolan BrabBelum ada peringkat
- 2014: Product Keys For Autodesk Products: Product Name Product KeyDokumen5 halaman2014: Product Keys For Autodesk Products: Product Name Product KeySandro Nainggolan BrabBelum ada peringkat
- Soundering Test Soil InvestigationDokumen2 halamanSoundering Test Soil InvestigationSandro Nainggolan BrabBelum ada peringkat
- GridDataReport Cobacoba1Dokumen7 halamanGridDataReport Cobacoba1Sandro Nainggolan BrabBelum ada peringkat
- MATERI - 2 Saluran Komposite & GabunganDokumen14 halamanMATERI - 2 Saluran Komposite & GabunganSandro Nainggolan BrabBelum ada peringkat
- 9860 New CodeDokumen1 halaman9860 New CodeSandro Nainggolan BrabBelum ada peringkat
- Siklus RankineDokumen26 halamanSiklus RankineArialdi Almonda0% (1)
- Smith Meter VDR Vertical Deaerator SpecificationsDokumen8 halamanSmith Meter VDR Vertical Deaerator SpecificationsClarkFedele27Belum ada peringkat
- Mechanical Engineering Hydraulic Mechanics Important MCQ PDFDokumen11 halamanMechanical Engineering Hydraulic Mechanics Important MCQ PDFGaneshBelum ada peringkat
- AnandaSelig 2018 AIAA Paper 2018 0310 BirdAirfoilDesignDokumen21 halamanAnandaSelig 2018 AIAA Paper 2018 0310 BirdAirfoilDesignlucifer morningstarBelum ada peringkat
- 3.10.E.pv25G Pneumatic Control Valves DN15-100-EnDokumen6 halaman3.10.E.pv25G Pneumatic Control Valves DN15-100-EnSon Trinh PhuongBelum ada peringkat
- Accumulator Unloading Valve, Type MRQADokumen2 halamanAccumulator Unloading Valve, Type MRQALibinBelum ada peringkat
- MSS SP 61-Pressure Testing of ValvesDokumen10 halamanMSS SP 61-Pressure Testing of ValvesharishcsharmaBelum ada peringkat
- Uick Reference: FILE NO.: A11-005Dokumen52 halamanUick Reference: FILE NO.: A11-005TagelBelum ada peringkat
- Shigley 9E SI Chap12Dokumen26 halamanShigley 9E SI Chap12Yann YeuBelum ada peringkat
- Types of Water Closet: Siphon-VortexDokumen2 halamanTypes of Water Closet: Siphon-VortexMherlieBelum ada peringkat
- BookssssDokumen2 halamanBookssssAnmol RatnaBelum ada peringkat
- Compressible Flow - Water HammerDokumen7 halamanCompressible Flow - Water Hammersiroliver39Belum ada peringkat
- Orifice Flowmeter Straight RunDokumen4 halamanOrifice Flowmeter Straight RunMuhammad ImranBelum ada peringkat
- Chapter 3:first Law of Thermodynamics and Its ProcessesDokumen24 halamanChapter 3:first Law of Thermodynamics and Its ProcessesDaneal FikriBelum ada peringkat
- Design Calculation of Penstock and Nozzle For 5kW Pelton TurbineDokumen3 halamanDesign Calculation of Penstock and Nozzle For 5kW Pelton TurbineSahil AcharyaBelum ada peringkat
- Hidrometro ARADDokumen2 halamanHidrometro ARADcybermineBelum ada peringkat
- Pressure Control ValveDokumen38 halamanPressure Control ValvePrasanna KumarBelum ada peringkat
- Aerody Practice ProbDokumen2 halamanAerody Practice Probmadjeaudrei.romeroBelum ada peringkat
- Irrigation Manual W-22Dokumen38 halamanIrrigation Manual W-22zoheb ahmedBelum ada peringkat
- 3-1-Unit IIDokumen40 halaman3-1-Unit IIGroup-4 CommonBelum ada peringkat
- Practice Questions PneumaticsDokumen13 halamanPractice Questions Pneumaticssamer07hd100% (3)
- Experiment 7 - Flow Over A V-NotchDokumen14 halamanExperiment 7 - Flow Over A V-NotchMd TareqBelum ada peringkat