Hydrostatic Forces On A Curved Surface
Diunggah oleh
aadhanDeskripsi Asli:
Judul Asli
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Hydrostatic Forces On A Curved Surface
Diunggah oleh
aadhanHak Cipta:
Format Tersedia
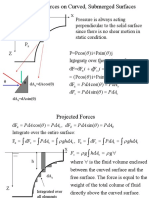
Hydrostatic Forces on Curved, Submerged Surfaces
Pressure is always acting
perpendicular to the solid surface
since there is no shear motion in
static condition.
P
P
x
P
z
x
Z
u
x
x
P=Pcos( )i+Psin( )j
Integrate over the entire surface
dF=dF
(Pcos( )i+Psin( )j)dA
dF cos( )
sin( )
z
x
z z
i dF j PdA
PdA PdA
dF PdA PdA
u u
u u
u
u
+ =
=
= =
= =
u
u
dA
x
=dAcos(u)
dA
z
=dAsin(u)
Projected Forces
x
x z
dF cos( ) , sin( )
Integrate over the entire surface:
F , F
x Z Z
x x x z z z
PdA PdA dF PdA PdA
dF PdA ghdA dF PdA ghdA
u u
= = = =
= = = = = =
} } } } } }
x
Z
Integrated over
all elements
h
dA
z
where is the fluid volume enclosed
between the curved surface and the
free surface. The force is equal to the
weight of the total colume of fluid
directly above the curved surface.
The li
z z
F g hdA g = =
}
ne action passes through the
center of gravity of the volume
of liquid being displaced.
Buoyancy
Force acting down F
D
= gV
1
from
Force acting up F
U
= gV
2
from
Buoyancy = F
U
-F
D
=g(V
2
-V
1
)=gV
V: volume occupied by the object
Horizontal Forces
x
Z
Integrated over
all elements
h
dA
z
x
F
x x x
dF PdA ghdA = = =
} } }
h
dA
x
Equivalent system:
A plane surface perpendicular
to the free surface
Projected
area A
x
Finding F
x
is to determine the force acting
on a plane submerged surface oriented
perpendicular to the surface. A
x
is the
projection of the curved surface on the yz
plane. Similar conclusion can be made to
the force in the y direction F
y
.
x
F
x x x
dF PdA ghdA = = =
} } }
Examples
Determine the magnitude of the resultant force acting on the hemispherical surface.
2 m R=0.5 m
z
x
x
x
2 2
x
F
A is the projection of the sphere along the x direction
and it has a shape of a circle A = (0.5) 0.785( )
(1000)(9.8)(2)(0.785) 15386( )
( )
(1000)
x x C x
x
z z z
PdA g ydA gh A
m
F N
F PdA g zdA g g
t
+
= = =
=
= =
= = = =
=
} }
} }
( ) ( )
3
1 4
(9.8) 2564( )
2 3
R N t =
minus equals
15386 2564
The line of action of the force
must go through the center of the
hemisphere, O (why?)
x z
F F i F k i k = + =
Line of Action
Horizontal direction: line of action goes through z
z
z
C
4
2
4
' (2)
(2)
2.03125( )
xx
C
C
R
I
z z
Az R
m
t
t
= + = +
=
Vertical direction: the line of action is 3R/8
away from the center of the hemisphere
Projection
in x-direction
location of the centroid for a hemisphere
is 3R/8=0.1875(m) away from the equator plane
The resultant moment of both forces with respect to the
center of the hemisphere should be zero:
F
x
(2.03125-2)-F
z
(0.1875)
=15386(0.03125)-2564(0.1875)=0
z
Anda mungkin juga menyukai
- Hydrostatic Forces On A Curved SurfaceDokumen6 halamanHydrostatic Forces On A Curved SurfaceRye AnBelum ada peringkat
- 022 Static Surface ForcesDokumen54 halaman022 Static Surface ForcesAhmad Haikal Mohd HalimBelum ada peringkat
- Submerged Body, Center of Pressure and BuoyancyDokumen44 halamanSubmerged Body, Center of Pressure and BuoyancyAnish PathakBelum ada peringkat
- HydrostaticDokumen9 halamanHydrostaticRezza AdityaBelum ada peringkat
- Hydrostatic Forces On A Curved SurfaceDokumen6 halamanHydrostatic Forces On A Curved SurfaceKim Luigi GondaBelum ada peringkat
- 2013 Lect6 FORCES ON PIPE BENDSDokumen39 halaman2013 Lect6 FORCES ON PIPE BENDSBagus PrakasaBelum ada peringkat
- Fluid Mechanics Lecture - HydrostaticsDokumen15 halamanFluid Mechanics Lecture - HydrostaticsBernardo FariasBelum ada peringkat
- 3695 Sutardi Fluid Statics 02Dokumen19 halaman3695 Sutardi Fluid Statics 02Ruben Edhino Vicente DueñasBelum ada peringkat
- Chap 3 Sec2 PDFDokumen17 halamanChap 3 Sec2 PDFteknikpembakaran2013Belum ada peringkat
- Tutorial 1 ExplanationDokumen14 halamanTutorial 1 Explanation木辛耳总Belum ada peringkat
- 022 Static Surface Forces (1) SDokumen54 halaman022 Static Surface Forces (1) SMayur PatelBelum ada peringkat
- CE374-Ch2a - Ek (Compatibility Mode)Dokumen59 halamanCE374-Ch2a - Ek (Compatibility Mode)Ruben Edhino Vicente DueñasBelum ada peringkat
- Hydrostatic ForceDokumen9 halamanHydrostatic ForceUMESH SINGHBelum ada peringkat
- Chap 3 Sec2Dokumen24 halamanChap 3 Sec2ZewdieBelum ada peringkat
- Southern Methodist University Bobby B. Lyle School of Engineering ENCE/ME 2342 Fluid Mechanics Roger O. Dickey, PH.D., P.EDokumen59 halamanSouthern Methodist University Bobby B. Lyle School of Engineering ENCE/ME 2342 Fluid Mechanics Roger O. Dickey, PH.D., P.EKenneth KnowlesBelum ada peringkat
- Phy30s Review MRDokumen6 halamanPhy30s Review MRapi-683027695Belum ada peringkat
- MM301 2 Fluid Statics-UpdatedDokumen32 halamanMM301 2 Fluid Statics-UpdatedoddomancanBelum ada peringkat
- Gradient Div CurlDokumen46 halamanGradient Div CurlDivyanshuVermaBelum ada peringkat
- Hydrostatics Nature of Forces: Governing Equation For Pressure Field - IDokumen8 halamanHydrostatics Nature of Forces: Governing Equation For Pressure Field - ItmcoachingcentreBelum ada peringkat
- CHEQDokumen69 halamanCHEQArmindo JoséBelum ada peringkat
- Chapter 3 Fluid StatisticsDokumen50 halamanChapter 3 Fluid Statisticsdist2235Belum ada peringkat
- Summary Mona ShalanDokumen39 halamanSummary Mona Shalanromaehab201912Belum ada peringkat
- L - 09 - Inclined Plane SurfaceDokumen20 halamanL - 09 - Inclined Plane SurfaceAllen PaulBelum ada peringkat
- MVU AP Physics Equations 1st SemesterDokumen3 halamanMVU AP Physics Equations 1st SemesterEvan ScottBelum ada peringkat
- Hydrostatic ForcesDokumen32 halamanHydrostatic ForcesislamBelum ada peringkat
- CurveDokumen19 halamanCurveSheryll de GuzmanBelum ada peringkat
- Hydrostatic Force: Fluids, Incompressible or Not, at RestDokumen7 halamanHydrostatic Force: Fluids, Incompressible or Not, at RestFirdaus DausBelum ada peringkat
- Hydrostatic Force On A Plane Surface: Henryk KudelaDokumen4 halamanHydrostatic Force On A Plane Surface: Henryk KudelaSheryll de GuzmanBelum ada peringkat
- PDF Tutorial On A Fluid Mechanics QuestionDokumen3 halamanPDF Tutorial On A Fluid Mechanics QuestionAnas Abdel RihemBelum ada peringkat
- Forces On Submerged SurfacesDokumen15 halamanForces On Submerged SurfacesSuneel VasandaniBelum ada peringkat
- Forces On Curved Surfaces: 7.1 Alternative Method For Plane Inclined SurfacesDokumen7 halamanForces On Curved Surfaces: 7.1 Alternative Method For Plane Inclined SurfacesMohamed AddanBelum ada peringkat
- Hydrostatic Thrust On Submerged SurfacesDokumen30 halamanHydrostatic Thrust On Submerged SurfacesShyam Pandey0% (1)
- I F C F: Pure Math SummaryDokumen4 halamanI F C F: Pure Math SummaryRuijia ZengBelum ada peringkat
- Fluid Mechanics - AS102: Class Note No: 10Dokumen31 halamanFluid Mechanics - AS102: Class Note No: 10Pranav KulkarniBelum ada peringkat
- Hydrostatic Force On Curved Submerged Surfaces: A PD FDokumen11 halamanHydrostatic Force On Curved Submerged Surfaces: A PD Fgs__10Belum ada peringkat
- CH 4 - Principles of Power SystemDokumen19 halamanCH 4 - Principles of Power SystemAqsa KhanamBelum ada peringkat
- 13-Surface Integrals - Part 2Dokumen10 halaman13-Surface Integrals - Part 2Mohd Afiq AminBelum ada peringkat
- Fluid Mechanics: DR Farid KhanDokumen18 halamanFluid Mechanics: DR Farid KhanShadmƛn RƛzzƛqBelum ada peringkat
- Fluid StatisticsDokumen66 halamanFluid Statisticskonetinarendra100% (1)
- Person Note Document For Multivariable CalculusDokumen2 halamanPerson Note Document For Multivariable CalculusImcomingforyouBelum ada peringkat
- The Momentum EquationDokumen11 halamanThe Momentum EquationLutfi IsmailBelum ada peringkat
- Cheat SheetDokumen2 halamanCheat SheetJeet TrivediBelum ada peringkat
- 2012 09 02-L2 3-ReifenbergerDokumen12 halaman2012 09 02-L2 3-Reifenbergerbenchang93Belum ada peringkat
- Module 2Dokumen36 halamanModule 2swathiaabidBelum ada peringkat
- Lecture-4-Hydrostatic Force On Submerged BodiesDokumen40 halamanLecture-4-Hydrostatic Force On Submerged BodiesSyed WasimBelum ada peringkat
- Fluid Flow in Solidification 2Dokumen8 halamanFluid Flow in Solidification 2Anonymous T02GVGzBBelum ada peringkat
- Fluid Mechanics: EIT ReviewDokumen33 halamanFluid Mechanics: EIT ReviewSharath ChandraBelum ada peringkat
- S2 Module 2 HandoutDokumen19 halamanS2 Module 2 HandoutAakanksha KartikBelum ada peringkat
- Module 3 Hydrostatic Forces & BuoyancyDokumen9 halamanModule 3 Hydrostatic Forces & BuoyancyJuan HeroBelum ada peringkat
- Blasius TheoremDokumen9 halamanBlasius TheoremAhmed Assaf100% (1)
- Example Problems of Potential FlowDokumen5 halamanExample Problems of Potential FlowShiva HarshBelum ada peringkat
- Hydrostatic ForcesDokumen13 halamanHydrostatic ForcesPritz Jay Magno TorresBelum ada peringkat
- Calc Study PDFDokumen7 halamanCalc Study PDFRussell FromUpBelum ada peringkat
- Elastic Constants Relation (E, G & K Relation) Strength of Materials Ravi Kumar KDokumen19 halamanElastic Constants Relation (E, G & K Relation) Strength of Materials Ravi Kumar KkunkalamarruBelum ada peringkat
- Appendix 11.1 More On Boundary Conditions: Simple Example of Moving BoundaryDokumen22 halamanAppendix 11.1 More On Boundary Conditions: Simple Example of Moving BoundaryArushi JainBelum ada peringkat
- The Plasma Dispersion Function: The Hilbert Transform of the GaussianDari EverandThe Plasma Dispersion Function: The Hilbert Transform of the GaussianPenilaian: 5 dari 5 bintang5/5 (1)
- Introductory Differential Equations: with Boundary Value Problems, Student Solutions Manual (e-only)Dari EverandIntroductory Differential Equations: with Boundary Value Problems, Student Solutions Manual (e-only)Belum ada peringkat
- S3 VMRDokumen12 halamanS3 VMRaadhanBelum ada peringkat
- SpiceJet - E-Ticket - PNR J2CT7Y - 23 Nov 2015 Chennai-Delhi For MRS. KANAGARAJDokumen2 halamanSpiceJet - E-Ticket - PNR J2CT7Y - 23 Nov 2015 Chennai-Delhi For MRS. KANAGARAJaadhanBelum ada peringkat
- Bharat Sanchar Nigam Limited: Receipt DetailsDokumen1 halamanBharat Sanchar Nigam Limited: Receipt DetailsaadhanBelum ada peringkat
- Mech Syllabus PDFDokumen162 halamanMech Syllabus PDFaadhanBelum ada peringkat
- Design of Machine ElementsDokumen53 halamanDesign of Machine ElementsSrks Kondal Reddy100% (2)
- DTS PDFDokumen18 halamanDTS PDFaadhan100% (1)
- Design of Machine ElementsDokumen53 halamanDesign of Machine ElementsSrks Kondal Reddy100% (2)
- Dynamics of Machinery PDFDokumen18 halamanDynamics of Machinery PDFThomas VictorBelum ada peringkat
- Design of Machine ElementsDokumen53 halamanDesign of Machine ElementsSrks Kondal Reddy100% (2)
- Dynamics of Machinery PDFDokumen18 halamanDynamics of Machinery PDFThomas VictorBelum ada peringkat
- P-103 Engineering Graphics Lab: DATE: 26-12-2013 TIME: 09.30AM - 12.30 PMDokumen3 halamanP-103 Engineering Graphics Lab: DATE: 26-12-2013 TIME: 09.30AM - 12.30 PMaadhanBelum ada peringkat
- Classificaitons of Fluid MachinesDokumen4 halamanClassificaitons of Fluid MachinesaadhanBelum ada peringkat
- Goal 6 Unesco Water SanatationDokumen5 halamanGoal 6 Unesco Water Sanatationapi-644347009Belum ada peringkat
- North Central Mindanao College: Maranding, Lala, Lanao Del NorteDokumen8 halamanNorth Central Mindanao College: Maranding, Lala, Lanao Del NorteAnalyn FielBelum ada peringkat
- LINEAR INDUCTION MOTOR 6981660.ppsxDokumen56 halamanLINEAR INDUCTION MOTOR 6981660.ppsxFalley FasterBelum ada peringkat
- Geology of Johannesburg ReadingDokumen2 halamanGeology of Johannesburg ReadingKavish DayaBelum ada peringkat
- DLP Physical Science Week1Dokumen2 halamanDLP Physical Science Week1gizellen galvezBelum ada peringkat
- South Valley University Faculty of Science Geology Department Dr. Mohamed Youssef AliDokumen29 halamanSouth Valley University Faculty of Science Geology Department Dr. Mohamed Youssef AliHari Dante Cry100% (1)
- Introduction: Science and Environment: Brgy - Pampang, Angeles City, PhilippinesDokumen65 halamanIntroduction: Science and Environment: Brgy - Pampang, Angeles City, PhilippinesLance AustriaBelum ada peringkat
- MetDokumen41 halamanMetadityaBelum ada peringkat
- EU - Guidance On GMP For Food Contact Plastic Materials and Articles (60p)Dokumen60 halamanEU - Guidance On GMP For Food Contact Plastic Materials and Articles (60p)Kram NawkBelum ada peringkat
- Qa/Qc Mechanical Monthly Progress Report For June 2015: Area/System Description Status RemarksDokumen1 halamanQa/Qc Mechanical Monthly Progress Report For June 2015: Area/System Description Status RemarksRen SalazarBelum ada peringkat
- NREL Novel Electrolyzer Applications Providing More Than Just Hydrogen PDFDokumen35 halamanNREL Novel Electrolyzer Applications Providing More Than Just Hydrogen PDFJosePPMolinaBelum ada peringkat
- HACH LANGE Amino Acid F Reagent Powder (2353255)Dokumen6 halamanHACH LANGE Amino Acid F Reagent Powder (2353255)kerem__22Belum ada peringkat
- CM Bu9000 Eng Bushings 3Dokumen36 halamanCM Bu9000 Eng Bushings 3ing.dmanriq27100% (1)
- 3592 Operator GuideDokumen103 halaman3592 Operator GuideNaim GhattasBelum ada peringkat
- Biasing Opamps Into Class ADokumen11 halamanBiasing Opamps Into Class AsddfsdcascBelum ada peringkat
- Mechanism Design: A SeriesDokumen3 halamanMechanism Design: A Seriesamirmasood kholojiniBelum ada peringkat
- 1943 Dentures Consent FormDokumen2 halaman1943 Dentures Consent FormJitender ReddyBelum ada peringkat
- Accessories 162-USDokumen20 halamanAccessories 162-USعايد التعزيBelum ada peringkat
- Editor: Lalsangliana Jt. Ed.: H.Dokumen4 halamanEditor: Lalsangliana Jt. Ed.: H.bawihpuiapaBelum ada peringkat
- Pediatric Gynecology BaruDokumen79 halamanPediatric Gynecology BaruJosephine Irena100% (2)
- Chapter 01Dokumen16 halamanChapter 01deepak_baidBelum ada peringkat
- The Gingerbread Man-1 EnglishareDokumen40 halamanThe Gingerbread Man-1 EnglishareamayalibelulaBelum ada peringkat
- Outerstellar Self-Impose RulesDokumen1 halamanOuterstellar Self-Impose RulesIffu The war GodBelum ada peringkat
- BCSL 058 Previous Year Question Papers by IgnouassignmentguruDokumen45 halamanBCSL 058 Previous Year Question Papers by IgnouassignmentguruSHIKHA JAINBelum ada peringkat
- Sandvik Saf 31803 Tube and Pipe, Seamless: DatasheetDokumen9 halamanSandvik Saf 31803 Tube and Pipe, Seamless: DatasheetPaul NeedhamBelum ada peringkat
- Commercial Kitchen Fire InvestigationsDokumen6 halamanCommercial Kitchen Fire InvestigationsBen ConnonBelum ada peringkat
- Benefits of OTN in Transport SDNDokumen9 halamanBenefits of OTN in Transport SDNGhallab AlsadehBelum ada peringkat
- Psalm151 160Dokumen3 halamanPsalm151 160Gina KristenBelum ada peringkat
- Pantalla Anterior Bienvenido: Cr080vbesDokumen3 halamanPantalla Anterior Bienvenido: Cr080vbesJuan Pablo Virreyra TriguerosBelum ada peringkat
- Instructor: DR - Ashok Kaushal: Orthogonal ViewsDokumen49 halamanInstructor: DR - Ashok Kaushal: Orthogonal ViewsKristi GjokaBelum ada peringkat