Torsional Vibration of Beams: Torsional Vibrations of Aircraft Wings Can Be Closely Modeled As Torsional Vibrations of Cantilevered Beams

SCHOOL OF MECHANICAL AND
AEROSPACE ENGINEERING
NANYANG TECHNOLOGICAL
UNIVERSITY, SINGAPORE
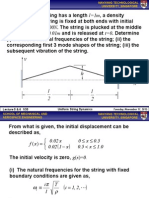
TORSIONAL VIBRATION OF BEAMS:

Torsional vibrations of aircraft wings can be closely
modeled as torsional vibrations of cantilevered beams.
z
x
y
l
y
Lectures 7 & 8
1/35
Torsional Vibration of Beams
Sunday, August 30, 2015

Equations of Motion:
T
2
T
y T I Py 2
y
t
T
2
IP 2
y
t
(1)
T
Mass Polar Moment

of Inertia Ip:
IP
T GI P
Lectures 7 & 8
x 2 z 2 dA
2/35
(2)
T
y
y
Elemental
strip
2
2
GI P 2 I P 2
y
t
(3)

Solution of Torsional Vibrations:
2
2
GI P 2 I P 2
y
t
(3)
( : kg / m 3 )
Based on Separation of Variables method, the solution

of satisfies (3) can be written as,
y, t X y Y t
Then,
(4)
2
2
2 X y
2 X y Y t
Y t X y Y t X Y
2
2
y
y
y
2
2
2Y t
t X Y
X
y
Y
t
X
y
X
y
Y
t 2
t 2
t 2
Lectures 7 & 8
3/35

Substitute them into (3), we have

GI X Y I X Y
P
(5)
Equation (5) can be further written as,

X Y
(6)
X
G Y
Examine equation (6), the LHS is a function of y only
while the RHS is a function of t only. If they can be
equal, both sides must be equal to a CONSTANT:
X
Y
2
(7)
X
G Y
Lectures 7 & 8
4/35
X 2 X 0
Y 2 G Y 0
(8a)
(8b)

The general solutions of (8a) and (8b) are,
X y A sin y B cos y
Y t C sin
G
t D cos

(9a)
G
t

(9b)
Constants A and B can be determined from the

boundary conditions at the ends of the beam, and C
and D can be found as functions of the given initial
beam torsional deflection and initial torsional velocity,
as will be shown in the examples followed.
Lectures 7 & 8
5/35

EX ClampedFree: A uniform circular beam of length

l=1m and diameter d=10cm is clamped at one end and is
subjected to a torque T=9000Nm at the other end. Shear
modulus G is assumed to be G=91010 N/m2 and density
=7800kg/m3. The applied torque is then suddenly
released (at t=0), determine the subsequent torsional
vibration of the beam.
Lectures 7 & 8
6/35

Free Vibration Analysis No Force/Torque Considered!

The boundary condition for clamped end becomes:
0, t 0
(10a)
For the free end, there is no torque applied (Free Vibration

Analysis),
T G IP
Lectures 7 & 8
7/35
T l G IP
l , t
0
y
l , t 0
(10b)

Recall the general solutions,
X y A sin y B cos y
Y t C sin
(9a)
G
t D cos

G
t

(9b)
So, general solution for becomes,
y, t X y Y t
A sin y B cos y C sin
Lectures 7 & 8
8/35
G
t D cos

G
t


Apply boundary condition at y=0:
0, t X 0 Y t 0
X 0 0
A sin 0 B cos 0 0
B 0
Update X(y) to become,
X y A sin y
X y A cos y
Apply boundary condition at y=l:
l , t X l Y t 0
A cos l 0
l
Lectures 7 & 8
9/35
2i 1
2
X l 0
cos l 0

2i 1
2l
1, 2,

Hence, the natural frequencies of torsional vibration

of a clamped-free beam become,
i i
G
2i 1
2l
i 1, 2,
Substitute known parameters, i becomes
i 5335.7 2i 1
i 1, 2,
Since X(y) represents the vibration mode shape,
X y A sin y
Hence mode shapes are,
y sin
Lectures 7 & 8
10/35
2i 1 y
2l
i 1, 2,

Clamped-Free Beam Torsional Vibration Mode Shapes

Lectures 7 & 8
11/35

The general solution for can now be updated to become,
y, t X y Y t
sin
i 1
2i 1y E
2l
i sin
5335.7 2i 1 t Fi cos 5335.7 2i 1 t
The initial displacement condition:

The initial displacement under constant torque becomes,
Tl l
9000 1
0 l
0.0102 rad
1
GI P
10
9 10 3.14159 0.14
32
Hence,
Lectures 7 & 8
y , 0 0.0102 y
12/35
rad

The initial velocity condition:

The initial velocity is assumed to be zero,
y , 0 0
Substitute initial displacement condition,
y, 0 X y Y 0
i 1
2i 1y
E
sin
i sin
2l
2i 1y
F sin
i 1
Lectures 7 & 8
2l
13/35
5335.7 2i 1 0 Fi cos 5335.7 2i 1 0
0.0102 y

So, the initial displacement condition leads us to,
2i 1y
F sin
i
i 1
0.0102 y
(11)
Multiply (11) by sin[(2j-1)y/2] and integrate over the

length,
0
i 1
2i 1y sin 2 j 1y dy
F sin
i
0.0102 y sin
2 j 1y dy
2
Based on the orthognality properties of mode shapes,
Fi 0.0204
Lectures 7 & 8
14/35
2i 1y
y sin
dy 1 i 1
2
0.0816
2i 1
2 2
i 1, 2,

Torsional velocity becomes,
y , t X y Y t
2i 1y
sin
5335.7 2i 1
2l
Ei cos 5335.7 2i 1 t Fi sin 5335.7 2i 1 t
i 1
Substitute initial velocity condition,
i 1
5335.7 2i 1 Ei
2i 1y
sin
2
(12)
Multiply (12) by sin[(2j-1)y/2] and integrate over the

length,
Ei 0 i 1, 2,
Lectures 7 & 8
15/35

Hence, the final solution becomes,
y, t
Lectures 7 & 8
i 1
16/35
0.0816
0.0816 1 i 1
2 2i 1 2
2i 1y
sin
cos 5335.7 2i 1 t
2

Natural Frequencies and Mode Shapes of Other

Boundary Conditions - Clamped-Clamped:
The boundary conditions for Clamped-Clamped case,
0, t l , t 0
(13a, 13b)
Applying the first boundary condition at y=0 leads to,
0, t X 0 Y t 0
A sin 0 B cos 0 0
X 0 0
B 0
Update the solution of X,
X y A sin y
Lectures 7 & 8
17/35

Applying the second boundary condition at y=l leads to,
l, t X l Y t 0
A sin l 0
l i
X l 0
sin l 0 ( Why not A 0 ? )
i 1, 2,
Therefore, natural frequencies are given by,
i i
G
i
i 1, 2,
Mode shapes are given by,
iy
i y sin y sin
l
Lectures 7 & 8
18/35
i 1, 2,

Clamped-Clamped Beam Torsional Vibration Mode Shapes

Lectures 7 & 8
19/35

Free-Free Boundary
Conditions:
The boundary conditions for Free-Free case,
0, t l , t 0
(14a, 14b)
(No torques)
0, t X 0 Y t 0
X 0 0
X y A sin y B cos y
X y A cos y B sin y
X 0 0 A cos 0 B sin 0 0
X y B cos y
Lectures 7 & 8
20/35
A0
X y B sin y

l , t X l Y t 0
B sin l 0
l i
X l 0
sin l 0
OR
i 0, 1, 2,
Therefore, natural frequencies are given by,
i i
G
i
i 0, 1, 2,
Mode shapes are given by,
iy
i y cos y cos
l
Lectures 7 & 8
21/35
i 0, 1, 2,

When i=0 (=0), 0=0 is called Rigid Body mode. The

corresponding mode shape of a rigid body mode is a
constant:
0 y cos 0 1
Lectures 7 & 8
22/35

Free-Free Beam Torsional Vibration Mode Shapes

Lectures 7 & 8
23/35

EX ClampedFree: A uniform circular beam of length

l=1m and diameter d=10cm is clamped at one end and is
subjected to a torque Tl(t)=5000sin2000t Nm. Also, a
continuously distributed torque q(y, t)=8000sin2000t N is
applied along the beam. Shear modulus G is assumed to
be G=91010 N/m2 and density =7800kg/m3. Determine the
torsional vibration of the beam.
Lectures 7 & 8
24/35

The generalized torque becomes
i t
l
0
F y , t i y dy
l
0
l
0
2i 1y
2l
T0 sin t y l sin
2i 1y
q0 sin t sin
dy
dy
2l
2q0 l
i 1
sin t
1 T0 sin t
2i 1
Where, T0 5000 Nm, q0 8000 N , 2000 rad / s, l 1m.
Recall the equation for i-th generalized coordinate,
l
l 2
i t
i i t i t
(Vibration of Strings)
2
2
l I P
l I P 2
i t
i i t i t (Beam Torsional Vib)
2
2
Lectures 7 & 8
25/35

To simplify, let
2
2q0l
i 1
1 T0
T i
2i 1
l IP
Then,
i t i2 i t T i sin t
The corresponding general solution becomes,

T i
i t Ai sin i t Bi cos i t 2
sin t
2
i
So, the solution can be written,
y, t
i y i t
i 1
T i
2i 1y
sin
sin t
Ai sin i t Bi cos i t 2
2
2l
i

i 1
Lectures 7 & 8
26/35

Consider the initial displacement,
2i 1y
y , 0 0 sin
Bi 0 Bi 0 i 1,2,
2l
i 1
(Previously discussed)
Consider the initial velocity,
T
i
Aii cos i t Bii sin i t
cos
2
2
i 1
i
T i
2i 1y
0
y , 0 0 sin
Aii 2
2
2l
i

i 1
Multiply both sides by sin((2j-1)y/2l) and integrate over [0, l],
y , t
i 1
2i 1y
sin
2l
F
i
Aii
2
2
Lectures 7 & 8
27/35
l
0
2i 1y
2 j 1y
sin
sin
dy 0
2l
2l

Aii T i
2
2
2 0
T i
Ai
i (i2 2 )
y, t
i 1
i 1, 2,
i 1, 2,
T i
2i 1y
sin
2
2
2l
i
sin t
sin i t
i
Substitute known values,
i 5335.7 2i 1
i 1, 2,
2000 rad / s
Lectures 7 & 8
28/35

2
2q0l
i 1
1 T0
T i
2i 1
l IP
2
6
7800 1 9.82 10
1.306 10 1
5
y, t
i 1
i 1
5000 1
i 1
1.330 10 5
2i 1
1
i2 4 10 6
5
1
.
330
10
i 1
5
1
.
306
10
2i 1
2i 1y
sin
where, i 5335.7 2i 1
Lectures 7 & 8
29/35
5093
2i 1
2000
sin 2000t
sin i t
i
i 1, 2,

Natural Frequencies and Mode Shapes of Torsional Beam

on Elastic Support:
The boundary condition at y=0 becomes,
0, t 0
y , t X y Y t
(15a)
y , t X y Y t
At y=l, apply the moment equation,
G I P l , t kT l , t G I P X l kT X l
Lectures 7 & 8
30/35
(15b)

0, t X 0 Y t 0
A sin 0 B cos 0 0
X 0 0
B 0
X y A sin y
X y A cos y
G I P X l kT X l
G I P A cos l kT A sin l
kT l
l cos(al )
sin l (16)
G IP
Define a dimensionless support parameter as,
G IP
kT
Lectures 7 & 8
31/35

Then, equation (16) becomes,
sin l l cos l 0
This transcendental
equation has infinite
set of roots which
cannot be found in
closed form.
However, for any
given value of
support parameter ,
can be solved from
(17) numerically. The
first 4 il (i=1,2,3,4)
are shown:
Lectures 7 & 8
32/35
(17)
l versus

When = 0, it is the case of Clamped-Free boundary

conditions and when , it becomes a case of
Clamped-Clamped boundary conditions we have
discussed. Hence, the curves start with il values
corresponding to Clamped-Free case and approach
values of the Clamped-Clamped case as becomes large.
Having computed the values of i (i=1,2,), the
corresponding natural frequencies of the elastically
supported beam become,
i i
i 1, 2,
(18)
And the mode shapes become,
i y sin i y
Lectures 7 & 8
33/35
i 1, 2,
(19)

Mode Shapes of Elastically Supported Beam =1.0

NB: These mode shapes are no longer orthogonal !!
Lectures 7 & 8
34/35

SUMMARY
1.
Governing differential equation for torsional

vibration of beam has been developed;
2.
Torsional vibration natural frequencies and
mode
shapes have been derived based on
Separation of Variable;
3.
Various boundary conditions have been
investigated to establish vibration properties;
4.
Free and forced torsional vibration analyses
have been studied.
Lectures 7 & 8
35/35

Torsional Vibration of Beams: Torsional Vibrations of Aircraft Wings Can Be Closely Modeled As Torsional Vibrations of Cantilevered Beams

Diunggah oleh

Informasi Dokumen

Judul Asli

Hak Cipta

Format Tersedia

Bagikan dokumen Ini

Bagikan atau Tanam Dokumen

Opsi Berbagi

Apakah menurut Anda dokumen ini bermanfaat?

Apakah konten ini tidak pantas?

Hak Cipta:

Format Tersedia

Torsional Vibration of Beams: Torsional Vibrations of Aircraft Wings Can Be Closely Modeled As Torsional Vibrations of Cantilevered Beams

Diunggah oleh

Hak Cipta:

Format Tersedia

SCHOOL OF MECHANICAL AND