Thermal Strains and Element of The Theory of Plasticity
Diunggah oleh
이희영Deskripsi Asli:
Judul Asli
Hak Cipta
Format Tersedia
Bagikan dokumen Ini
Apakah menurut Anda dokumen ini bermanfaat?
Apakah konten ini tidak pantas?
Laporkan Dokumen IniHak Cipta:
Format Tersedia
Thermal Strains and Element of The Theory of Plasticity
Diunggah oleh
이희영Hak Cipta:
Format Tersedia
Thermal Strains and Element of the
Theory of Plasticity
Thermal Strains
Thermal strain is a special class of Elastic strain that
results from
expansion with increasing temperature, or
contraction with decreasing temperature
Increased temperature causes the atoms to vibrate by
large amount. In isotropic materials, the effect is the
same in all directions.
Over a limited range of temperatures, the thermal
strains at a given temperature T, can be assumed to be
proportional to the change, AT.
( ) ( ) T T T A = = o o c
0
(A8-1)
where T
0
is the reference temperature (c = 0 at T
0
). The
coefficient of thermal expansion, o, is seen to be in units
of 1/
o
C, thus making strain dimensionless.
Since uniform thermal strains occur in all directions in
isotropic material, Hookes law for 3-D can be
generalized to include thermal effects.
( ) | | ( ) T
E
z y x x
A + + = o o o v o c
1
( ) | | ( ) T
E
z x y y
A + + = o o o v o c
1
( ) | | ( ) T
E
y x z z
A + + = o o o v o c
1
(A8-2)
The theory of plasticity is concerned with a number of
different types of problems. It deals with the behavior
of metals at strains where Hookes law is no longer
valid.
From the viewpoint of design, plasticity is concerned
with predicting the safe limits for use of a material
under combined stresses. i.e., the maximum load which
can be applied to a body without causing:
Excessive Yielding
Flow
Fracture
Plasticity is also concerned with understanding the
mechanism of plastic deformation of metals.
Plastic deformation is not a reversible process, and
depends on the loading path by which the final state is
achieved.
In plastic deformation, there is no easily measured
constant relating stress to strain as with Youngs
modulus for elastic deformation.
The phenomena of strain hardening, plastic
anisotropy, elastic hysteresis, and Bauschinger effect
can not be treated easily without introducing
considerable mathematical complexity.
Figure 8-1(a). Typical true stress-strain curves for a ductile metal.
Hookes law is followed up to the yield stress o
0
, and beyond o
0
,
the metal deforms plastically.
Figure 8-1b. Same curve as 8-1a, except that it shows what happens
during unloading and reloading - Hysteresis. The curve will not be
exactly linear and parallel to the elastic portion of the curve.
Figure 8-1c. Same curve as 8-1a, but showing Bauschinger effect.
It is found that the yield stress in tension is greater than the yield
stress in compression.
Figure 8-2. Idealized flow curves. (a) Rigid ideal plastic material
Figure 8-2b. Ideal plastic material with elastic region
Figure 8-2c. Piecewise linear ( strain-hardening) material.
A true stress-strain curve is frequently called a flow
curve, because it gives the stress required to cause the
metal to flow plastically to any given strain.
The mathematical equation used to describe the stress-
strain relationship is a power expression of the form:
where K is the stress at c = 1.0 and n, the strain-
hardening coefficient, is the slope of a log-log of
Eq. 8-1
That is,
n
kc o =
(8-1)
c o log log log n K + =
(8-2)
FAILURE CRITERIA: FLOW/YIELD and FRACTURE
The Flow, Yield or Failure criterion must be in terms
of stress in such a way that it is valid for all states of
stress.
A given material may fail by either yielding or fracture
depending on its properties and the state of stress.
A number of different failure criteria are available,
some of which predict failure by yielding, and others
failure by fracture.
The terms flow criterion, yield criterion and failure
criterion have different meanings.
Yield criterion applies mainly to materials that are in
the annealed condition (usually ductile materials).
Failure criterion applies to both ductile and brittle
materials. However, it is mainly used for brittle
materials (fracture criterion), in which the limit of
elastic deformation coincides with failure.
Flow criterion applies to materials that have been
previously processed via work hardening (usually
ductile materials).
In applying a yielding criterion, the resistance of a
material is given by its yield strength.
In applying a fracture criterion, the ultimate tensile
strength is usually used.
Failure criterion for isotropic materials can be
expressed in the following mathematical form:
where failure (yielding or fracture) is predicted to occur
when a specific mathematical function f of the principal
normal stresses is equal to the failure strength of the
material, o
c
, from a uniaxial tension test.
( )
c
f o o o o =
3 2 1
, ,
(8-3)
The failure strength is either the yield strength o
o
, or the
ultimate strength o
u
, depending on whether yielding or
fracture is of interest.
Let us define an effective stress, o, which is a single
numerical value that characterizes the state of applied
stress. If
where o
c
is a known material property
Failure is not expected if
The safety factor against failure is given as:
That is the applied stress can be increased by a factor of
X before failure occurs.
) (
_
occurs failure
c
o o =
) (
_
failure no
c
o o <
_
o
o
c
X =
Maximum Normal Stress Criterion (Rankine)
Yielding (Plastic flow) takes place when the greatest
principal stress in a complex state of stress reaches the
flow stress in a uniaxial tension.
Since o
1
> o
2
> o
3
, Flow occurs when
o
0
(tension) = o
1
Compressive strength is usually greater than tensile
strength.
Flow stress in uniaxial tension
Maximum normal stress in a
complex stress state.
(8-4)
( ) ( ) n compressio tension
0 1 0
o o o < <
Where is the flow stress of the material.
The great weakness of this criterion is that it predicts plastic
flow of a material under a hydrostatic state of stress;
however, this is impossible, as shown by the example below.
It is well known that tiny shrimp can live at very
great depths. The hydrostatic pressure due to water is
equivalent to 1 atm (10
-5
N/m
-2
) for every 10 m; at 1000 m
below the surface the shrimp would be subjected to a
hydrostatic stress of 10
-7
N/m
-2
.
Hence,
0
o
2 7
3 2 1
/ 10 m N p = = = = o o o
Experiment to determine the yield stress of the shrimp
(defined as the stress at which the amplitude of the tail
wiggling would have becomes less than a critical value)
when crushed between two fingers showed that it occurred
at a stress of about 10
-5
N/m
-2
(14.5 psi).
Hence,
Rankines criterion predicts that shrimp failure would occur at
This corresponds to a depth of only 10m. Fortunately for all
lovers of crustaceans, this is not the case, and hydrostatic
stresses do not contribute to plastic flow.
2 5
0
/ 10 m N = o
2 5
0
/ 10 m N p = o
Maximum-Shear-Stress or Tresca Criterion
This yield criterion assumes that yielding occurs when
the maximum shear stress in a complex state of stress
equals the maximum shear stress at the onset of flow in
uniaxial-tension.
From Eq,(2.21), the maximum shear stress is given by:
Where is the algebraically largest and is the
algebraically smallest principal stress.
2
3 1
max
o o
t
=
(8.5)
1
o
3
o
For uniaxial tension, , and the maximum
shearing yield stress is given by:
Substituting in Eq. (8.3), we have
Therefore, the maximum-shear-stress criterion is given by:
0
3 2 , 0 1
= = = o o o o
0
t
2
0
0
o
t =
2 2
0
0
3 1
max
o
t
o o
t = =
=
0 3 1
o o o =
(8.6)
This criterion corresponds to taking the differences
between o
1
and o
3
and making it equal to the flow stress
in uniaxial tension.
This criterion does not predict failure under hydrostatic
stress, because we would have o
1
= o
3
= p and no
resulting shear stress.
von Mises or Distortion-Energy Criterion
This criterion is usually applied to ductile material
von Mises proposed that yielding would occur when
the second invariant of the stress deviator J
2
exceeds
some critical value.
where
for yielding in uniaxial tension
2
2
k J =
( ) ( ) ( ) | |
2
1 3
2
2 1
2
3 2 2
6
1
o o o o o o + + = J
0 ;
3 2 0 1
= = = o o o o
2 2
0
2
0
6k = + o o
(8.7)
Substituting Eq. 8-8 into 8-7, we obtain the usual form of
von Mises yield criterion. When the expression
then the material will flow. The above expression above is
known as effective stress. It is now accepted that it
expresses the critical value of the distortion (or shear)
component of the deformation energy of a body.
| |
o
o o o o o o o ) + +
2 / 1
2
1 3
2
3 2
2
2 1
) ( ) ( ) (
2
1
(8.9)
k 3
0
= o (8.8)
Additional Failure Criteria
Octahedral Shear Stress Yield Criteria: This is another
yield criteria often used for ductile metals. It states that
yielding occurs when the shear stress on the octahedral
planes reaches a critical value.
Mohr-Coulomb Failure Criterion: This is used for
brittle metals, and is a modified Tresca criterion.
Griffith Failure Criterion: Another criterion used for
brittle metals. It simply states that failure will occur
when the tensile stress tangential to an ellipsoidal cavity
and at the cavity surface reaches a critical level o
0
.
McClintock-Walsh Criterion: Another criterion used for
brittle metals. It is an extension of the Griffiths
criterion, and considers a frictional component acting on
the flaw faces that had to be overcome in order for them
to grow.
Example
A region on the surface of a 6061-T4 aluminum alloy
component has strain gage attached, which indicate the
following stresses:
o
11
= 70 MPa
o
22
= 120 MPa
o
12
= 60 MPa
Determine the yielding for both Trescas and von Mises
criteria, given that o
0
= 150 MPa (the yield stress).
Solution
Since we were given the value of o
12
, we must therefore
first establish the principal stresses. Invoke Eq. 4-37.
Hence,
o
1
= 160 MPa; o
2
= 30 MPa; o
1
= 0
According to Tresca, t
max
= (160 - 0)/2 = 80 MPa
For yielding in uniaxial tension:
o
0
/2 = 75 MPa
Since the 80 MPa > 75 MPa, Tresca criterion would be
unsafe.
|
|
.
|
\
|
+
|
.
|
\
|
+
=
2
12
2
22 11 22 11
2 1
2 2
, o
o o o o
o o
The von Mises criterion can be invoked from Eq. 8-9.
The L.H.S. of the above Eq. gives a value of 175 MPa.
This criterion predicts that the material will not fail (flow),
unlike the Tresca criterion, which predicts that the material
will flow.
Therefore, the Tresca criterion is more conservative than
the von Mises criterion in predicting failure.
| |
2 / 1
2
1 3
2
3 2
2
2 1
) ( ) ( ) (
2
1
o o o o o o o + + =
o
Anda mungkin juga menyukai
- Failure Theory For Piping MaterialDokumen29 halamanFailure Theory For Piping MaterialsaadvikhasBelum ada peringkat
- Tensile Testing of Ferrous and Non-Ferrous AlloyDokumen7 halamanTensile Testing of Ferrous and Non-Ferrous Alloyrama100% (1)
- Reference BooksDokumen23 halamanReference BooksIgor Gabriel Teixeira GómezBelum ada peringkat
- Yield Point PDFDokumen12 halamanYield Point PDFengineer bilal100% (1)
- Theories of Failure From My SOM BookDokumen17 halamanTheories of Failure From My SOM BookRavinder Antil89% (28)
- Failure Criteria PDFDokumen3 halamanFailure Criteria PDFShanBelum ada peringkat
- Johnson-Cook Empirical ModelsDokumen14 halamanJohnson-Cook Empirical ModelsSanaan Khan95% (21)
- Chap06 Mechanical BehaviorDokumen14 halamanChap06 Mechanical BehaviorAli khan7Belum ada peringkat
- Lecture 4C Failure Theory of Isotropic Materials From PopovDokumen13 halamanLecture 4C Failure Theory of Isotropic Materials From PopovJoshua KarthikBelum ada peringkat
- Mechanical Properties Guide for MaterialsDokumen55 halamanMechanical Properties Guide for MaterialsbinoBelum ada peringkat
- Study Note - Failure TheoriesDokumen9 halamanStudy Note - Failure TheoriesSboniso KhethukuthulaBelum ada peringkat
- Tensile Test of Brass SpecimenDokumen7 halamanTensile Test of Brass SpecimenmanmathkBelum ada peringkat
- Plasticity Theory Chapter on True Stress, Strain and Yield CriteriaDokumen24 halamanPlasticity Theory Chapter on True Stress, Strain and Yield CriteriaHakan Boyacı100% (1)
- Stress Strain CurveDokumen12 halamanStress Strain CurveGlerommie CastroBelum ada peringkat
- Yield Strength TestDokumen8 halamanYield Strength TestDr.L.V.PRASAD MeesaragandaBelum ada peringkat
- Theories of Failure2 PDFDokumen12 halamanTheories of Failure2 PDFDeepak AshokanBelum ada peringkat
- Solid Mechanics Ii BMCS 3333: Yield Criteria - Failure AnalysisDokumen42 halamanSolid Mechanics Ii BMCS 3333: Yield Criteria - Failure AnalysisaalijanaabBelum ada peringkat
- SAXSIM 2012 Plasticity JakelDokumen75 halamanSAXSIM 2012 Plasticity JakelHarsha KolarBelum ada peringkat
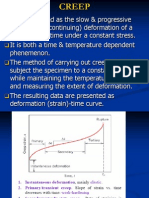
- Creep and FatigueDokumen20 halamanCreep and Fatiguecheveresan123100% (2)
- 17.creep & FatigueDokumen20 halaman17.creep & FatigueaderancBelum ada peringkat
- Yield (Engineering) PDFDokumen9 halamanYield (Engineering) PDFariyosageBelum ada peringkat
- Understanding Creep and Fatigue Deformation in MaterialsDokumen20 halamanUnderstanding Creep and Fatigue Deformation in Materialsgaspardo123Belum ada peringkat
- Tensile properties testing and stress-strain curvesDokumen4 halamanTensile properties testing and stress-strain curvesjontylee87Belum ada peringkat
- Theory of Plasticity: December 2018Dokumen28 halamanTheory of Plasticity: December 2018Angga Fajar SetiawanBelum ada peringkat
- PlasticityDokumen68 halamanPlasticitylram70100% (1)
- Theories of FailureDokumen77 halamanTheories of FailureAnonymous 6HADGUEXDBelum ada peringkat
- Principles of Metal Forming TheoryDokumen21 halamanPrinciples of Metal Forming TheoryAshok Kumar UppariBelum ada peringkat
- A Chapter6Dokumen28 halamanA Chapter6Faizan100% (1)
- Chapter 5: Failures Resulting From Static Loading: Failure of Truck Drive-Shaft Due To Corrosion FatigueDokumen20 halamanChapter 5: Failures Resulting From Static Loading: Failure of Truck Drive-Shaft Due To Corrosion FatigueDeepak AshokanBelum ada peringkat
- Chapter 3: Tensile TestingDokumen10 halamanChapter 3: Tensile TestingKhairul MuzafarBelum ada peringkat
- Design For Static LoadingDokumen18 halamanDesign For Static LoadingMohit SharmaBelum ada peringkat
- Obect:-Apparatus Required:: Practical No.1Dokumen5 halamanObect:-Apparatus Required:: Practical No.1mohammad_nizamaniBelum ada peringkat
- Yield Criteria PDFDokumen11 halamanYield Criteria PDFTarza Bayez100% (1)
- Theories of FailureDokumen13 halamanTheories of FailureDevansh SharmaBelum ada peringkat
- Mechanical Behavior of Materials: Tensile TestingDokumen34 halamanMechanical Behavior of Materials: Tensile TestingSebut Saja IrwanBelum ada peringkat
- Failure TheoriesDokumen47 halamanFailure TheoriesDeepak AshokanBelum ada peringkat
- Stress Concentration and FatigueDokumen22 halamanStress Concentration and FatiguelosoceBelum ada peringkat
- Tensile Testing Lab Determines Plastic PropertiesDokumen36 halamanTensile Testing Lab Determines Plastic PropertiesalkharfaneBelum ada peringkat
- Stress-Strain Diagram (Curve)Dokumen4 halamanStress-Strain Diagram (Curve)kevinBelum ada peringkat
- Deformation and Fracture Mechanics SolutionDokumen28 halamanDeformation and Fracture Mechanics SolutionSam Iguana100% (4)
- Mechanic FractureDokumen9 halamanMechanic Fracturehengki wibowoBelum ada peringkat
- Chapter 4Dokumen48 halamanChapter 4Zhiyi HeBelum ada peringkat
- Ch3. Stress and StrainsDokumen49 halamanCh3. Stress and StrainsAbimael wendimuBelum ada peringkat
- N.K. Sinha, J. Materials Sci., 23 (1988), P. 4415Dokumen14 halamanN.K. Sinha, J. Materials Sci., 23 (1988), P. 4415Universale EvileBelum ada peringkat
- Engineering Materials and Their Properties: - Significance ofDokumen53 halamanEngineering Materials and Their Properties: - Significance ofMisbah NiamatBelum ada peringkat
- Theories of Failure AnalysisDokumen27 halamanTheories of Failure Analysismuzamillover1Belum ada peringkat
- Experimental determination of crack softening characteristicsDokumen12 halamanExperimental determination of crack softening characteristicsDaniela Mihaiela BocaBelum ada peringkat
- Creep DescriptionDokumen11 halamanCreep DescriptionGerry AnandaBelum ada peringkat
- Material Science Unit 5 - Mechanical Properties of MaterialsDokumen31 halamanMaterial Science Unit 5 - Mechanical Properties of MaterialsJagdeep RahulBelum ada peringkat
- Mechanical Science for Technicians: Volume 1Dari EverandMechanical Science for Technicians: Volume 1Penilaian: 5 dari 5 bintang5/5 (1)
- The Mechanical Properties of Wood: Including a Discussion of the Factors Affecting the Mechanical Properties, and Methods of Timber TestingDari EverandThe Mechanical Properties of Wood: Including a Discussion of the Factors Affecting the Mechanical Properties, and Methods of Timber TestingBelum ada peringkat
- Strength of Materials and Structures: An Introduction to the Mechanics of Solids and StructuresDari EverandStrength of Materials and Structures: An Introduction to the Mechanics of Solids and StructuresPenilaian: 4 dari 5 bintang4/5 (1)
- Advanced Opensees Algorithms, Volume 1: Probability Analysis Of High Pier Cable-Stayed Bridge Under Multiple-Support Excitations, And LiquefactionDari EverandAdvanced Opensees Algorithms, Volume 1: Probability Analysis Of High Pier Cable-Stayed Bridge Under Multiple-Support Excitations, And LiquefactionBelum ada peringkat
- Solutions for Biot's Poroelastic Theory in Key Engineering Fields: Theory and ApplicationsDari EverandSolutions for Biot's Poroelastic Theory in Key Engineering Fields: Theory and ApplicationsBelum ada peringkat
- Hydrogen Production by Steam Reforming Chemical Engineering ProcessingDokumen8 halamanHydrogen Production by Steam Reforming Chemical Engineering ProcessingviettiennguyenBelum ada peringkat
- Air PollutionDokumen19 halamanAir PollutionMika Hakimie100% (1)
- C12HDokumen129 halamanC12Hkhudhayer1970Belum ada peringkat
- Chapter 2 - Analysis of Steam Power Plant CycleDokumen57 halamanChapter 2 - Analysis of Steam Power Plant Cycledmc constructionBelum ada peringkat
- Cascade Aeration Lecture 6 Environmental Engineering Unit Operations Spring 2014Dokumen16 halamanCascade Aeration Lecture 6 Environmental Engineering Unit Operations Spring 2014Song Nguyen NguyenBelum ada peringkat
- KinemaxDokumen2 halamanKinemaxJoe BloggsBelum ada peringkat
- Thermodynamics Lesson 2Dokumen12 halamanThermodynamics Lesson 2Lenard SusanoBelum ada peringkat
- CHROME STEEL SLEEVE Kavya Int Brochure PDFDokumen4 halamanCHROME STEEL SLEEVE Kavya Int Brochure PDFjoseluispaillachoBelum ada peringkat
- Determine Xenon's Ionization PotentialDokumen3 halamanDetermine Xenon's Ionization PotentialAbhi Rami50% (2)
- Standard M Ethods of Test For: Weight of Coating On Zinc-Coated (Galvanized) ) Iron or Steel ArticlesDokumen6 halamanStandard M Ethods of Test For: Weight of Coating On Zinc-Coated (Galvanized) ) Iron or Steel ArticlesRichard PalaciosBelum ada peringkat
- ADA Detectable Warning Plates - EJDokumen8 halamanADA Detectable Warning Plates - EJironworkBelum ada peringkat
- Unit III Engine Exhaust Emission ControlDokumen49 halamanUnit III Engine Exhaust Emission ControlMani Karthi100% (1)
- CESGas IncinerationDokumen21 halamanCESGas Incinerationsada sivaBelum ada peringkat
- 11 Chemistry Eng 2018Dokumen216 halaman11 Chemistry Eng 2018Deepanjali PalBelum ada peringkat
- MSCCH 506Dokumen176 halamanMSCCH 50620tamilselvi-ugcheBelum ada peringkat
- Application of CFD in Thermal Power Plants PDFDokumen4 halamanApplication of CFD in Thermal Power Plants PDFSylvesterBelum ada peringkat
- The Hydrobarrel: Designed and Built by Aaron SchadeDokumen16 halamanThe Hydrobarrel: Designed and Built by Aaron SchadeAaron SchadeBelum ada peringkat
- The Tensile-Yield Behavior ., of Ship'"S Ee.L: W: S. Owen, B, L Averbach and "Morris Coh&hDokumen45 halamanThe Tensile-Yield Behavior ., of Ship'"S Ee.L: W: S. Owen, B, L Averbach and "Morris Coh&hKaung Myat HeinBelum ada peringkat
- Fluid Mechanics Tutorial on Fluid Properties and CalculationsDokumen2 halamanFluid Mechanics Tutorial on Fluid Properties and CalculationsGabrielBelum ada peringkat
- Evaporation: Heat Transfer Coefficients and Single Effect EvaporatorsDokumen26 halamanEvaporation: Heat Transfer Coefficients and Single Effect EvaporatorsIram TahiraBelum ada peringkat
- Applied Quantum Mechanics: DR Uzma KhaliqueDokumen29 halamanApplied Quantum Mechanics: DR Uzma KhaliqueNaveed SultanBelum ada peringkat
- PhosphatingDokumen9 halamanPhosphatingnirai101259Belum ada peringkat
- Cswip 3 (1) .1 Bridge Examination QuestionDokumen3 halamanCswip 3 (1) .1 Bridge Examination QuestionbassamBelum ada peringkat
- Collision Theory Key ConceptsDokumen38 halamanCollision Theory Key ConceptsSaadiah MohammadBelum ada peringkat
- Extended Safety Data Sheet for Agidol-1Dokumen24 halamanExtended Safety Data Sheet for Agidol-1Sekawan CosmeticsBelum ada peringkat
- A Fixed-Bed Reactor Modeling Study On The Methanation of CO: Chemical Engineering Research and DesignDokumen11 halamanA Fixed-Bed Reactor Modeling Study On The Methanation of CO: Chemical Engineering Research and DesignJames LivingstonBelum ada peringkat
- An Overview of Traditional Fish Smoking in Africa PDFDokumen20 halamanAn Overview of Traditional Fish Smoking in Africa PDFBzmania SlimnzieBelum ada peringkat
- Acid and Base Number by Color-Indicator Titration: Standard Test Method ForDokumen7 halamanAcid and Base Number by Color-Indicator Titration: Standard Test Method ForLuis EnriqueBelum ada peringkat
- Adaptive Teaching Guide SampleDokumen2 halamanAdaptive Teaching Guide SampleMai SasaBelum ada peringkat
- Reinforcing Low-Grade Glulam Beams with GFRP RodsDokumen12 halamanReinforcing Low-Grade Glulam Beams with GFRP RodsCălin MartonBelum ada peringkat